重视课堂引入,实现有效教学

广东省佛山市华英学校

有效教学,就是在符合时代和个体积极价值建构的前提下其效率在一定时空内不低于平均水准的教学,有效教学的核心就是教学的效益.提高学生的学习能力,是有效教学的主要途径之一.学习,是指通过阅读、听讲、思考、研究、实践等途径获得知识或技能的过程,学习是认知的一种方式,通过对原有的认知结构对刺激物进行同化和顺应达到平衡的过程.所以,学习是在原有的认知上的再认知,原有的认知基础就是学习的元认知[1],元认知是指认知的认知.把握学习的元认知,在此基础上进行的教学,符合学生的学习特点与心理过程,达到有效教学.

数学教学内容指该内容在客观上所具备的数学含义,大体上可以分为概念意义上的,数学结构方面的,思想方法意义上的等等[2].区分不同的教学内容,研究每一节课学生的元认知,重视课堂引入,着眼于学生的最近发展区,引导学生有效学习,从而达到有效教学.

1 概念课的有效教学

数学概念是人脑对现实对象的数量关系和空间形式的本质特征的一种反映形式.正确地理解和形成一个数学概念,必须明确这个数学概念的内涵——对象的“质”的特征,及其外延——对象的“量”的范围.一般来说,数学概念是运用定义的形式来揭露其本质特征的.而一些原始数学概念,只能通过描述其特征得到概念.学生的认知总是依赖于对象的呈现方式与自身的元认知,在概念课教学时,教师需要认真研究概念的本源,从根本上把握概念,寻求恰当的引入方式.下文以北师大版的七年级下册第四章第一节“认知三角形”为例,说明如何根据学生的元认知,设计引入方式,达到有效教学.

“认知三角形”是新授课,学生的元认知有点、线、面、体,以及角,这节课的难点是三角形概念的提出,学生理解三角形的方式,会影响以后对其他几何知识的学习模式.

引入1请画几个三角形,试一试,描述你的画法.

设计意图:学生在小学阶段了解过三角形,并懂得三角形的形状,这节课是再认知,唤醒元认知是必要环节,唤醒方式有不同,可以通过观看图片,但动手操作是最直接和接近三角形本质特征的,减少对概念理解的干扰.描述画法,实际上就是对三角形概念的提炼,根据学生自身的元认知进行认知,能够有效教学.只要学生对概念的描述符合本质特征的,都可认为是正确的,也应该是正确的,比如“依次连接不共线的三点所形成的图形是三角形”等.

引入2观察自己画的三角形,想一想,你能够找到哪些你认识的几何量,比如点、线段之类的?这些几何量内部之间有什么关系吗?试着描述出来.

设计意图:充分利用学生的元认知进行再认知,使得认知是“自然”的.在学生的认知基础上提炼出三角形的要素,并对要素之间的关系进行探究.这种学习方式,实际上就是几何图形的研究方式,需要在平时教学中渗透数学的研究方法,提高学生学习能力.

2 数学结构课的有效教学

结构是概念与概念之间通过某种媒介进行关联从而形成一个整体,数学结构方面的内容包括几何公理和定理,变量间关系等等.学生在数学结构的学习中,元认知起到非常重要的作用.下文以北师大版的八年级上册第一章第一节“探索勾股定理”为例,说明如何利用元认知的方法实施有效教学.

“第一节探索勾股定理”是新授课,属于数学结构方面上的知识.学习勾股定理的前置知识有直角三角形的定义,一元一次方程的解法,整式的运算,正方形与直角三角形的面积公式等等.这些都属于这节课的元认知,在新授课之前,可以进行简短的回忆与梳理.“勾股定理的三边关系是如何引导出来的”是本节课的难点,这是新的认知,需要“定量且必需的材料”刺激才能进行认知和学习.教材的引入与引导非常直接,让学生进行边平方的计算,然后直接验算较短边的平方和与最长边的平方之间是否相等,这种方法只会让学生知其然而不知其所以然.格式塔心理学家认为,通过对问题情境的内在性质有所顿悟的方式来解决问题,就可以避免与这一问题情境不相干的大量随机的、盲目的行动,而且有利于把学习所得迁移到新的问题情境中去.勾股定理的核心是边的平方,平方给与学生的反应是正方形的面积,所以通过设计正方形的面积,引导学生观察,发现直角三角形的三边平方之间的关系,是符合认知原理的.下面是本人的引入设计:

引入3观察下图1-3,每个虚线小方格的边长为1,试一试求出每个正方形ABCD的面积.

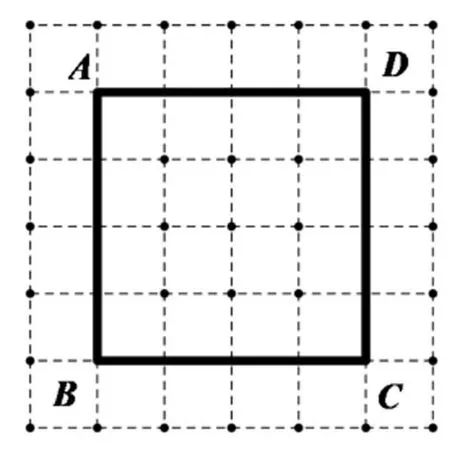
图1

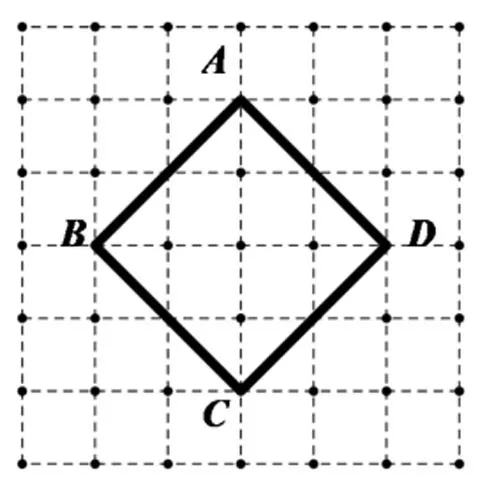
图2

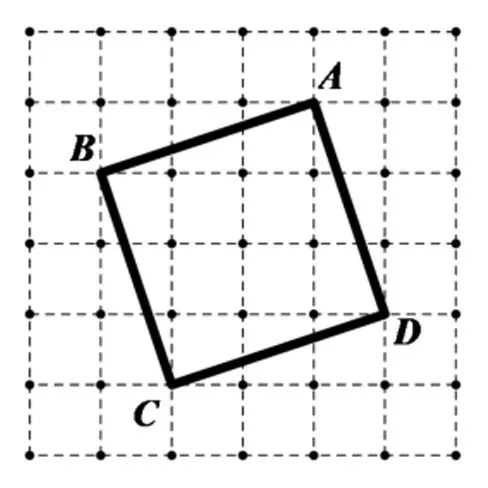
图3

设计意图:图1的正方形面积是显然的,目的是引起学生的回忆;图2的正方形的面积有一定难度,无法直接求得,需要学生做一些辅助线,这是引入的目的,引发学生的思考,如何求面积,引出学生对正方形进行割补;图3是图2正方形的一般化,让学生对图2的割补法进行一般化,说明这种方法具有一般性.

对图3的割补情况进行汇总,有如下两种主要方式:

图4

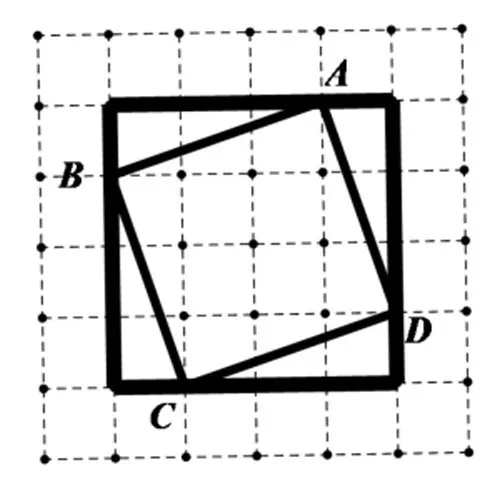
图5

让学生尝试求解,然后提出思考:

任选其中上图的一种图形,画出一般化的图形如图6-7,探索直角三角形、小正方形、大正方形的面积之间有什么样的联系,如何用符号表示?

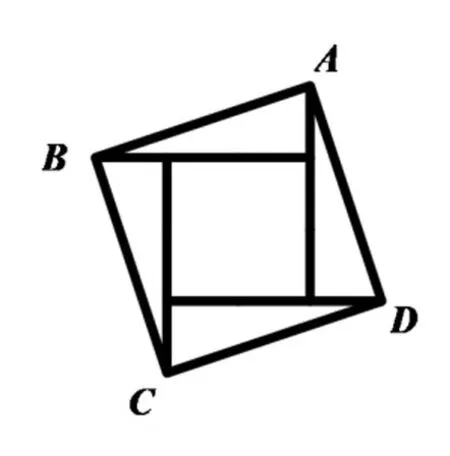
图6

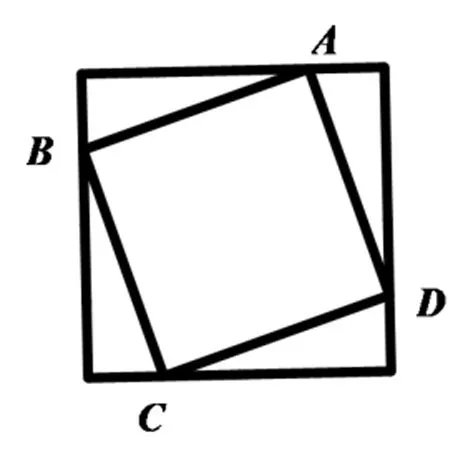
图7

学生的尝试实际上就是勾股定理的证明过程.

对比课本的引入,上述方法避免了在学生的认知上生硬的介入,充分重视学生的元认知,强调认知是元认知上的再认知,符合学生的认知规律,达到有效教学的目的.

3 思想方法课的有效教学

数学思想方法课主要是指如何运用学过的数学知识解决具体问题的课程教学,这种课堂教学过程包括问题提出、模型建立、模型求解、下结论等过程.学生在认知过程中,属于元认知的有各种数学模型的求解,难点在于模型建立.下文以北师大版的八年级上册第一章第三节《勾股定理的应用》为例,说明如何利用元认知的方法实施有效教学.

引入4如图8-10,在一个圆柱的表面上有两点A和B,沿着圆柱的侧面从A到B画一条线,如何画,才能使得这条线最短?

1.如图8,点A与B在同一个底面的圆周上;

2.如图9,点A与B都在侧面上;

3.如图10,点A在侧面上,点B在底面圆周上;

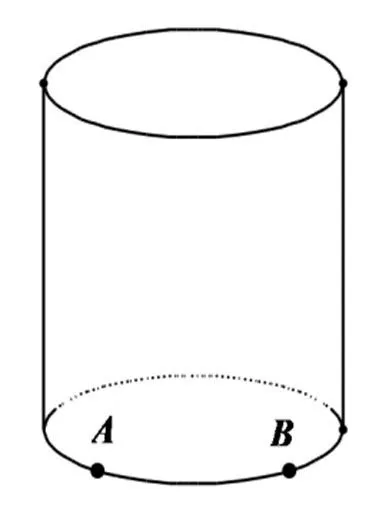
图8

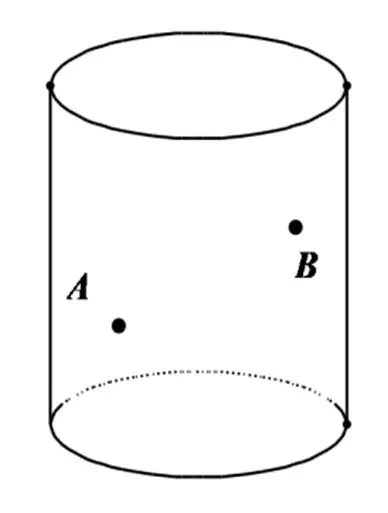
图9

图10

设计意图:图8的作用是唤醒学生的元认知,“两点之间,线段最短”是这种题目解决的依据;图9-10是学生认知的难点,图9 如何画线才能最短,学生会根据自身的元认知,想到构造“平面”,利用“两点之间,线段最短”,从而自然的引出需要画出圆柱侧面展开图.

学生第一次学习“几何体表面最短路径问题”,需要从本质上理解为什么需要通过侧面展开图利用“两点之间,线段最短”来建立模型.

数学思想方法课的教学,强调引入,讲究点到为止,忌讳教师全包干,留有余地让学生思考,让学生体会为何如此建模,从而达到有效教学的目的.

4 结束语

学生的元认知体系是不断发展的,新学习的知识,是下一次学习的元认知.教学方法很多,有效教学是唯一目的,基于学生的元认知,重视课堂引入,实现有效教学.