在递进式问题中促进数学思维自然生长*——以“三角形中位线定理证明”教学为例

华南师范大学附属南沙中学广州市冯少勤名师工作室

教学内容安排在人教版八年级下册第十八章“平行四边形”,目标定位是理解利用平行四边形性质分析三角形中位线性质的合理性,掌握三角形中位线定理的证明,从中渗透转化思想,培养数学建模、数学抽象以及逻辑推理的核心素养.以下设计仅对定理证明的教学进行设计,呈现主要环节和意图,探索如何突破添加辅助线证明的难点,并提出三点教学思考.

1 设计简案

环节1 回顾定理

问题1:何为三角形中位线?中位线定理内容是什么?

设计意图:教师提出问题,学生回答问题.直截了当回顾旧知,明确研究对象,理清证明目标:两条线段的位置关系与数量关系.

环节2 获得思路

问题2:如何证明三角形的中位线定理?从定理的结论出发,显然是两条线段的位置关系以及数量关系,证明两线平行的方法一般有哪些?证明两线相等的方法一般有哪些?这些方法可行吗?

追问1:有没有一个方法既涉及到两条线段的位置关系又涉及到数量关系?之前知识是否学到类似的结论?

追问2:构造平行四边形,用平行四边形的性质证明三角形的中位线性质,有无它的合理性?你是如何理解的?

设计意图:从问题入手,挖掘已有的证明经验,激发思维,寻求方法,筛选方法.通过问题导向和追问思维,师生共同梳理方法,形成观念:通过三角形的全等研究平行四边形性质,反过来,也可通过平行四边形性质获得中位线性质.并形成图1的证明思维导图,旨在通过对知识寻根问源,回顾平行四边形性质的获得过程帮助学生理解构造平行四边形的合理性,对比两个结论的求证路径找到可行的方法,理解证明思路的来源,初步感知证明思路的切入口:添加辅助线构造新的图形.

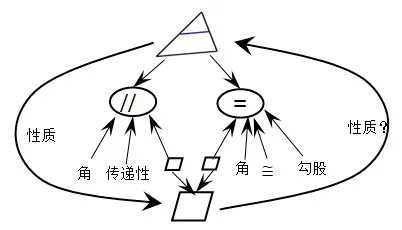
图1

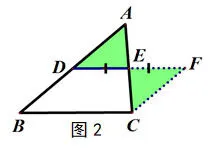
学生初步尝试,得证明方法1(图2):延长DE到点F,使得DE=EF,连接CF.(或者再分别连接DC、AF)

环节3 拓宽思路

该环节呈现教学实录片段:

师:刚才的这种方法,如何添加辅助线实现线段倍长?还有其它考虑方向实现倍长吗?

生:他是通过补长DE来实现的,应该还可以通过截BC来实现.

师:对!那如何通过补或截来实现位置关系的证明?需要构造一个什么新的图形?这个新的图形的构造是随意的吗?构造时它的边长最好是哪些边?

生:通过构造一个平行四边形,这个平行四边形不是随意构造的,它的边长最好是两条目标线段为边长,即可以考虑:以DE为边长的平行四边形,或者以BC为边长的平行四边形.

师:基于以上分析,还有其它证明方法吗?请小组协作寻找新的证明方法.

设计意图:以一种方法为跳板,通过深度剖析证明的思路以及涉及的思想方法,帮助学生形成模型,突破数学抽象.再通过后续的小组共同协作,利用新得到的工具重新解决问题,以达到知识的迁移与创新.

环节4 再用思路

小组代表展示各种证明思路:

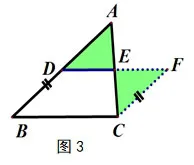
证法2(图3):过点C作AB的平行线CF,交DE延长线于点F.

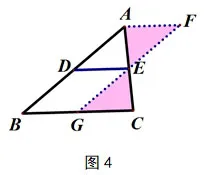
证法3(图4):过点E作AB的平行线EF,交BC于点G,过点A作BC的平行线AF,交GE于F.

设计意图:呈现一般的证明方法,并对方法进行分析总结:证法2 用了补DE的方法,证法3 用了截BC的方法,其中证法1、2、3 都是用一个中点同侧进行补短或截长构造平行四边形.基于总结顺应思维提出思考:可以考虑利用两个中点向两侧来补短或截长吗?让学生尝试得出如下更一般的证法,从证法2、3到证法4、5 体现了从特殊到一般的证明思路和研究方法,符合认知规律.

可让学生课后完成:

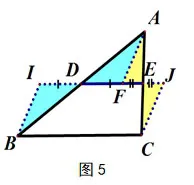
证法4(图5):在线段DE上任意取一点F,延长FD于点I,使得DF=DI,延长FE于点J,使得EJ=EF,连接BI,AF,CJ.

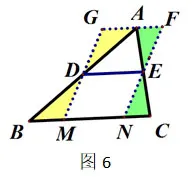
证法5(图6):在BC上任取一点M,过点E作DM的平行线EN交BC于点N,过点A作BC的平行线AG,交DM于点G,交EN于点F.

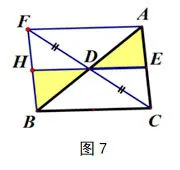
证法6(图7):连接CD,并延长CD于点F,使得DF=CD,连接AF,BF,BF交ED于点H.

环节5 总结提炼

问题3:经历了刚才的证明你获得了哪些数学思想方法?观察各种证法的图形,你发现了三角形与平行四边形有什么特殊的联系?譬如它们之间如何转换?

小结:事实上,任何一个三角形都能通过中位线的图形变换割补成一个与之面积相等的平行四边形,反过来,任何一个平行四边形都能恒等变换成与之面积相等的三角形,所以平行四边形的问题我们可以用三角形来解决,三角形的问题也可以用平行四边形的相关知识来突破.

设计意图:梳理知识,升华思想,掌握方法,发现规律,创新认知.

2 教学思考

2.1 理解教材

三角形中位线是平行四边形性质、判定之后的一个推论,结论含有两条线段的位置关系与数量关系,是四边形、三角形的有关证明以及计算的重要定理.对三角形中位线的研究,体现了三角形、四边形相关知识系统的统一性;同时中位线的定理证明涉及到很多数学思考与思想方法,其数学学科的内涵价值高,此为学生提高分析问题、解决问题的能力提供了丰富的素材.

2.2 理解学生

学生此前已经掌握了全等三角形、利用全等三角形探索得到平行四边形的性质和判定.具有研究四边形问题时会转化成三角形问题研究的意识和一定的研究经验,以及一定的逻辑推理能力.当然,也存在一些不利的教学因素.其一,中位线的定理的证明思路多种多样,如何基于学生已有的证明经验梳理出可行的证明方法,是个难点;其二,定理的原几何图形简单,涉及的两个结论需要学生构造新的图形(全等三角形、平行四边形),构造的关键是如何利用两个中点添加辅助线,这是学生的另一个难点.

2.3 理解教学

教学应以培养学生的核心素养为本源,因此,需要注重通过问题导向,在数学活动中引入数学思考以发展思维能力.从证明思路的获得上引导学生尝试用平行四边形的方法证明结论,通过不同方法的截长补短获得证明思路的多样性,能从分析问题解决问题的过程中渗透数学转化、从特殊到一般的思想,并关注数学建模以及逻辑推理、数学抽象的核心素养的养成.同时,顺应学生思维,通过对整堂课的小结,带领学生反思、揭示三角形与平行四边形整体架构,强化了两个内容的系统统一性.

教学应以思维发生的载体而生长深入,因此考虑如何基于学生已有的证明经验梳理出可行的证明方法?采取的是抛开脚手架,从认知的一般情况入手,模拟遇到问题的第一反应:寻求方法解决问题.通过问题导向,调动学生已有的证明经验,挖掘出能够可行的素材,通过思维导图的呈现,帮助学生梳理出证明的优解:构造平行四边形,虽然这种处理方法学生不太容易获得思路,但是此种方法符合学生遇到问题的真实情况,思维的活动更活跃更灵动,也为学生今后分析问题解决问题提供了示范.

教学应以思路拓宽而形成能力,因此考虑到添加辅助线的多样性、抽象性和不确定性,学生的数学建模能力以及图形直观素养尚在较低水平,思维的深广度尚不能独立解决问题.为此,在得到一种证明方法后,不急于展示其它方法,而以此为蓝本,进行方法的深度透析,通过问题导向,把需要构造的平行四边形定性:通过截长补短构造以目标线段DE或者BC为边长的平行四边形,获得此认知后让学生尝试考虑其他证明方法,同时拓宽思维:利用一个中点截长补短;利用两个中点截长补短,渗透从特殊到一般的研究方向,这样处理不会一下子拔得太高,让学生先感悟了理解了方法,才能更好的使用方法,从而提升学生对证明思路的发散度和思维超越,以达到知识迁移以及知识的创新.

2.4 理解数学

教师的教法和学生的学法离不开数学理解,数学知识是个整体,整体中的每一部分又相互联系,因此,在教学中关注数学知识整体和联系的学习至关重要.有三点需要理解清晰.

一是思路为什么这样来?需要理解数学知识的来龙去脉.基于学生已学的知识和方法经验,引导学生对知识寻根问源,通过回顾平行四边形的性质的获得过程以及平行四边形对边的性质理解构造平行四边形的合理性,对证明方法进行梳理和呈现思维导图,让知识方法来得自然、合理、有据,解决了知识怎么来的问题.

二是知识去哪儿,怎么去?在获得第一种证明方法后,从方法的特征中深度解剖证明的思路,通过问题串的引导以及小组协作完成任务单以突破其他添加辅助线的方法,拓宽学生的思维,提升学生对性质证明思路的发散度和思维超越,以达到知识迁移以及知识的创新,从而达到分析问题解决问题的能力的培养,解决了知识怎么去的问题.而通过对比各种证明思路以及方法,对比各种证明方法的图形,发现图形的相互转化,发现三角形与平行四边形之间面积恒等与方法互动的创新结论,解决知识去哪里的问题.

三是整体和联系的学科价值观如何呈现?课最后的小结内容,基于三角形与平行四边形的性质转化,转化的着重点是本节课的证明过程与研究方法,并在此基础上增加了图形之间的定性转化,通过对比各个证明图形的切割与合成,学生不难发现三角形与平行四边形在形状上是可以相互转化,任何一个三角形都可以通过中位线的切割变换成与之面积相等的平行四边形,反之亦然.这深刻体现了我国《九章算术》中的出入相补转化思想,此结论的获得使得课堂更具有人文味,内涵更丰富.

3 结束语

核心素养中提到关键能力,它体现在知识学习的三种形态:知识的理解,迁移以及创新,简单概括就是指数学的思维和方法的理解和迁移应用.如何基于学生已有的知识设置教学活动引入数学思考,从数学活动中获得素养的养成,最佳的方法莫过于学生的经历与体验感悟,思维的产生也必然是顺应学生的已有认知进而产生拓展的,教师要利用好教学的载体,通过引导分析,对比,归纳,以问促思,拓宽思维的发散度以及加深思维的深刻性.