如何提高数学阅读能力

杨会涛　胡志奇

【摘 要】 近些年，高考中的概率统计试题越来越加强对数学阅读能力的考查，我们如何帮助学生了解和提升数学阅读能力呢？ 这是每个一线教师关心的问题，笔者以2019年高考数学理科全国Ⅰ卷概率统计解答题为例，研究了数学阅读（能力）的内涵以及提升数学阅读能力的途径，在这个过程中有了一些粗浅的认识，希望这些想法能够帮助学生从容应对高考中的概率统计试题.

【关键词】 数学阅读;数学阅读能力;概率统计

2017年、2018年、2019年全国Ⅰ卷理科数学中，概率统计解答题分别位于19、20、21题的位置，尤其是2019年，它取代了导数试题而成为压轴题.2018年，教育部考试中心任子朝、陈昂、赵轩联合在《数学通报》发表署名文章《加强数学阅读能力的考查 展现逻辑思维功底》，文章指出：“近年概率与统计试题得分不高的原因可以归结为试题联系实际并不是以考生熟悉的形式呈现，运算量比较大，但最重要的原因是学生读不懂试题，不能理解题意，所以没有解题基础，因此从本题看数学阅读能力是解决问题的关键[1].”

试题中的数学阅读就是要求考生能够根据数学问题仔细地理解题意，明白题目的要求，进而准确地制定出解决问题的方案.在这个过程中，我们需要借助已经掌握的基本知识、基本技能、基本思想和基本活动经验（简称“四基”[2]）来理解和运用数学语言，由于数学语言与社会科学语言不同，它主要包含三种语言（文字语言、符号语言和图表语言），其中符号语言带来的抽象性决定了数学阅读不同于语文、英语等其他阅读[3].数学阅读能力主要包括：准确理解原文，较快的阅读速度，发现和提出问题的能力、分析和解决问题的能力[4]（简称“四能”[2]）.下面我们就以2019年全国Ⅰ卷理科数学压轴题为例，谈一谈数学阅读的主要步骤以及提高数学阅读能力的途径.

1 试题再现

（2019全国卷Ⅰ理21）为了治疗某种疾病，研制了甲、乙两种新药，希望知道哪种新药更有效，为此进行动物试验.试验方案如下：每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠，随机选一只施以甲药，另一只施以乙药.一轮的治疗结果得出后，再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时，就停止试验，并认为治愈只数多的药更有效.为了方便描述问题，约定：对于每轮试验，若施以甲药的白鼠治愈且施以乙药的白鼠未治愈，则甲药得1分，乙药得-1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈，则乙药得1分，甲药得-1分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β，一轮试验中甲药的得分记为X.

（1）求X的分布列;

（2）若甲药、乙药在试验开始时都赋予4分，pi（i=0，1，…，8）表示“甲药的累计得分为i时，最终认为甲药比乙药更有效”的概率，则p0=0，p8=1，pi=api-1+bpi+cpi+1（i=1，2，…，7），其中a=P（X=-1），b=P（X=0），c=P（X=1）.假设α=0.5，β=0.8.

（ⅰ）证明：{pi+1-pi}（i=0，1，2，…，7）为等比数列;

（ⅱ）求p4，并根据p4的值解释这种试验方案的合理性.

2 试题解析（主要步骤）

2.1 粗读

就是大致的把本题浏览一遍，在浏览的过程中坚持不添字、不漏字[5]，通过感知题中的数学语言，认识和了解到本题是一道概率与数列相结合的试题，重点记住试题的要求：“求一轮试验中甲药的得分X的分布列？”;“证明{pi+1-pi}（i=0，1，2，…，7）为等比数列并求p4？”

2.2 圈读

对于问题（1），我们可以去研究试验“约定”的内容，必要时可以圈圈画画，“约定”内容的意思是“在一轮试验中，如果使用甲没有治愈白鼠，而使用乙药治愈了白鼠，那么X=-1;如果使用甲乙两种药都治愈或都未治愈白鼠，那么X=0;如果使用甲治愈了白鼠，而使用乙没有治愈白鼠，则X=1.”因此X=-1，0，1，

P（X=-1）=（1-α）β，P（X=0）=αβ+（1-α）（1-β），P（X=-1）=α（1-β），则X的分布列如下：

对于问题（2）中的第（ⅰ）问，我们可以直接利用“p0=0，p8=1，pi=api-1+bpi+cpi+1（i=1，2，…，7），其中a=P（X=-1），b=P（X=0），c=P（X=1）.假設α=0.5，β=0.8”去推导.由于问题是“证明{pi+1-pi

}（i=0，1，2，…，7）为等比数列并求p4？”我们只需要快速准确地计算出a，b，c的值并代入“pi=api-1+bpi+cpi+1”即可，并不用去理解“pi=api-1+bpi+cpi+1”是怎么得到的，（这个式子是利用全概率公式推导出来的，大家可以试一试.）我们只需要会用就可以.此时，由（1）知，a=P（X=-1）=（1-0.5）×0.8=0.4，b=P（X=0）=0.5×0.8+（1-0.5）（1-0.8）=0.5，c=P（X=1）=0.5×（1-0.8）=0.1.

所以pi=0.4pi-1+0.5pi+0.1pi+1，即pi+1=5pi-4pi-1，所以pi+1-pi=4（pi-pi-1），显然p1-p0=p1≠0（若p1-p0=p1=0，则pi+1=pi，进而p8=p7=…=p1=0与p8=1矛盾）.所以数列{pi+1-pi}（i=0，1，2，…，7）是以p1为首项，公比为4的等比数列.

（ⅱ）由（ⅰ）知pi+1-pi=p1×4i，所以p1-p0=p1×40，p2-p1=p1×41，…，p8-p7=p1×47，利用迭加法知：p8-p0=p1×（40+41+…+47）=48-13p1=1，则p1=348-1.

p4=p4-p0=p1×（40+41+42+43）=348-1×1-441-4=144+1=1257≈0.0039.我们如何根据p4≈0.0039去解释这个方案的合理性呢？虽然离成功只有一步之遥，但这一步是何等的艰辛啊！

2.3 精读

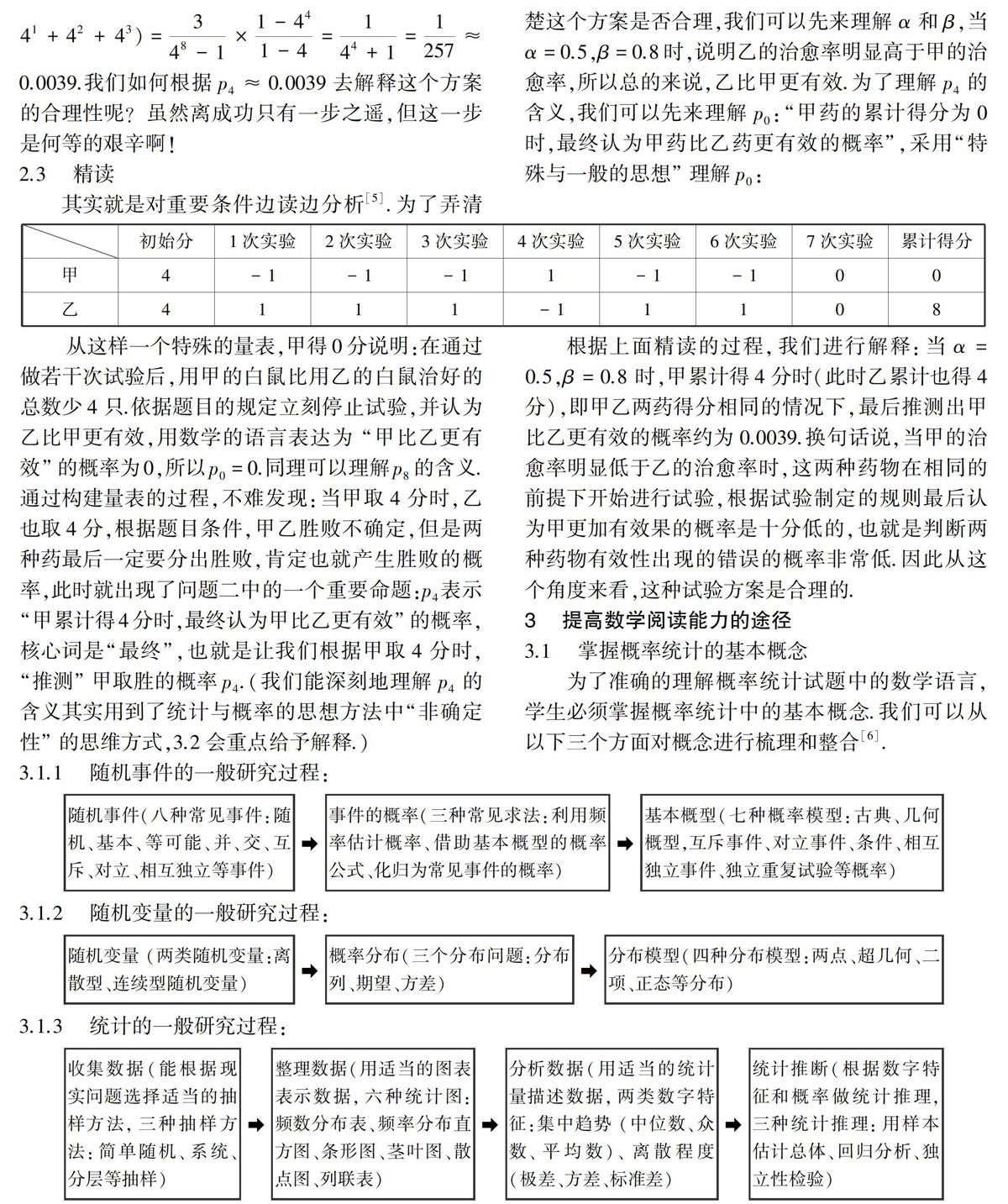
其实就是对重要条件边读边分析[5].为了弄清楚这个方案是否合理，我们可以先来理解α和β，当α=0.5，β=0.8时，说明乙的治愈率明显高于甲的治愈率，所以总的来说，乙比甲更有效.为了理解p4的含义，我们可以先来理解p0：“甲药的累计得分为0时，最终认为甲药比乙药更有效的概率”，采用“特殊与一般的思想”理解p0：

从这样一个特殊的量表，甲得0分说明：在通过做若干次试验后，用甲的白鼠比用乙的白鼠治好的总数少4只.依据题目的规定立刻停止试验，并认为乙比甲更有效，用数学的语言表达为 “甲比乙更有效”的概率为0，所以p0=0.同理可以理解p8的含义.通过构建量表的过程，不难发现：当甲取4分时，乙也取4分，根据题目条件，甲乙胜败不确定，但是两种药最后一定要分出胜败，肯定也就产生胜败的概率，此时就出现了问题二中的一个重要命题：p4 表示“甲累计得4分时，最终认为甲比乙更有效”的概率，核心词是“最终”，也就是让我们根据甲取4分时，“推测”甲取胜的概率p4 .（我们能深刻地理解p4的含义其实用到了统计与概率的思想方法中“非确定性”的思维方式，3.2会重点给予解释.）

根据上面精读的过程，我们进行解释：当α=0.5，β=0.8 时，甲累计得4分时（此时乙累计也得4分），即甲乙两药得分相同的情况下，最后推测出甲比乙更有效的概率约为0.0039.换句话说，当甲的治愈率明显低于乙的治愈率时，这两种药物在相同的前提下开始进行试验，根据试验制定的规则最后认为甲更加有效果的概率是十分低的，也就是判断两种药物有效性出现的错误的概率非常低.因此从这个角度来看，这种试验方案是合理的.

3 提高数学阅读能力的途径

3.1 掌握概率统计的基本概念

为了准确的理解概率统计试题中的数学语言，学生必须掌握概率统计中的基本概念.我们可以从以下三个方面对概念进行梳理和整合[6].

3.1.1 随机事件的一般研究过程：

3.1.2 随机变量的一般研究过程：

3.1.3 统计的一般研究过程：

掌握以上基本概念为我们把实际问题转化为数学问题提供了关键依据，例如在2018年高考全国Ⅰ卷理数第20题中，通过“先从这箱产品中任取20件作检验”和“设每件产品为不合格品的概率都为p（0

3.2 掌握统计与概率的思想方法

《2019年考试大纲的说明》中把统计与概率的思想[7]作为六大数学思想方法之一.因为统计与概率研究的是非确定性的随机现象，它属于非确定性数学的范畴[8]，所以造成学生不太好掌握统计与概率的思想.学生更喜欢解决确定性数学的试题，一看到概率统计试题“脑子里缺了一根弦儿[9]”.比如在认识和理解p4的过程中，我们相信学生很容易理解p0和p8的含义，它们属于确定性数学的范畴，而甲取i（i=1，2，3，…，7）分时，根据题目条件，甲乙胜败不能确定，但是两种药最后一定要分出胜败，肯定也就产生胜败的概率，此时就出现了问题二中的一个核心词 “最终”，也就是让我们根据甲取i分时，“推测”甲取胜的概率pi .再比如2016年试题是“以购买易损零件所需费用的期望值为决策依据，在n=19与n=20之中选其一， 应选用哪个？”;2017年试题是“（Ⅰ）试说明上述监控生产过程方法的合理性;”这些问题都涉及到 “非确定性”的思考方式.因此掌握统计与概率的思想方法是学生提升数学阅读能力的关键.

3.3 掌握数学语言的阅读策略

3.3.1 文字语言

如果我们掌握了概率统计的基本概念，那么很容易理解文字语言的含义.但是，由于试题文字表述的简洁性，我们必须理清一些关键词、关键语句的内涵.比如2017年试题：“根据长期生产经验，可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N（μ，σ2）”，指的是“每個”零件的尺寸服从正态分布N（μ，σ2）;2018年试题：“如检验出不合格品，则更换为合格品”和“已知每件产品的检验费用为2元，若有不合格品进入用户手中，则工厂要对每件不合格品支付25元的赔偿费用.”两句文字表述放到一起理解：如果厂子进行检查，只需要支付每件2元的检查费，那么到用户手中都是合格产品;如果厂子不进行检查，若存在不合格产品流入用户的手里，则厂子要承担每件不合格产品25元的赔偿费.

3.3.2 图表语言

2018年、2019年试题中没有图表，2016年试题中有频数图，2017年试题中有统计表.对于图表的阅读，我们可以先读表头再读数据，文字图表相结合，表头与数据相对应.逐行逐列认真阅读的同时，还要认真思考问题与图表的关系、问题与数据的关系，根据这些关系确定出解题策略[10].

3.3.3 符号语言

符号语言是一种抽象而又简洁的数学语言.有时我们只需要会用它就可以了，而不必知道它的内涵，比如“pi=api-1+bpi+cpi+1（i=1，2，…，7）”.但有时，我们必须搞清楚它的含义，比如“p4”的含义.我们如何判断“符号语言”在一道试题中的要求层次呢？这需要借助下面的阅读技巧.

3.4 正确运用阅读技巧

在阅读试题时，为了快速准确制定出解题方案，我们需要坚持粗读（感知试题的知识框架，明确问题的要求.）→圈读（带着问题有选择的去阅读.）→精读（对于较复杂的问题不能跳跃性的阅读，需要手脑并用，对材料中的每个字、每个公式都要注意到.）.其实在经历“粗读”、“圈读”之后，我们可以快速准确地判断出“符号语言”的要求层次，同时对于很多试题，我们在完成“粗读”和“圈读”之后，都能够制定出解题方案，但较复杂的试题，只有在进行精读完以后才能够制定出最后的解题方案.

总之，提高数学阅读能力，可以帮助我们快速准确地制定出解题方案.但是想要得到正确的答案，还需要学生在平时培养自己的数据分析和数学运算的能力.另外，学生要加强对往年高考试题的研究，利用阅读策略和技巧发现命题的特点，找出命题的规律，最终能够从容应对概率统计解答题.

参考文献

[1] 任子朝，陈昂，赵轩.加强数学阅读能力的考查 展现逻辑思维功底[J].数学通报，2018，57（7）：8-13.

[2] 中华人民共和国教育部.普通高中数学课程标准[M].北京：人民教育出版社，2017.

[3] 仲爱云.数学阅读研究概述[J].教学与管理，2009（6）：88-90.

[4] 田园.加强中学生数学阅读能力的培养[J].数学通报，2013，52（6）：9-11.

[5] 孙鸣霞.数学教学应重视培养学生的阅读能力[J].教学与管理，2016（1）：33-34.

[6] 庞新军，邓春源.2017年高考全国I卷概率统计解答题评析[J].中学数学研究，2017（9）上：14-17.

[7] 教育部考试中心.2019年普通高等学校招生全国统一考试大纲的说明（理科）[M].北京：高等教育出版社，2018.

[8] 史宁中.数形结合与数学模型[M].北京：高等教育出版社，2018.

[9] 王芝平，张唯一，李振雷.2019年高考全国Ⅰ卷理科概率问题的解析与背景[J].数学通报，2019，58（8）：55-57.

[10] 韦力慧.浅谈学生數学阅读能力的培养[J].教育理论与实践，2014，34（29）：58-59.

作者简介

杨会涛，高级教师，邢台市第二中学数学教研室主任，河北省优秀教师，河北省“三三三人才工程”第三层次人选，河北省名师工作室成员，河北省基础教育工作专家库成员，河北省高中数学优质课一等奖获得者，主持并完成河北省“十一五”规划课题《新课程标准下高中数学教学模式创新的研究》，在省级及以上期刊发表多篇论文.

胡志奇，一级教师，邢台市普通教育教学研究室教研员，在核心期刊《数学教育学报》发表《数学教师素质结构的实证研究》.