调和映照的正规性
2020-06-03 02:28孙乾乾陈行堤胡春英
华侨大学学报(自然科学版) 2020年3期
孙乾乾, 陈行堤, 胡春英
(华侨大学 数学科学学院, 福建 泉州 362021)
1 预备知识





Arbelaez等[3]给出正规调和映照的一个判别定理.



其中,Ik的递推公式为



设z1,z2是区域Ω内的任意两点,记l(γ)为连接z1,z2的任意可求长曲线的长度.若存在常数1≤M<+∞,使得l(γ)≤M|z1-z2|,则称Ω为M-线性连结区域[11].
2 主要结论与证明


则fuα(z)是正规的.
证明: 假设‖fuα‖n<+∞,∀z,w∈D,γ:[0,1]→D是连结z,w的双曲测地线,则有


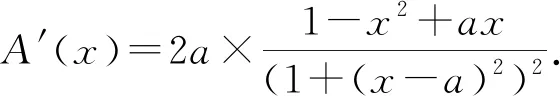

因此,A(x)在[0,+∞)内有上界.

证明:假设f(z)是正规的.由定理A得
又由定理B得

从而有
因为g(z)∈B1,所以有
所以有如下两种情况.
1) 当|f(z)| 2) 当|f(z)|≥B1时,由引理1可得 所以有 故fu1(z)是正规的. 由g(z)∈B1当且仅当g′(z)∈B2,利用递推知g(α)(z)∈Bα+1.从而由命题1可得到如下定理. 证明:当α=1时,命题1已证. 所以有 当n=1时,由于有g(z)∈B1,所以有 结论成立. 从而存在常数Nk+1,使得 下面给出一个具体的例子. 证明:简单计算可知f(z)是正规的,且g(z)∈B1.又因为 所以fu1(z)是正规的. 但是当f(z)和fu1(z)是都是正规的时,g(z)不一定属于B1.下面给出反例. 证明:因为有 所以f(z)是正规的. 所以有 故fu1(z)是正规的. 当z取实数并趋于1时有 所以g(z)∉B1. 反例2说明g(z)∈B1不是必要的. 由g(z)单叶解析,有 从而有 因此,fu1(z)是正规的.


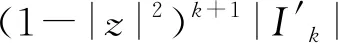

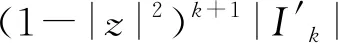


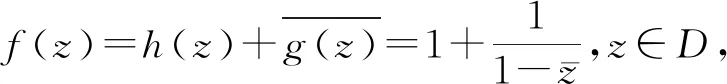





猜你喜欢
语数外学习·高中版上旬(2022年6期)2022-07-23
河北大学学报(自然科学版)(2020年2期)2020-05-23
人民调解(2019年2期)2019-03-15
卷宗(2018年14期)2018-06-29
读与写·教育教学版(2017年10期)2017-11-10
中学数学杂志(初中版)(2016年5期)2016-11-01
新高考·高一物理(2016年3期)2016-05-18
家庭用药(2016年7期)2016-05-14
中学数学杂志(初中版)(2015年6期)2016-01-07
数学教学(2013年3期)2013-05-15

