水泥土墙复合土钉墙的协同作用机理数值模拟
孙林娜, 徐福宾
(青岛理工大学 土木工程学院, 山东 青岛 266033)
基坑支护结构经过多年的实践和发展有多种形式,复合土钉墙作为其中的一类,是在土钉墙的基础上加入其他形式的辅助结构,形成以土钉墙受力为主的复合式基坑支护结构,目前,应用到实际工程中有7种形式[1].对于覆土性质、安全等级、降水要求、施工现场周围环境来说,复合土钉墙要比普通土钉墙优越许多,而且支护深度更深,深度已达21 m[2].水泥土墙复合土钉墙是7种形式之一,具有止水性能良好、基坑变形控制较强,以及经济效益较好等优点,可适用于含水率较高的软土场地.水泥土搅拌桩、截水帷幕、水泥土墙复合土钉墙是同一种支护结构,只是名称不一样.水泥土墙在土体开挖前施工完成,有超前支护的作用.搅拌桩不能很好地体现止水性能;截水帷幕仅可以体现止水性能;水泥土墙复合土钉墙可以同时体现支护作用和止水性能,较两者更为准确[3].不少学者通过现场试验[4]、模型试验[5],以及数值模拟[6-8]证实复合土钉墙各个结构之间确实存在着复杂的协同作用.但在实际工程设计中,常常采用简单叠加设计原理,进行两种及两种以上复合支护结构设计,对其中的协同作用机理研究不多.
协同效应最早在物理化学领域提出,指的是把两种及两种以上的成分或元素混合在一起所产生的作用效果,比各种成分或元素单独使用时的总作用效果要大,即“1+1≥2”的作用.1976年,哈肯[9]认为在整个系统中,发生作用的各个成分或元素之间都有着既相互合作又相互影响的关系.本文运用FLAC3D有限差分软件建立三维模型,对水泥土墙、土钉、土体3者在基坑动态开挖卸载过程中的协同作用机理进行数值模拟研究,使支护结构的参数选取更加合理.
1 模型的建立
1.1 工程实例
某城市广场基坑工程平面大致成方形,南北长95.50 m,东西长86.50 m,深 9.35 m.基坑周围环境较复杂,基坑东侧是20世纪90年代的低层住宅小区,西侧为某事业单位7层办公楼,北侧是已经建好的3层商业建筑,南侧为城市主干道解放东路.主要土层有杂填土、粉质黏土、黏土等,基坑支护结构方式为水泥土墙复合土钉墙,即设置两排深层搅拌桩形成水泥土墙(墙深为17 m,搅拌桩直径为 550 mm,墙厚为1 000 mm,两桩互相搭接为150 mm).土钉设置7排,每排倾角都为15.0°,土钉沿基坑深度布置形式为中部长上下短[1],中部3排等长均为13 m,上部两排和下部两排等长均为10 m.开挖一层支护一层,土钉水平间距均为1.30 m,最上部一排距开挖平面1.50 m,其余各排的竖直间距是1.30 m.在施工时,应及时将含有对中支架的螺纹钢筋放入钻孔直径为100 mm的孔洞中,钢筋直径为25 mm,分两次压力注浆后形成土钉.
1.2 三维模型的建立
基坑在开挖过程中具有明显的空间效应,如果不考虑空间协同作用,使用二维平面应变分析会使计算结果不安全或偏于保守,运用三维数值模拟分析是未来的趋势.基坑工程平面形状一般为不规则的形状,由于工程实例大致成方形,为了提升运算速度,在建立三维地质模型时,利用对称性选取1/4的开挖平面分析作用规律.地质模型和开挖部分的长×宽×高分别为100.00 m×50.00 m×30.00 m和30.00 m×20.00 m×9.35 m.模型边界条件如下:底面是固定支座边界约束竖直方向的变形;顶部开挖面取为自由面;前、后、左、右4面是可动滚轴支座约束侧向的变形.三维地质模型图,如图1所示.

图1 三维地质模型图Fig.1 3D geological model diagram
土钉用Cable结构单元进行模拟,力学参数如下:水泥浆体黏结强度为3.6×108Pa;水泥浆摩擦角为28.0°;弹性模量E为2.0×1011Pa;水泥浆体黏结刚度为8.0×105Pa.水泥土墙和土体选用摩尔库仑弹塑性模型,水泥土墙参数如下:泊松比μ为0.25;粘聚力c为2.0×105Pa;重度γ为21 kN·m-3;内摩擦角φ为35.0°,弹性模量E为6.0×1011Pa.根据地质勘察报告,影响土体开挖的现场土层自上而下分6层,由于2,3,4层为粉质黏土,参数相近划分为一层,5,6层为黏土,参数相近划分为一层.综合考虑各种影响,模型土层设计参数,如表1所示.表1中:h为土层厚度;K为体积模量;G为剪切模量.

表1 模型土层设计参数Tab.1 Design parameters of model soil layer
在大部分有限元模拟软件中,泊松比μ和弹性模量E使用较多,而在FLAC3D中,为了使计算结果更加准确,在赋值时输入的是体积模量K和剪切模量G,其导换公式为
G=E/[2(1+μ)],K=E/[3(1-2μ)].
2 基本作用规律的分析
2.1 水泥土墙水平位移
开挖完第一层土体时,水平位移表现为上部较大,下部较小并逐渐趋于零的“直角三角形”形状,其计算值如图2所示,实测值如图3所示.图2,3中:H为基坑深度;s为水平位移.

图2 水平位移计算值 图3 水平位移实测值Fig.2 Calculation values of horizontal displacement Fig.3 Measured values of horizontal displacement
随着土钉的植入和开挖深度的增加,形状不再是“三角形”,而是表现为“凸肚”的形状,主要是因为滑移面逐渐后移,土体影响范围增大,中部土体向坑内移动速度快,而上部土体移动较慢,导致位移曲线在中下部逐渐凸起,这也说明了复合土钉墙产生滑移破坏的现象与普通土钉墙是不同的.开挖完成后,中下部区域的水平位移比基坑其他区域大,开挖完成后水平位移云图,如图4所示.由图4可知:结果、实际监测数据和文献[10-11]位移变化规律相符.

图4 开挖完成后水平位移云图Fig.4 Horizontal displacement nephogram after excavation
计算值比实测值大主要是因为在实际监测时,测斜仪是从测斜管底部向上拉起,并设定测斜管底部为不动的点;而数值模拟时,监测点是沿水泥土墙外侧布设的,导致桩底水平位移计算值不为零.如果将图2的水平位移曲线减去底部所增加的位移,把桩底水平位移计算值归零,则结果是与实测是符合的.模拟计算的“凸肚”状比实测的要靠下,主要原因是模拟计算的土层参数、结构设计参数、模型网格空间受力等参数选取比较理想,影响因素较少,使得“凸肚”状有下移的趋势.
2.2 水泥土墙后的地表沉降
水泥土墙后的地表沉降范围和幅度随开挖深度的加深逐渐增大,模拟计算值,如图5所示;实测值,如图6所示;开挖完成后地表沉降位移云图,如图7所示.图5,6中:a为距离;b为沉降.

图5 地表沉降计算值 图6 地表沉降实测值Fig.5 Ground settlement calculation value Fig.6 Ground settlement measured value

图7 开挖完成后地表沉降位移云图Fig.7 Ground settlement displacement nephogram after excavation

(a) 第1排土钉轴力变化图
由图5,6可知:沉降幅度最大的地方不在基坑边缘,而是距基坑边缘约为1H~2H的地方,在土钉加固区域范围外,即在2H范围外,距离越远,沉降幅度越小,在1H范围内,距离越近,沉降幅度越小,1H~2H内沉降出现最大值,沉降完成后表现为“勺子”状,与文献[12]规律相似;模拟计算值的影响范围比实测值较远,沉降变化幅度也比较平缓,而实测沉降值逐渐趋于零,这主要是受施工场地大小的限制及周围已有建筑物的影响,同时也说明了计算模型的理想化和实际施工情况有一定的差别,但是基本变化趋势一致,能够反映地表沉降随基坑开挖的变化规律.
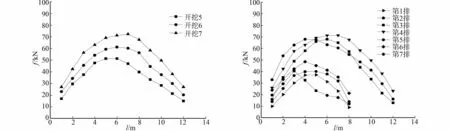
(b) 第4排土钉轴力变化图 (c) 开挖完成后各排土钉轴力变化图图8 土钉轴力变化图Fig.8 Axial force variation of soil nail diagram
2.3 土钉轴力
土钉轴力(f)沿其长度(l)的变化,如图8所示.由图8可知:土钉轴力表现为中、前部大,两头小的“枣核”形状,与文献[13-14]中土钉受力的特性一致.“枣核”形状说明土钉在土体介质中的摩阻力在潜在滑裂面处最大,同时,也说明土钉起到了使滑移面后移、传递荷载、限制水泥土墙变形、以及扩散土中应力的作用.由图8(c)中可知:开挖完成后各排土钉的最大轴力差别很大,上两排和下两排较小,中间3排较大,这与水平位移的“凸肚”状是相符的,其中第4排土钉的轴力最大,约是最顶排和最底排的两倍,沿其长度的“枣核”形状也比其他土钉丰满.
开挖完成后各排土钉轴力沿土钉长度变化云图,如图9所示.由图9(a)可知:靠近底部的土钉,轴力最大值有前移的趋势,而中上部轴力最大值有后移的趋势,说明滑裂面随基坑开挖有逐步向后移动的趋势,土体影响范围也逐渐扩大.由图9(b)可知:在基坑阴角处的土钉出现了微小的压力,主要是由于两边的水泥土墙互为支撑,在变形协调条件下,基坑中部土体向坑内移动明显,而在阴角处位移很小,相对中部来说有后移的趋势,这也说明基坑阴角处具有明显的空间效应,与文献[15]结果一致.

(a) 模型正视图 (b) 模型俯视图图9 开挖完成后各排土钉轴力沿土钉长度变化云图Fig.9 Axial force nephogram of each row soil nails along length after excavation
3 协同作用机理的分析
3.1 墙钉比

图10 墙钉比示意图Fig.10 Wall-nail ratio schematic diagram
在分析工程实例基本作用规律的基础上,通过改变水泥土墙宽、空间位置、土钉倾角3个参数,对水泥土墙、土钉、土体3者在基坑动态开挖卸载过程中的协同作用机理和破坏模式进行数值模拟研究.
根据以往的理论研究与工程实际经验,在稳定性分析中,最危险滑移面必然经过最长或最底部的土钉,土钉对复合土钉墙的稳定性贡献值一定大于零[1],因此,引入墙钉比(w)的概念.水泥土墙宽与土钉加固区域垂直投影方向长度的比值,简称墙钉比,墙钉比示意图,如图10所示.
由图10可知:水泥土墙通常形成防渗挡墙,作为止水帷幕;插入土体的深度由基坑周围地下水渗流作用控制,通常可满足稳定性的要求,所以选择改变水泥土墙宽进行协同作用机理研究;滑移面穿过土钉加固区域最下一排或最长一排土钉,如果把最长土钉垂直投影长度区域的土体看作加固区域,由于加固区域端部较小,使土钉总加固区域变小,所以取各排土钉的平均投影长度作为研究对象更为合理.土钉垂直投影长度是土钉长度的余弦值,所以知道土钉平均长度和倾角,就可以计算出土钉平均投影长度(Lv)及墙钉比(w),分别为
上式中:n为土钉排数;Ln为第n排的土钉长度;α为土钉倾角;D为水泥土墙宽度.
算例1土钉长度分别为10,10,13,13,13,10,10 m,平均长度为11.29 m,土钉倾角为15°,土钉平均投影长度为10.91 m,水泥土墙宽度为1.0 m,w=9.17%.
水泥土墙复合土钉墙的协同作用评价指标有很多,如土钉轴力、基坑底部隆起、地表沉降的幅度、整体稳定性安全系数、水泥土墙水平位移等.在这些指标中,最容易监测和观察的是水泥土墙水平位移,以水泥土墙水平位移为衡量目标,分析其与墙钉比的关系,探究墙钉比的取值范围.
3.2 水泥土墙宽的影响
对墙宽为0,0.5,0.8,1.0,1.2,1.5,2.0,2.5 m等8种情况分别建立模型,0 m指的是普通土钉墙.不同墙宽下的墙钉比计算值,如表2所示.表2中:Δmax为水平位移.由表2可知:普通土钉墙位移最大,

表2 不同墙宽下的墙钉比计算值Tab.2 Calculation values of wall nail ratio with different wall widths
在开挖到第5步时,稳定性已不满足要求;当水泥土墙从0 m增加到0.5 m时,位移明显减少,说明水泥土墙起到限制位移和增加稳定性的作用.
墙钉比为0%~7.00%时,限制位移明显,但是由于水泥土墙宽较窄抗剪强度较低,稳定安全系数不满足要求,上部土体容易发生倾覆破坏,如图11(a)所示;墙钉比为7.00%~12.00%时,位移减小明显,水泥土墙和土钉墙受力合理协同作用最好,二者相互作用以土钉墙受力为主;墙钉比为12.00%~20.00%时,增加墙钉比对减少水泥土墙最大位移的作用已不明显,随着墙钉比的增大,水泥土墙受力逐步增大,土钉墙受力逐步减少,达到一定程度时,形成以水泥土墙为主要受力体系的支护结构,不再是以土钉墙受力为主,已超出对复合土钉墙的概念范畴[1],受力机理有向重力式挡墙转化产生滑移破坏的现象,如图11(b)所示.

(a) 倾覆破坏 (b) 滑移破坏图11 不同墙宽下的破坏模式图Fig.11 Failure modes diagram under different wall widths
3.3 水泥土墙空间位置的影响
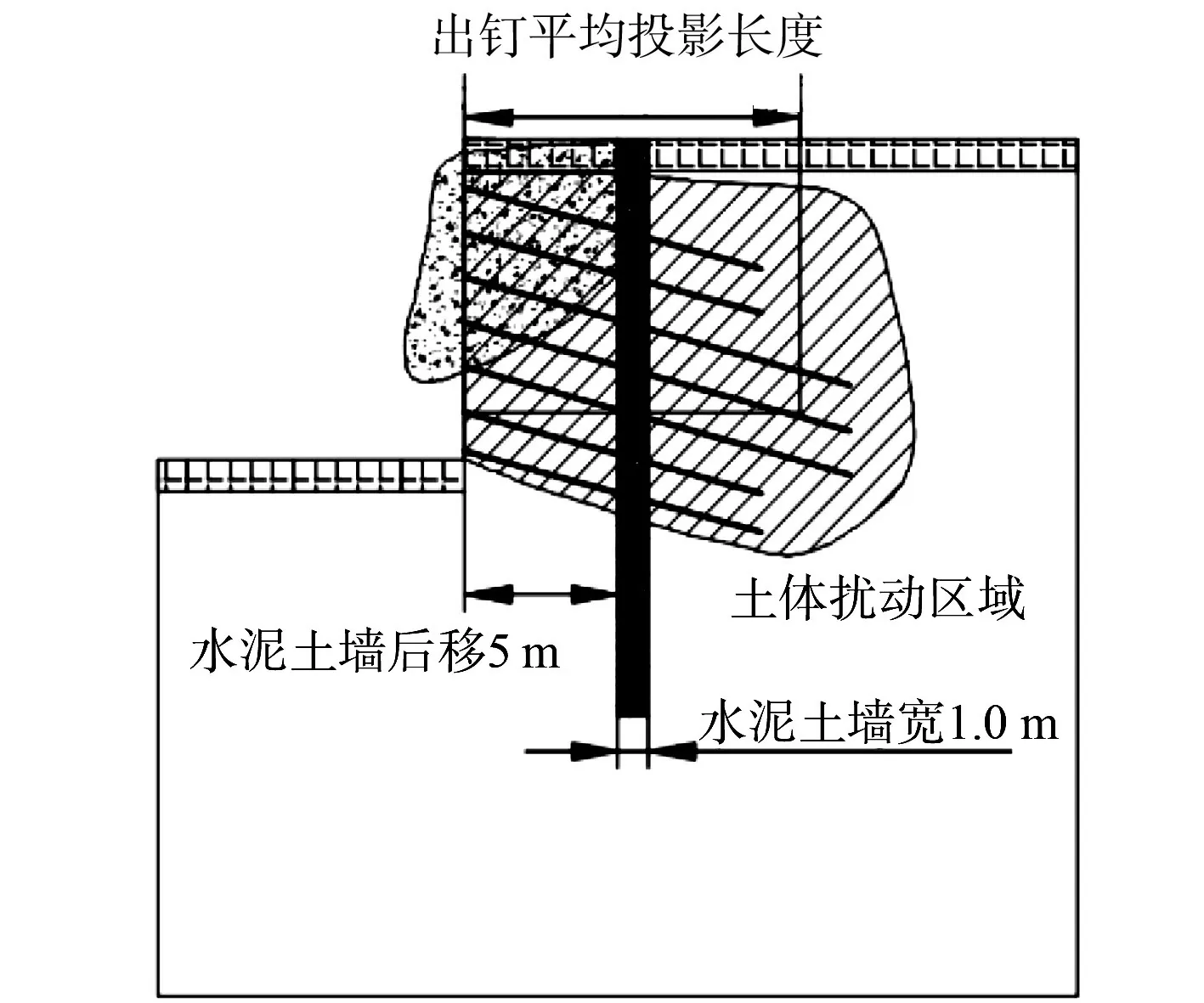
图12 局部滑移破坏图Fig.12 Local slip damage diagram
对水泥土墙距离基坑边缘分别为0,1,3,5 m,以及普通土钉墙的5种情况建立模型,土钉倾角为15.0°,墙宽为1.0 m,土钉平均投影长度为10.91 m.在墙钉比不变的情况下,普通土钉墙的水平位移最大,0 m时水平位移最小,说明水泥土墙在基坑边缘时,对水平位移约束效果最为明显.随着向后移动距离的增加,约束效果减弱,产生位移的主要是前部土体,产生局部滑移破坏的现象,如图12所示.
水泥土墙后移影响土钉轴力的发挥,因为土钉受力特性为前中部大、两头小的“枣核”形状,水泥土墙后移把土钉切成两段,前段土钉受力增加,后段土钉受力减少,使土钉沿其长度受力不合理.水泥土墙后移对土钉轴力发挥的影响,如图13所示.水泥土墙后移安全系数(ε)对比,如图14所示.
由图14可知:无水泥土墙时,安全系数最小;水泥土墙向后移动,对稳定性略有提高但作用不明显;在5 m时安全系数反而略有降低,主要是由于前部土体容易发生局部滑移破坏,与文献[16]中提到“水泥土墙前置稳定性更好”相符;在墙钉比不变的情况下,把水泥土墙放置在基坑边缘,约束水平位移明显,协同作用效果最好.

图13 水泥土墙后移对土钉轴力发挥的影响 图14 水泥土墙后移安全系数对比 Fig.13 Effect of backward movement of Fig.14 Comparison of safety factors for backwardcement soil wall on axial force of soil nails movement of cement soil wall
3.4 土钉倾角的影响
对土钉倾角分别为0°,5.0°,7.5°,10.0°,12.5°,15.0°,17.5°,20.0°,25.0°等9种情况建立模型,墙钉比计算值如表3所示,相对应的破坏模式如图15所示.
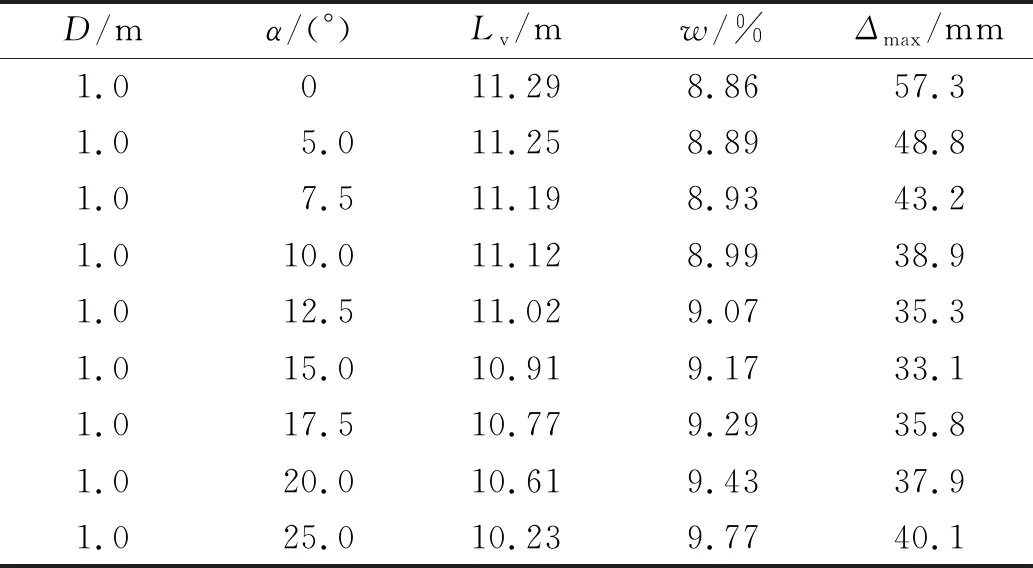
表3 不同土钉倾角的墙钉比计算值Tab.3 Calculation values of wall-nail ratio with different soil nail inclinations
由表3可知:倾角对墙钉比的影响范围较小,主要集中在8.80%~9.80%.当倾角为0°时,土钉水平排列,土钉加固区范围最大,但土体扰动范围也最大,在土体稳定区土钉的锚固段较小,扰动土体向坑内移动的范围逐渐增加,最终产生整体滑移破坏现象(图15(a)).

(a) 滑移破坏 (b) 倾覆破坏图15 不同土钉倾角的破坏模式图Fig.15 Failure modes diagram of different soil nail inclination angles
当墙钉比为8.90%~9.20%时,位移明显减少,在9.17%(倾角15.0°)处,最大水平位移最小,主要是由于滑移线缓慢前移,使土体扰动范围变小,水泥土墙受到土压力减少,而土钉锚固段增加,二者受力逐渐合理,协同作用明显;当墙钉比再次增加,水平位移逐渐增大,主要是由于随着土钉倾角增加,土钉加固范围变小,土钉加固盲区(图15(b)阴影部分)出现,加固盲区土体产生的重力传递给加固区域,进而作用在水泥土墙上,使水泥土墙上部受到的土压力逐渐增加,最终产生倾覆破坏的现象(图15(b)),土钉倾角过大会产生加固盲区[17],土钉倾角不宜超过20.0°[1]
文献[11]通过工程实例分析了复合土钉墙的位移、地质条件,以及支护设计参数之间的关系.墙钉比工程实例分析,如表4所示.表4中:土钉总长度(M).由表4可知:墙钉比在7.00%~10.00%之间的有8例,小于7.00%的有4例,大于10.00%的有4例,在7.00%~10.00%所占比例为50%.由于土钉倾角对墙钉比的影响范围较小,在8.90%~9.20%时,位移明显减少,最大水平位移较小,综合考虑各种因素的影响和工程实例分析,建议墙钉比取值范围为8.00%~9.50%(4例),此范围内支护结构受力合理,协同作用效果最好.

表4 墙钉比工程实例分析Tab.4 Analysis of wall nail ratio engineering
4 结论
为进一步明确复合式支护结构间的协同作用机理,在分析工程实例基本作用规律的基础上,引入协同作用的理念,提出了墙钉比的概念,将水泥土墙水平位移作为衡量指标,对水泥土墙复合土钉墙进行数值模拟分析,得到以下2个结论.
1) 水泥土墙水平位移曲线表现为“凸肚”状,开挖完成后最大值在中下部区域;地表沉降变化曲线表现为“勺子”形状,计算值的影响范围较远,变化幅度较平缓;土钉轴力沿其长度呈现出中、前部大,两头小的“枣核”形状,基坑顶部和底部的土钉轴力较小,中部较大.以上3种形状说明FLAC3D有限差分软件的数值模拟结果可以反映实际工程的变化规律.
2) 改变墙宽,当墙钉比在7.00%~12.00%时,水平位移最大值减少明显;在墙钉比不变的情况下,水泥土墙在基坑边缘时,约束水平位移最为明显,后移影响土钉轴力的发挥;改变土钉倾角,当墙钉比在8.90%~9.20%时,位移减少明显,最大水平位移较小.因此,在工程设计时,建议把水泥土墙放在基坑边缘,墙钉比取值范围控制在8.00%~9.50%,此范围内支护结构受力合理,协同作用效果最好.

