XMQ6838Y客车动力总成悬置系统参数的优化设计
盛精, 潘迎春, SOHAIL Aamir, 王志敏, 王蒙光
(1. 厦门理工学院 福建省客车先进设计与制造重点实验室, 福建 厦门 361024;2. 厦门理工学院 福建省客车及特种车辆研发协同创新中心, 福建 厦门 361024)
动力总成悬置系统是连接客车车架和动力总成之间的重要部件,它既能够降低动力总成传递到车架产生的振动,又能隔离客车在不同工况下传递给动力总成的振动.隔振性能的优劣是衡量客车品质的重要指标.在悬置系统隔振性能的设计研究方面,卢炽华等[1]选用悬置元件的静刚度作为设计参数,研究悬置系统模态解耦对隔振性能的影响;庄伟超等[2]讨论悬置元件的动刚度,解决了并联式柴电混合动力客车在怠速工况时方向盘的抖动问题;文献[3]探讨了悬置元件位置和动刚度参数对悬置系统隔振性能的影响.在悬置元件动刚度的优化方面,万里翔等[4]确立了以悬置系统支反力幅值最小作为目标;王国林等[5]尝试以支撑处加速度响应最小为目标;Luo等[6]选取悬置系统六自由度解耦率最大为目标,优化了悬置元件的位置和刚度.近些年来,部分学者以解耦率最大化为优化目标,在提升悬置系统隔振性能方面取得了一些的成果[7-9].在优化模型的求解算法方面,文献[10-13]分别采用NSGA-II算法蒙特卡洛算法、自适应模拟退火(ASA)等方法,优化了悬置系统参数.在上述的研究中,悬置系统相关的设计参数皆被视为连续型变量,然而,成本是客车企业考虑的重要因素,悬置元件仅有几种规格的刚度供选.因此,在悬置系统优化设计中,悬置元件位置连续化和刚度离散化问题成为关注的焦点.
鉴于此,本文针对XMQ6838Y客车动力总成悬置系统参数的设计(考虑怠速工况),选用解耦率为评价指标,探索在六阶模态下以悬置系统动刚度(离散型)和软垫安装位置(连续型)为设计变量的优化模型构建;同时,在MATLAB与iSIGHT集成环境下对各阶模态的解耦等相关技术开展相关研究.
1 悬置系统动力学模型的构建与评价
1.1 动力总成悬置系统力学模型的建立
悬置系统元件的布置形式、刚度和安装位置对悬置系统的隔振性能有不同程度的影响.各阶模态和固有频率是悬置系统的重要性能参数也是其固有属性,因此,获取悬置系统的固有频率和模态对其优化设计具有重要作用.相比乘用车,客车动力总成系统的质量大、体积大,且多采用四点式悬置.
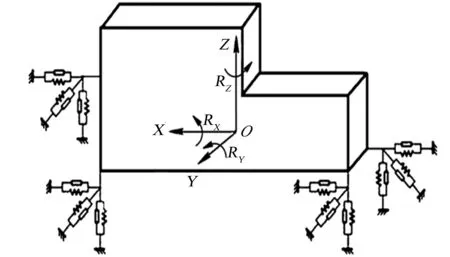
图1 动力总成悬置系统振动模型Fig.1 Vibration model of powertrain mounting system
根据动力总成和悬置系统的布置形式,建立四点式动力总成悬置系统振动模型,如图1所示,以求解悬置系统固有属性.图1中:以动力总成质心为原点建立坐标系;X轴正方向为纵向往发动机前端方向;Z轴正方向平行于气缸中心线,指向缸盖方向;Y轴依据右手定则确定;围绕X,Y,Z向旋转分别为RX,RY,RZ.
不考虑阻尼和外力作用,可得系统自由振动的微分方程,即动力总成悬置系统在广义坐标下的动力学方程为
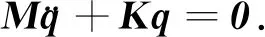
(1)
式(1)中:M为系统质量矩阵;K为系统刚度矩阵;q为系统位移向量.
利用拉斯变换可得
(ω2-A)q=0.
(2)
式(2)中:A=M-1K.
由式(2)可知:ω2是矩阵A的实特征值;矩阵A是非对称矩阵;q是ω2的实特征向量.因此,可获取悬置系统的六阶固有频率ωi和固有振型φi,i=1,2,…,6.

图2 搭载空调支架实图Fig.2 Equipped with air conditioning bracket real map
由于该型客车发动机与空调压缩机集成化程度低,两者分别进行单独布置.在开启空调时,皮带轮向空调压缩机进行功率输出,相当于动力总成引入外源激励,使该型客车悬置系统不能满足上述建立的悬置系统振动模型(无激励).陈述等[14]探究了空调压缩机悬置与动力总成悬置集成方案,但缺乏实证研究.因此,参考乘用车及国外客车压缩机与发动机的集成方案,采用将压缩机布置在发动机的前悬置上的结构形式,从而满足上述的悬置系统振动模型,同时适用于空调启、闭两种工况.搭载空调支架实图,如图2所示.
1.2 动力总成悬置系统的评价
相比能量解耦法,扭矩轴解耦法虽然能够提高侧倾模态方向上的解耦,但主要应用于前置后驱的动力总成布置形式,且需要构造特定的坐标系.能量解耦法能够摆脱动力总成的布置形式和类型的限制,可以在悬置系统自由振动方向上求解刚体模态参数,也可在初始坐标系上对悬置系统展开解耦设计,无需坐标转换;同时,其解耦率在0%~100%范围内,具有良好的数值计算稳定性[15].由于文中优化悬置元件刚度为离散而非同比例变化,能够消除能量解耦法的局限性,因此,采用能量解耦法实现评价悬置系统在六自由度方向上的解耦[16],解耦率表达式为

(3)
式(3)中:m(k,l)为系统质量矩阵M的第k行第l列元素;φ(k,j)为振型φ(j)的第k个元素;φ(l,j)为振型φ(j)的第l个元素.
通过获取动力总成质量和转动惯量得到质量矩阵M,利用悬置元件坐标和刚度求解系统刚度矩阵K.悬置软垫坐标参数,如表1所示.运用式(1)求解系统六阶固有频率fi和固有振型φi.将φi和质量矩阵元素m(k,l)代入式(3),求解该系统刚度下的解耦率Pi.悬置系统的固有频率(f)和解耦率(P),如表2所示.由表2可知:各向解耦率普遍低于80%,解耦程度低.部分固有频率间距小于0.5 Hz,固有频率分配不合理.
通过实车测试,得到怠速车内关键点振动的加速度,如表3所示.表3中:a表示加速度.由表3可知:开启空调时方向盘Y向振动加速度(3.43 m·s-2)与关闭空调时后排座椅的Z向振动加速度(0.94 m·s-2),均远不能满足方向盘(X,Y,Z三向振动加速度分别为0.4,0.4,0.2 m·s-2)和座椅(三向振动加速度皆为0.2 m·s-2)的乘坐舒适性标准,且其他方向也未能达到标准的下限.

表1 悬置软垫坐标参数Tab.1 Coordinate parameter of mounting cushion mm

表2 悬置系统的固有频率和解耦率Tab.2 Natural frequency and decoupling rate table of mounting system

表3 怠速车内关键点的振动加速度Tab.3 Vibration acceleration at key points in bus during idling m·s-2
2 悬置系统设计参数的优化设计
基于上述对各阶模态解耦率、固有频率和该车振动测试结果的分析,可以发现悬置元件的动刚度和安装位置仍有优化的空间.以解耦率为最大目标,综合考虑以空间布置、频率间距、元件刚度和关键模态方向的解耦率为约束条件,以位置和刚度为设计变量,开展对悬置系统参数的优化设计.
2.1 设计变量
悬置元件的安装角度的范围一般为30°~60°,而为防止剪切力过大,同时为获得较好的抗扭能力,前后悬置皆为45°.以悬置元件离散刚度和连续位置为设计参数,获取设计变量为
X=[x1,…,x4,x5,x6,x7,…,x14,x15,x16]T=[k1,…,k4,u1,v1,w1,…,u4,v4,w4]T.
(4)
式(4)中:k1~k4依次为前左、前右、后左、后右4悬置元件的刚度;ui,vi,wi分别为每组悬置元件在广义坐标系下的坐标值.
2.2 约束条件
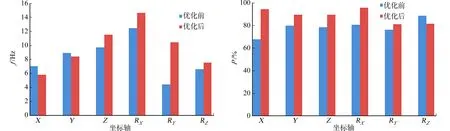
该车为四缸直列式柴油机且怠速为650 r·min-1,怠速频率为21.7 Hz,考虑隔振理论和路面向车体传递振动,悬置系统的固有频率为5 Hz 表4 悬置元件位置的约束范围Tab.4 Constraint range of mounting component position mm 优化设计动力总成悬置系统参数时,多以解耦率最大为目标.以刚体六自由度的解耦率最大为优化目标,实施对悬置系统的频率、位置、离散刚度和解耦率的约束.其目标函数和约束条件为 上式中:Pm(X)为第m阶振动解耦率;fm(X)为第m阶系统固有频率;ui(L),ui(U);vi(L),vi(U);wi(L),wi(U)分别为每组坐标值的上、下限. 图3 iSIGHT集成MATLAB优化图Fig.3 iSIGHT integrated MATLAB optimization map 通过集成iSIGHT和MATLAB,对悬置系统参数优化,优化流程,如图3所示.MATLAB提供程序脚本和运算,包括全部离散的动刚度数据库;iSIGHT提供对优化设计变量的选取和选型、约束条件的设定、目标和算法的确定.由于iSIGHT软件在调用遗传类优化算法时,只允许设定连续型的变量,对于文中离散的刚度无法胜任.考虑到自适应模拟退火方法能够对离散的变量进行优化,同时,此算法非常适合用短期运行分析代码解决高度非线性问题,并寻找全局最优解[1,17].在MATLAB脚本文件中,将全部离散的三向动刚度以向量的形式建立一个完整的动刚度数据矩阵,利用在脚本文件中编写匹配代码与iSIGHT中设置的离散变量建立一一对应的关系,防止优化后的离散动刚度与实际值匹配错乱. 利用iSIGHT选择相应离散化和连续化的设计变量,即刚度与位置.基于悬置系统,在空间尺寸上选取一定的步长,得到连续化的悬置元件位置参数;三向刚度设计变量离散化的处理过程则通过以下3个步骤. 步骤1建立所有悬置元件刚度的矩阵数据库.按照悬置元件不同的三向刚度值,建立独立的向量ks=(kus,kvs,kws)T,kus,kvs,kws为悬置元件三向主刚度,可供选择的前悬置元件刚度为k1,k2, …,ki,后悬置刚度为ki+1,ki+2,…,kn.为了使悬置刚度矩阵匹配得更加准确,将前、后刚度数据库分别使用不同字段并加以指定,则完整的刚度矩阵为K=[k1,k2,…,kn]T. 步骤2离散刚度数据矩阵.在优化过程中,由于前、后悬置采用不同字段加以区分,通过离散的数值s,识别并读取该刚度矩阵的列向量Ks.这样能够准确地搜索到前、后悬置对应的独立向量(kus,kvs,kws)T.按照列向量元素排布的原则,将向量的三元素匹配为悬置元件的三向动刚度值. 步骤3前、后三向动刚度值指代.利用优化的离散数值s定位悬置系统振动模型的前、后悬置变量,通过一一对应的方式将离散三向动刚度kus,kvs,kws指代到系统振动模型的刚度变量,即替代系统振动模型的离散刚度变量. 优化后的悬置系统的元件位置、动刚度、前悬置刚度保持不变,后悬置由初始[610,450,2 000]N·m-1优化为[390,290,1 500] N·m-1.优化后的悬置坐标,如表5所示. 表5 系统优化后的悬置坐标Tab.5 Optimized mounting coordinates mm 优化前、后的固有频率和解耦率对比,分别如图4,5所示.由图4可知:与优化前相比,优化后悬置系统固有频率的间距增加、分布更合理,且固有频率均在可控范围内,满足设计要求.由图5可知:悬置系统的解耦率除了在RZ向(81.6%)有所降低外,其他方向都有不同程度的提升,其中,Z向和RX向的解耦率由优化前的78.41%和80.85%分别提升至89.70%和95.89%,六自由度平均解耦率从78.65%提升至88.69%,达到了预期的效果. 图4 优化前、后的固有频率对比 图5 优化前、后的解耦率对比 Fig.4 Comparison of natural frequency Fig.5 Comparison of decoupling rate distribution before and after optimization before and after optimization 为了验证优化设计对实车悬置系统隔振性能的实施效果,对XMQ6829客车悬置系统进行改造,并利用LMS数据采集设备对优化后的关键位置进行测试工作. 实验使用LMS数据采集仪、上位机软件和三向加速度传感器.将三向加速度传感器分别布置在方向盘、前排座椅、中间排座椅和后排座椅,且选择合适的位置安装传感器.方向盘三向传感器和座椅三向传感器的安装位置,分别如图6,7所示.启动样车空挡并稳定在怠速,关闭空调时怠速为650 r·min-1,启动空调时怠速为800 r·min-1.采集频率范围为512 Hz,频率分辨率为1 Hz,对功率谱施加Hanning窗,信号记录时间不少于20 s,测试得到有效数据3~5组,处理数据是频率范围128 Hz.采用原地怠速时各测点的振动加速度均方根值进行评价,不区分启、闭空调的评测方法. 图6 方向盘三向传感器安装位置 图7 座椅三向传感器安装位置Fig.6 Installation position of steering Fig.7 Installation position of seat wheel three-way sensor three-way sensor 当怠速关闭、开启空调时,优化前、后客车内各关键点振动情况,如图8所示.由图8可知:当怠速关闭、开启空调时,优化后客车内各关键点的平均振动加速度由优化前的0.38 m·s-2和0.64 m·s-2,降低为0.21 m·s-2和0.29 m·s-2. 由图8(a)可知:当怠速关闭空调时,方向盘和后排座椅的三向振动加速度均大幅降低,振动加速度由0.94 m·s-2下降为0.23 m·s-2;从隔振效果看,前排座椅和中间排座椅最好,后排座椅较好,方向盘次之(略高于0.2 m·s-2),皆满足设计要求.由图8(b)可知:当怠速启动空调时,方向盘的Y向振动加速度降幅最大(由3.43 m·s-2下降为0.35 m·s-2);从隔振效果看,前排座椅、中间排座椅最好,方向盘、后排座椅次之.对比图8(a),(b)可知:在怠速状态下,启动空调时的隔振效果比关闭空调时要好. (a) 怠速关闭空调 (b) 怠速启动空调图8 怠速关闭、启动空调时优化前、后客车内各关键点振动情况Fig.8 Comparison of key point vibration acceleration in bus when air-conditioner shutdown and start-up at idle 通过对动力总成悬置系统参数展开优化设计,得到以下3点结论. 1) 运用以悬置元件离散刚度与连续位置为设计变量的优化模型,采用iSIGHT集成MATLAB的形式调用自适应退火算法,进行悬置系统参数的优化设计后,动力总成悬置系统垂直(Z向)和俯仰(RX向)模态解耦率分别由78.41%和 80.85%提高至89.70%和95.89%,系统的各阶模态解耦率均得到了大幅提升. 2) 系统优化后,怠速关闭空调时,后排座椅的振动加速度由0.94 m·s-2下降为0.23 m·s-2,隔振效果明显;怠速开启空调时,方向盘的Y向振动加速度由3.43 m·s-2下降为0.35 m·s-2,消除了方向盘抖动过大的问题. 3) 优化后悬置系统的六自由度平均解耦率从78.65%提升至88.69%,改善了系统的各阶模态解耦程度;通过实车测试怠速开启、关闭空调的两种运行状态,可知车内关键点的平均振动加速度由0.38 m·s-2和0.64 m·s-2降低为0.21 m·s-2和0.29 m·s-2,解决了该车怠速振动剧烈的问题.
2.3 优化目标和算法

2.4 设计变量的处理
2.5 优化结果与讨论

3 实证分析


4 结论

