异型石材高效锯切优化策略

钱平， 邵辉， 尹方辰， 兰欣， 王达

(1. 华侨大学 信息科学与工程学院， 福建 厦门 361021；2. 华侨大学 福建省电机控制与系统优化调度工程技术研究中心， 福建 厦门 361021；3. 华侨大学 制造工程研究院， 福建 厦门 361021)

石材行业的发展对石材加工提出更高的要求，尤其是在粗加工阶段，加工效率倍受关注.传统的石材粗加工多采用金刚石砂轮磨削或线锯锯切的方式[1-2]，然而，这些加工方式的时间消耗往往不能很好地满足粗加工高效率的需求.金刚石圆锯片因切割深度深、切割线速度大，被广泛应用于石材的切断工艺[3].随着多轴联动技术的发展与5～6轴数控机床的应用，三维锯切加工逐渐成为研究热点.近年来，国内外学者开始采用圆锯片代替传统刀具，用于粗加工工序的研究.吴玉厚等[4]提出一种基于刀触点路径截面线法，利用圆锯片对小曲率的曲面进行粗加工，相比砂轮磨削，其加工效率提高了5倍.针对数控加工过程中实时仿真的工件建模方法，现有的方法多采用基于留量的Z-map模型反映工件的残留情况[5]，但大量的数据计算会占用较大的存储空间.张霞等[6]提出一种基于B-rep的工件表面动态几何模型，但对模型适用性没有作出进一步的分析.传统数控粗加工一般采用等参数线偏置法[7]和截面线层切法[8]进行材料去除规划，以生成刀具轨迹.然而，这些方法存在刀路冗长或计算获取不易等局限性.

已有文献对金刚石圆锯片在异型石材大块锯切粗加工中应用的研究较少，本文结合石材粗加工阶段的特点与金刚石圆锯片优势，以材料去除量和锯切加工时间为评价指标，提出基于圆锯片的异型石材粗加工优化策略.

1 关键问题

粗加工是数控加工的重要工序之一，其任务是快速切除工件毛坯上的大部分多余材料，只保留后续工序的适当余量[9].金刚石圆锯片粗加工三维异型石材，具有实现高效化、自动化的大块锯切粗加工能力，其大块锯切示意图,如图1所示.

图1 大块锯切示意图Fig.1 Schematic diagram of block sawing using circular sawblade

研究解决的关键问题描述有以下3点.

1) 对锯切粗加工而言，应着重于刀具与工件模型的几何求交快速性和工件数据操作高效性.因此，需建立一种适用于锯切过程中工件数据的高效动态管理的工件模型及数据结构.

2) 锯切粗加工应尽量保证每次锯切的材料去除量大，因此，需要在三维异型石材表面搜索材料去除深度最大时对应的特征切削点，进而构建确定圆锯片姿态的锯切平面.

3) 在进给速度一定时，锯切加工时间主要由锯切进给行程确定，为实现最短锯切加工时间，必须确定最短锯切的进给行程.

实际加工过程中，需要综合考虑加工效率和加工余量.为实现材料去除规划与进给方向优化策略，作出以下3个假设:1) 基于材料去除最大深度的锯切平面搜索是在毛坯工件选定为合理加工余量的前提下展开的；2) 算法产生的锯切平面姿态均在机床的机构约束范围之内；3) 仅对工件在粗加工过程中的单工序、不换刀情况进行进给方向优化.

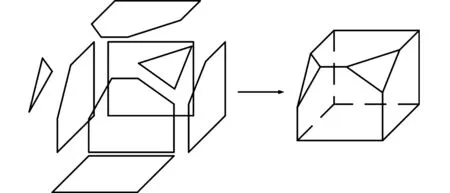
图2 工件模型的边界表示法Fig.2 Boundary representation of workpiece model

2 工件建模

材料去除过程中，工件的几何形状与数据随锯切的进行而动态变化，这是一个大计算量和大信息存储的复杂过程[10].圆锯片大块锯切石材的过程，不需要工件表面形貌的精确表示，而需要简单且能详细描述构成物体表面几何特征的描述方法.工件模型的边界表示法，如图2所示.边界表示法具有几何元素的信息及相互间的拓扑关系描述能力[11]，可以方便地提取和动态存储物体的各个组成面、面的边界及各个顶点的数据信息.因此，工件的动态描述过程可用边界表示法.物体的实体(SH)可通过它的空间平面方程及一定拓扑关系的边界面顶点表示，其表达式为

SH=(PH，EH，FH).

(1)

式(1)中:PH，EH和FH分别表示实体相应的顶点集、边集和边界面集，PH包含顶点的坐标信息，EH包含构成边的邻接顶点信息，FH包含构成边界面的顶点及其法向量信息.

工件模型数据结构,如图3所示.图3中:Id solidno，Id faceno，Id Edge，Id Vertex分别为体表、面表、边表，顶点表中各实体、面、边及顶点的编号；Face_prevs，Face_nexts为与面相邻编号的两个面，体表、边表，顶点表规则与之类似；Face_vector为面的法向量；Edge_vtx1为边的约束顶点；Vertex_coordinate为顶点的空间坐标.

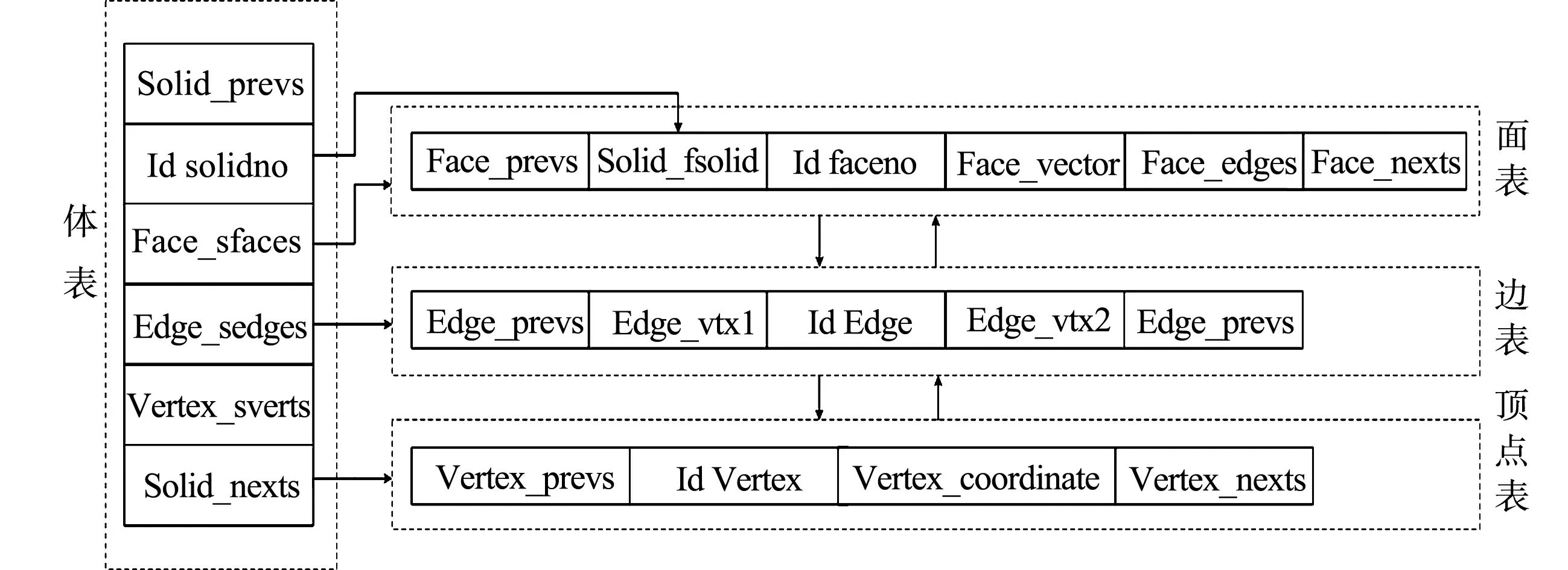
图3 工件模型数据结构Fig.3 Data structure of workpiece model

实体(solid)由体表构成，表达封闭表面围成的有限空间;边界面(face)由面表构成，表达实体表面，带有方向性;边(edge)由边表构成，表达相邻边界面的相交边，每条边由两个邻接顶点约束;顶点(vertex)由顶点表构成，体现边的约束顶点.

3 材料去除规划

不同于传统粗加工方法，锯片可实现大块锯切，依据此特点进行材料去除规划.对于凸体形状的工件材料，由空间几何推理可知，锯切材料去除量正相关于材料去除最大深度[12].基于此，提出一种基于材料去除最大深度的锯切平面算法.

图4 高去除量锯切示意图Fig.4 Schematic diagram of high removal sawing

3.1 算法流程

高去除量锯切示意图，如图4所示.材料去除最大深度的锯切平面算法流程，如图5所示.图4,5中：Dm,max为材料去除最大深度；Pbc，Pobjc分别为材料去除最大深度对应的特征工件顶点与特征切削点；Pbp，out1，Pbp，out2为锯切去除工件顶点；Pb1～Pb8为工件顶点；Lh1,Lh2,Lh4,Lh5为锯切相关邻边;Lh3为锯切无关邻边；πc为高去除量锯切平面;Pb，new1～Pb，new4为圆锯片沿πc锯切工件后，在工件表面产生的截交面顶点.

图5 材料去除最大深度的锯切平面算法流程Fig.5 Flow chart of sawing plane algorithm of material removal maximum depth

3.2 三角网格模型的八叉树划分

八叉树是一种通过生成立方体空间节点包络空间点集，并递归形成树状层次结构的三维体素化方法[13].为提高特征切削点搜索效率，首先，基于异型石材的三角网格模型表面数据点集(x，y，z)的分布范围，根据合理加工余量的假设条件，构建一个紧致包围盒将点集数据完全包含，得到八叉树第0层的根节点；然后，根据设定的八叉树深度，沿着3个坐标轴方向，对该节点进行递归划分.八叉树划分空间区域示意图，如图6所示.

以常见异型石材制品路障球为例，其直径为400 mm，实际加工时，通常将毛坯工件设置与加工目标尺寸相近，尺寸(长×宽×高)为440 mm×440 mm×400 mm，保证一定的加工余量.以减少切割工序为准，对于异型石材，取均匀加工余量为最佳.当八叉树层数较多时，八叉树储存空间占用和节点查询时间消耗的代价会随之增加[14].综合考虑搜索效率与节点查询时间消耗等因素，以8个近邻子空间建立深度为2层的八叉树，将路障球三角网格实体模型表面数据划分为8组，分别纳入子空间节点区域Areali(i=1，2，…，8)，从而在异型石材轮廓表面数据点与八叉树的节点之间建立联系.路障球的八叉树区域划分,如图7所示.

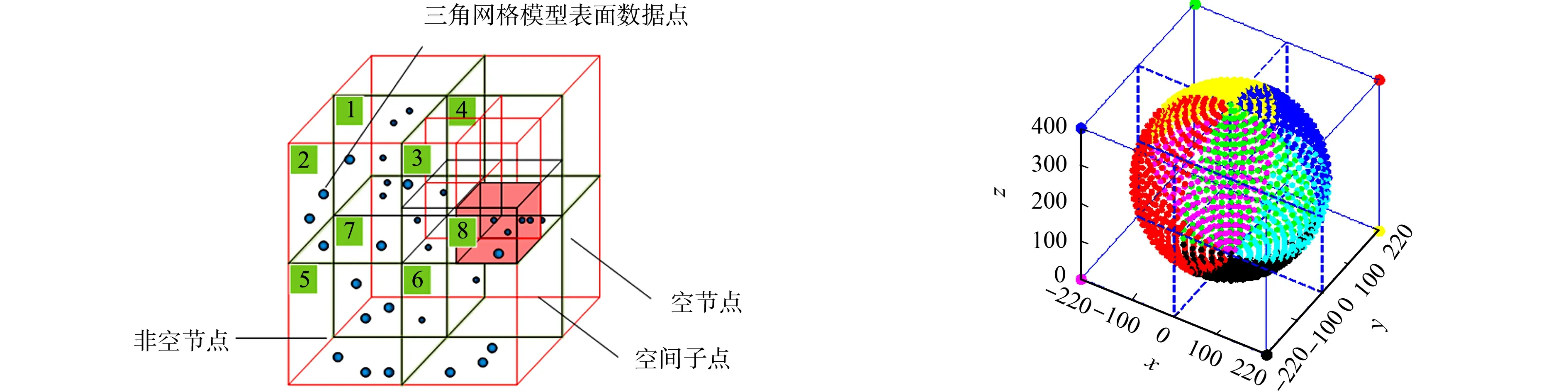
图6 八叉树划分空间区域示意图 图7 路障球的八叉树区域划分Fig.6 Schematic diagram of space area division with octree Fig.7 Roadblock ball division with octree

3.3 高去除量锯切平面构造

设定毛坯工件尺寸与异型石材的三角网格模型包围盒一致.在此基础上，根据工件顶点与八叉树划分的空间节点区域的位置关系，判断工件顶点所属空间节点区域Areali，并在该空间节点区域中搜索工件顶点到异型石材轮廓表面的距离Dm.将Dm的极大值Dm，max作为材料去除最大深度，逆向搜索得到相应的特征切削点Pobjc(xobjc，yobjc，zobjc)与特征工件顶点Pbc(xbc，ybc，zbc).

以特征切削点与特征工件顶点构造πc的法向量K(KA，KB，KC),即

K(KA，KB，KC)=(xbc-xobjc，ybc-yobjc，ybc-yobjc).

(2)

由于特征切削点属于πc的切点，通过解析几何求解，可以得到πc的平面方程为

KA·x+KB·y+KC·z+KD=0.

(3)

式(2)，(3)中:KA，KB，KC，KD为锯切平面的系数.

锯切平面算法用于连续锯切规划，通过算法得到有序的锯切平面πc，圆锯片沿πc进行锯切加工可以保证高材料去除量指标.高去除量锯切平面，如图8所示.

(a) 算法搜索的第1次锯切平面 (b) 顺序搜索的第2次锯切平面图8 高去除量锯切平面Fig.8 High removal sawing planes

3.4 锯切材料去除量计算

为观测圆锯片每次锯切去除材料的效果，需要对锯切材料去除量Vc进行计算，有以下3个步骤.

步骤1判断锯切去除工件顶点.πc将全空间分割成两个半空间[15]，通过其法向量定义正、负半空间.以πc为边界，其法向量所指向的一个半空间为正半空间，即锯切去除部分所在的半空间，负半空间为工件材料保留部分.利用工件顶点和πc的平面方程，根据二叉空间分割算法，判断锯切去除顶点,即

(4)

步骤2求解锯切截交面顶点.分析πc与工件的相交位置关系，提出锯切平面与锯切相关邻边求交算法.将锯切相关邻边的空间直线方程与πc平面方程构建方程组,即

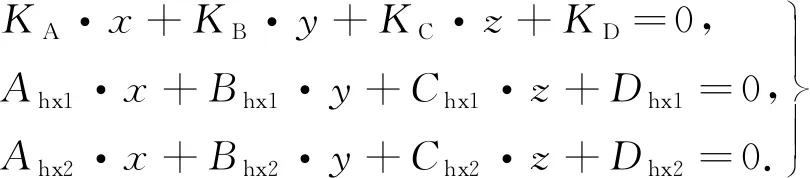
(5)

式(5)中:Ahx1，Bhx1，Chx1，Dhx1，Ahx2，Bhx2，Chx2，Dhx2分别是锯切相关邻边的空间直线方程系数.求解方程组，得到锯切截交面顶点Pb，new={Pb，new1，Pb，new2，…，Pb，newn}.

步骤3计算锯切材料去除量.根据工件去除体与锯切截交面的关系可知，Pbp，out={Pbp，out1，Pbp，out2，…，Pbp，outn}与Pb，new={Pb，new1，Pb，new2，…，Pb，newn}构成工件去除体的所有顶点.考虑材料去除过程中工件去除体与工件完全分离，因而,可以将工件去除体视为规则的凸多面体.根据三维空间多面体体积公式[16]，可计算工件去除体体积，进而得到锯切材料去除量Vc,即

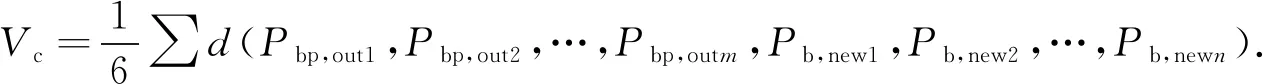
(6)

式(6)中:d(Pbp，out1，Pbp，out2，…，Pbp，outm，Pb，new1，Pb，new2，…，Pb，newn)为工件去除体表面多边形顶点按逆时针排列时，顶点坐标所构成的正向行列式.

4 锯切加工时间优化

4.1 锯切加工时间优化模型

考虑一次锯切走刀切透的方式[17](简称一刀切透方式),沿前文规划的锯切平面πc加工.在忽略非锯切运动消耗时间的前提下，锯切加工时间优化模型为

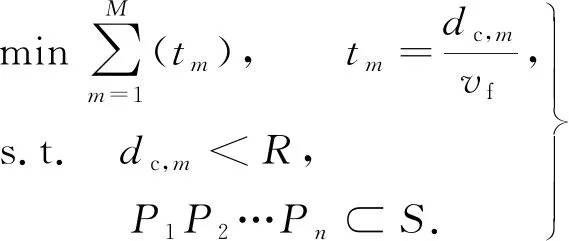
(7)

式(7)中:M为锯切次数;tm为沿锯切平面加工所消耗的时间;dc，m为沿锯切平面加工的锯切进给行程(一刀切透方式下的锯切深度);vf为锯切进给速度;R为圆锯片半径;P1P2…Pn为锯切截交面多边形;S为一刀切透方式下的锯切弧区[18].

M由材料去除规划获取的πc数量决定，实际加工中,vf通常取定值.为了最小化锯切加工时间，应保证每次锯切加工所消耗的时间tm最小，而tm与vf,dc，m直接相关.

4.2 优化方法

由时间优化模型可知，锯切进给行程是影响锯切加工时间的主要因素，其与进给方向及下刀点选取有关.不同进给方向的锯切进给行程，如图9所示.由图9可知：刀轴始终保持垂直于锯切截交面多边形P1P2P3，选取不同的进给方向和下刀点均能实现一刀切透，但锯切进给行程存在差异；相比进给方向1，进给方向2的锯切进给行程更长，在相同的进给速度条件下，进给方向2的锯切加工时间也会相应增加.因此，欲获得最小的锯切加工时间，需要对锯切截交面多边形进行分析，寻找使锯切进给行程最短的进给方向和下刀点.

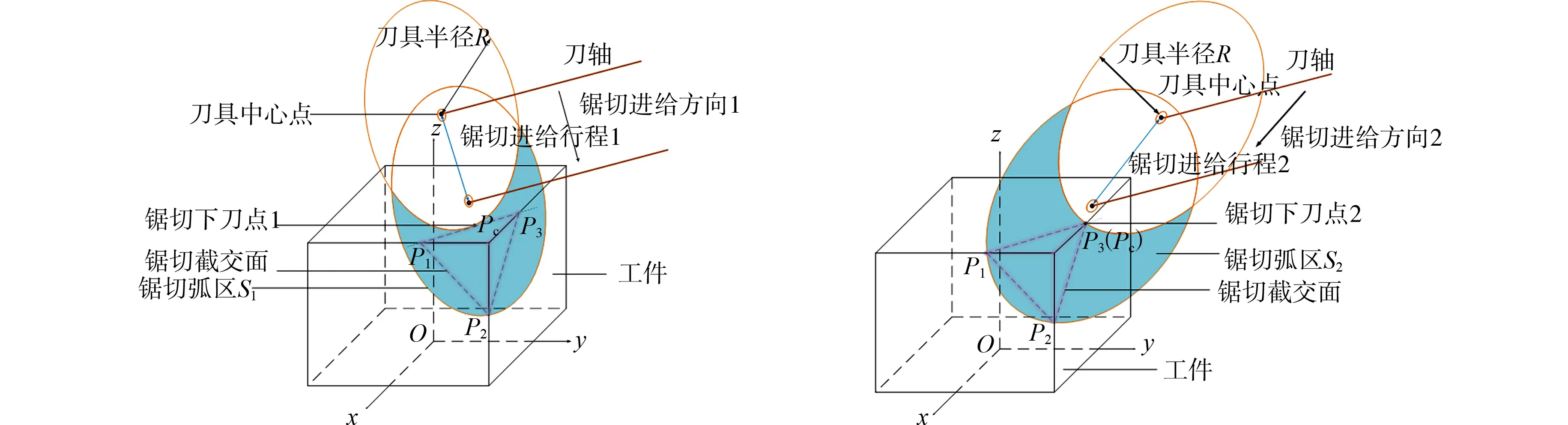
(a) 进给方向1 (b) 进给方向2图9 不同进给方向的锯切进给行程Fig.9 Sawing feeding strokes for different cutting directions

4.2.1 锯切截交面多边形分析 为了方便锯切截交面多边形分析，给出如下4个定义.

定义1设P1P2…Pn是锯切截交面的三维空间凸多边形，其顶点按逆时针排序.

定义2设Li，i+1={Pi，Pi+1}为P1P2…Pn的一条边，顶点Pj(j=1，2，…，n)到边Li，i+1的距离为Di，j，则称hi，j=max(Di，j)(j=1，2，…，n)为边Li，j的高，其对应的顶点称为高顶点Ph.

定义3设hi，j为多边形P1P2…Pn的一条边的高，则称hmin=min(hi，j)为多边形的最短高，最短高的长度称为多边形P1P2…Pn最小跨度.

定义4多边形P1P2…Pn最小跨度hmin对应的边为锯切特征边Lp.

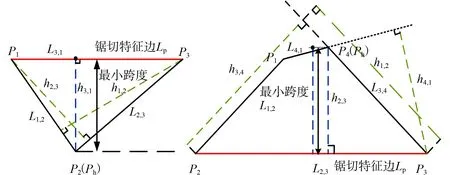
图10 锯切截交面多边形的最小跨度Fig.10 Smallest span of intersecting polygon

以锯切截交面多边形P1P2P3与P1P2P3P4为例.锯切截交面多边形的最小跨度,如图10所示.图10中:P1P2P3中最短高为h3，1,高顶点Ph为P2,锯切特征边Lp为L3，1,最小跨度为h3，1的长度；P1P2P3P4中最短高为h2，3，高顶点Ph为P4，锯切特征边Lp为L2，3，最小跨度为h2，3的长度.

分析锯切截交面多边形特性可知，最小跨度一定存在于多边形的某一条边的高hi，j中.

4.2.2 进给方向优化方法 选取锯切截交面多边形最小跨度的进给方向和满足多轴机床几何特性的下刀点，进而可以确定最短锯切进给行程，具体优化方法如下.

首先，对锯切截交面多边形P1P2…Pn进行分析，在其边集合L={L1，2，L2，3，…，Ln，1}中依次取边Li，i+1，根据Li，i+1={Pi，Pi+1},求出边的空间直线方程为

(8)

然后，依次取锯切截交面多边形顶点Pj(j=1，2，…，n)，根据点到空间直线的距离公式,求解所有顶点Pj到边Li，i+1的距离Di，j(j=1，2，…，n)，并得到边Li，i+1的高hi，j.进而，确定锯切截交面多边形的最短高、最小跨度、锯切特征边Lp及其对应的高顶点Ph.

最后，分析锯切特征边与其对应高顶点的位置关系，以确定进给方向和锯切下刀点.若锯切特征边Lp对应的高顶点Ph位于Lp的下方，则选取该Ph在Lp上的垂足点为锯切下刀点，以其对应的最短高hmin方向为最优进给方向，最短锯切进给行程为锯切截交面多边形的最小跨度；若锯切特征边Lp对应的高顶点Ph位于Lp的上方，则选取该Ph为锯切下刀点，以其对应的最短高hmin方向为最优进给方向，为实现一刀切透方式，最短锯切进给行程为锯切截交面多边形的最小跨度加上一定的锯切补偿深度.

5 仿真实例与对比分析

5.1 仿真结果分析

考虑一定的粗加工余量，选定尺寸(长×宽×高)为440 mm×440 mm×400 mm的长方体毛坯工件，取粗加工精度为Dst=26 mm，圆锯片半径为400 mm，锯切进给速度设定为180 mm·min-1，经过19次锯切后，材料去除规划获取的19个锯切平面，如图11(a)所示.边界表示法对粗加工锯切后的工件重建效果图，如图11(b)所示.可见锯切后的工件轮廓已逐渐逼近路障球形状.

锯切加工时间的对比，如图12所示.由图12可知：优化后的总锯切加工时间约为25 min，相较于未优化的锯切加工时间减少了约9.5%.

锯切加工过程中,单位时间锯切材料去除量(Vt)的对比，如图13所示.由图13可知：锯切材料去除量达到1.091×107mm3，约占应去除毛坯材料总量的81.2%.

(a) 锯切过程中的锯切截交面 (b) 锯切后的工件重建效果图 图11 仿真实验结果Fig.11 Simulation experiment results

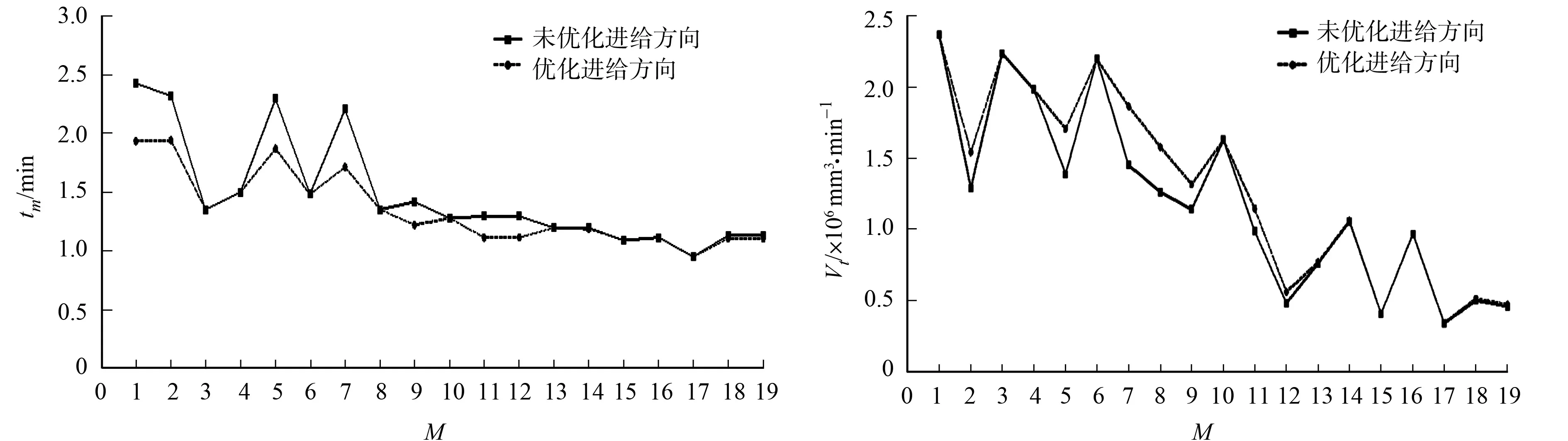
图12 锯切加工时间的对比 图13 单位时间锯切材料去除量的对比 Fig.12 Comparison of sawing time Fig.13 Comparison of removal amount of sawing material per unit time

5.2 锯切和磨削加工对比分析

为了验证锯切粗加工方法对提高异型石材制品加工效率的有效性，选择石材粗加工常用的磨削加工方式作为对比.砂轮加工参数如下：加工深度ap为2 mm；加工宽度aw为22.5 mm；进给速率为5 000 mm·min-1.圆锯片的锯切加工参数如下：圆锯片半径为400 mm；锯切进给速率为180 mm·min-1.在相同材料去除量1.091×107mm3的情况下，磨削加工时间为177 min，锯切加工时间为25 min.

对比两种加工方式消耗的时间可知：在相同材料去除量的前提下，锯切粗加工效率约为磨削粗加工的7倍.主要原因是磨削加工受到磨削深度的限制，其最大磨削深度仅能达到2 mm，且对于加工深度较深的情况必须采用分层磨削的方法；而文中的锯切加工方法能直接达到最大深度进行大块锯切，因此，加工效率显著提高.

6 结束语

采用边界表示法建立适用于锯切粗加工的工件模型及以边界面与顶点为核心的数据结构，实现了材料去除过程中工件表面数据的高效动态管理.提出基于材料去除最大深度的锯切平面算法用于锯切粗加工规划.在忽略非锯切运动的基础上，建立锯切加工时间优化模型.通过分析进给方向和锯切下刀点对锯切进给行程的影响，结合一刀切透方式，给出一种进给方向优化方法，实现了锯切加工时间最小化目标.在相同材料去除量条件下，通过锯、磨削加工时间对比，验证了文中锯切粗加工策略的高效性.