基坑钢支撑轴力监测的优化及实践

楼 岱，池玉宇，张国良，喻成刚，尹铁锋，陈俊峰

(1.宏润建设集团股份有限公司宁波分公司，宁波 315100；2.宁波市建设工程安全质量管理服务总站，宁波 315040)

随着我国城市化进程的加快，地铁建设热潮已席卷全国。但地铁建设的工程事故也屡见不鲜，仅2003～2010年间，国内地铁建设共发生118起地铁施工事故，且基坑事故占大多数[1]。实际基坑工程事故都有预兆，特别是软土地基基坑，都有一个从量变到质变的过程，做好施工过程中的监测工作，可有效避免工程事故的发生[2-5]。

支撑体系和围护墙共同承担了基坑的侧向水土压力，当实际支撑轴力与设计计算轴力不一致时，将可能引起围护体系失稳，因此支撑轴力监测是基坑监测中至关重要的一环[6]，支撑轴力监测方面的研究也越发受到重视。贾坚等[7]研发了钢支撑轴力伺服系统，并应用于紧邻地铁区间隧道的“大上海会德丰广场”深大基坑工程中，有效确保了基坑围护结构变形及地铁隧道变形控制在设定目标内。张德标等[8]运用钢支撑轴力应力伺服系统，减少钢支撑轴力损失，并对基坑临近地铁侧向变形最大点进行监测，确保了周边居民建筑的安全和地铁运行安全。黄卫华[9]采用无线自组网式钢支撑应力监测系统，在钢支撑轴力监测重点部位布设应力传感器进行实时监测，确保了地铁车站深基坑施工开挖过程中钢支撑施工安全和工程质量。程宏才等[10]针对当前基坑监测和预警中的信息化程度不高的现状，提出了一种对支撑轴力的智能化数据采集、数据预测和数据预警的系统设计方法。赵瑞传[11]、武进广[12]和马荣[13]等均结合实际工程，采用振弦式反力计监测基坑重要断面的钢支撑轴力的变化，分析了钢支撑轴力在基坑施工过程中的变化规律。

本文针对基坑钢支撑轴力监测中因偏心受压导致数据“失真”现象，采用增加轴力计钢弦数量，取平均值的方法进行优化，分别从理论分析、数值模拟和工程实践三方面阐述论证了优化方法的可行性。提高了基坑支撑轴力监测的准确性和可靠性，对同类工程具有一定的参考价值。

1 钢支撑轴力监测中的偏心受压

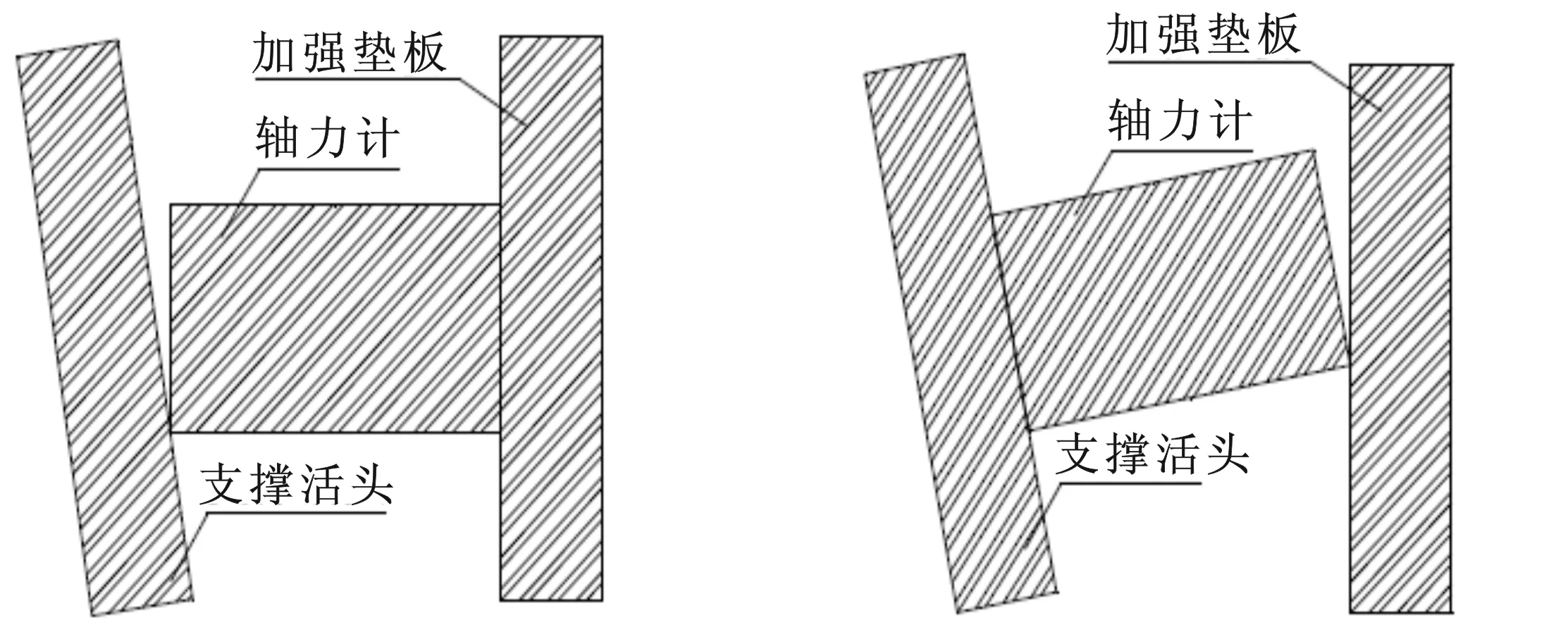
1-a 支撑活头与轴力计局部脱空 1-b 加强垫板与轴力计局部脱空

实际工程中安装钢支撑轴力计时由于接触表面不平整、安装误差以及局部变形等诸多原因，极易导致钢垫板(或支撑活头)与轴力计接触面局部脱空，使轴力计处于一定的偏心受压状态(图1)。由于所施加力值并未直接反映到轴力计钢弦上，使得传统的单弦轴力计难以克服偏心受压带来的测量误差，在小量程范围内影响更为明显。

因此，基坑钢支撑轴力监测的优化可考虑对传统单弦轴力计进行改进，以减小钢支撑安装过程中轴力计可能存在的偏压导致支撑轴力测量不准的影响。改进思路为增加轴力计钢弦数量(3根)，采用取平均值的方法来减小偏心受压的影响。

2 钢支撑轴力监测优化

2.1 理论分析

图2 振弦式轴力计内部结构示意图

振弦式轴力计内部结构如图2所示，主要由振弦丝、夹线器和感应线圈等组成。轴力计承压底面与振弦丝相连，振弦丝上被预加一定张力固定于传感器内。

根据经典弦原理，钢弦在弦长及受力一定情况下，其固有频率是固定不变的。当弦长一定时，钢弦固有频率的平方只与弦的张力成正比关系。当钢支撑受力作用于轴力计承压面上使其发生微小变形时，会导致与承压底面相连接的钢弦长度发生变化，即张力发生变化，其固有频率亦随之改变。钢弦固有频率的平方与承压面上所受压力成反比关系，通过监测钢弦频率的变化，即可得到被测钢支撑的轴力大小。

由振弦式轴力计工作原理，可得出三弦轴力计的钢支撑轴力计算公式为

(1)

(2)

式中：P为当前时刻相对初始时刻的累计轴力变化量，kN；Pn为当前时刻第n根弦相对初始时刻的累计轴力变化量，kN，n=1, 2, 3；Kn为第n根弦标定系数，kN/Hz2；fni为第n根弦当前时刻的输出频率，Hz；fno为第n根弦初始时刻的输出频率，Hz；KT为振弦式轴力计温度修正系数，kN/℃；Ti为振弦式轴力计当前时刻的温度值，℃；T0为振弦式轴力计初始时刻的温度值，℃。

由式(1)、式(2)可知道，三弦轴力计通过测量每根弦的频率，取平均值后得出钢支撑的轴力，从而减小因偏压引起的测量误差。

2.2 数值模拟

为验证增加钢弦数量，取平均值的方法可减小偏心受压的影响，利用有限元软件建立了量程为0～300 T的三弦/单弦轴力计偏心受压数值模型，模型为直径140 mm、高122 mm的圆柱体，模型底部为固支边界。然后对比分析了1/3、1/2和2/3面积偏压加载三种工况下轴力计的相对误差(图3)。

为研究相同偏压情况下，钢弦位置即三弦轴力计放置角度对监测结果的影响，采用了图4所示的钢弦取点方式，由图4可知，用中心点来模拟单弦轴力计钢弦位置，用外围等边三角形3个顶点来模拟三弦轴力计3根弦的位置。图中取点方式a为有一根弦位于受压区最底部，取点方式b为在a的基础上沿顺时针旋转30°，取点方式c为在b的基础上沿顺时针旋转30°。

3-a 1/3面积偏压 3-b 1/2面积偏压 3-c 2/3面积偏压 4-a 方式a 4-b 方式b 4-c 方式c

图3 三种计算工况

Fig.3 Three calculation conditions

图4 钢弦取点方式

Fig.4 Different arrangements of steel wire

表1 模拟计算结果

注：外荷载均为-38 977 kPa。

数值模拟结果如表1所示，取三弦平均值(或单弦值)与外荷载的相对误差作图，如图5所示。由图可知，三种计算工况下，布置方式a、b的三弦轴力计相对误差均小于单弦轴力计；2/3面积偏压工况下，布置方式c的三弦轴力计相对误差也小于单弦轴力计，但1/3面积偏压和1/2面积偏压工况下结果相反。

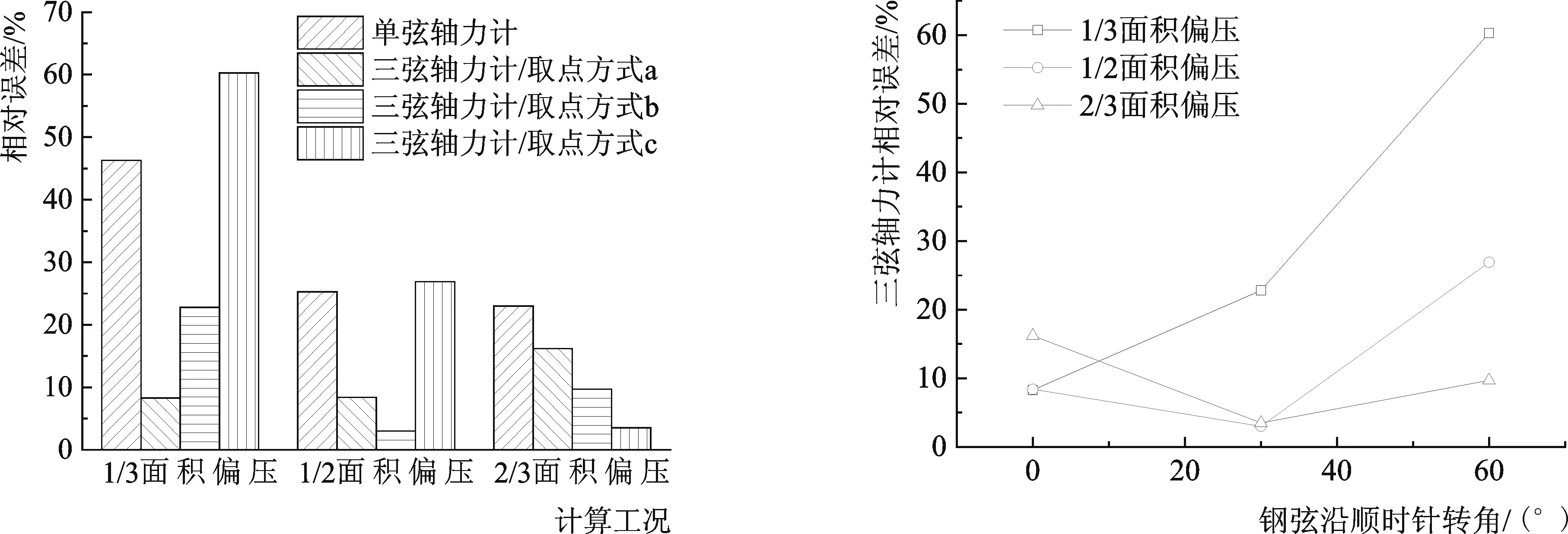
图5 三弦/单弦轴力计相对误差对比图

Fig.5 Comparison of relative error between three-string axial force meter and single-string axial force meter

图6 三弦轴力计相对误差随轴力计放置角度的变化

Fig.6 The relative error of three-string axial force meter change with the arrangement of steel wire

图6所示为三种计算工况下三弦轴力计相对误差随轴力计放置角度的变化曲线，横坐标为钢弦沿顺时针的转角(取布置方式a的转角为0°)，纵坐标为三弦轴力计的相对误差。由图可知，对于大偏心(1/3面积偏压工况)，转角在0°附近时三弦轴力计相对误差最小；对于小偏心(1/2面积偏压和2/3面积偏压工况)，效果较好的转角在10°～40°之间，此时三弦轴力计相对误差可控制在10%以内，转角为30°时，相对误差可控制在3%以内。

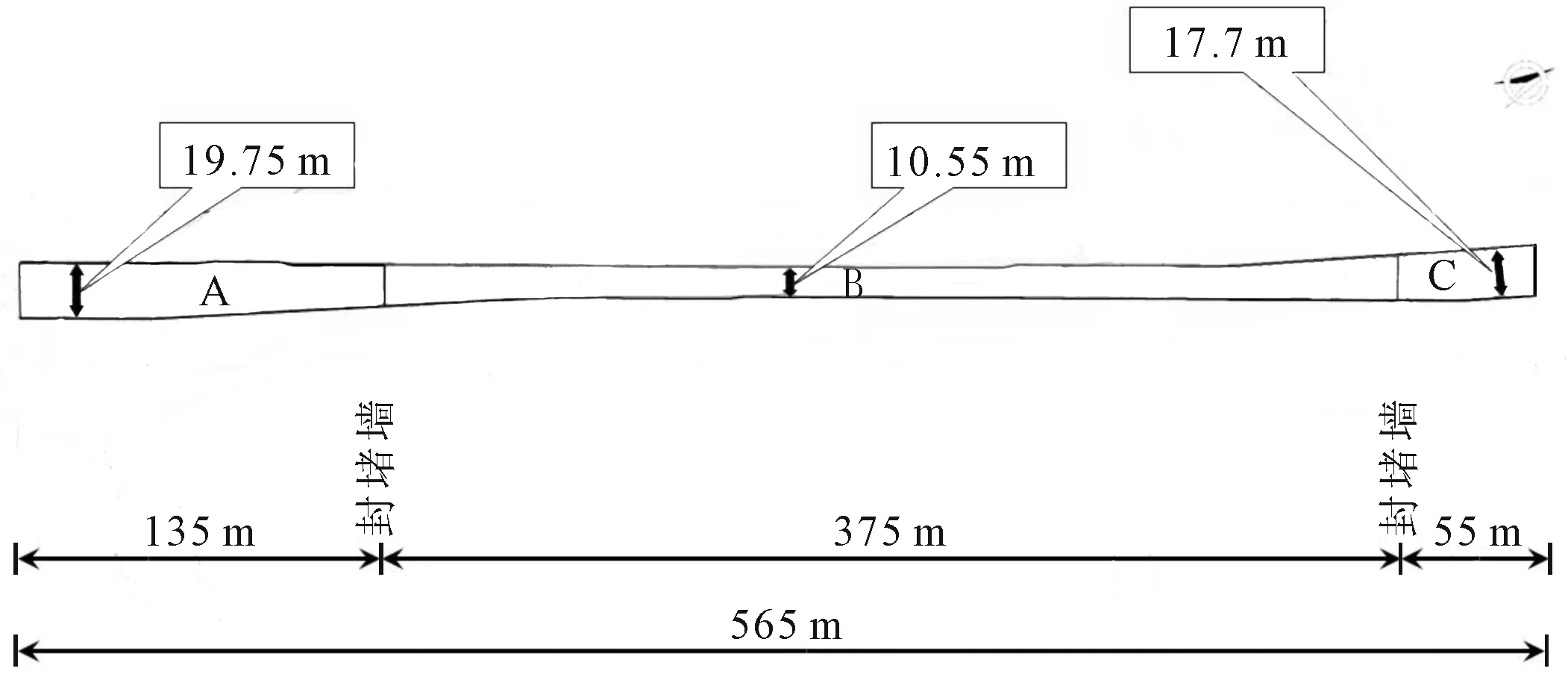
图7 基坑平面图

数值模拟的结果表明：当三弦轴力计的放置角度合理时，偏心受压造成钢支撑监测数据“失真”的现象可得到很好的改善，也验证了通过增加轴力计钢弦数量(3根)取平均值的方法来减小偏心受压影响的钢支撑轴力监测优化思路可行。

3 工程实践

以宁波地区某基坑工程为依托，开展钢支撑轴力监测优化的实践。

3.1 工程概况

基坑长565 m，宽10.55～19.75 m，开挖深度13.9～16.4 m。该基坑由封堵墙分为3个小基坑，从左到右依次编号为A、B和C(如图7所示)。基坑场地工程地质情况从上自下依次为：①1a杂填土，平均层厚1.6 m；①2黏土，平均层厚1.4 m；①3b淤泥质黏土，平均层厚2.0 m；②1黏土，平均层厚0.7 m；②2b淤泥质黏土，平均层厚14.7 m；③2层粉质黏土夹粉砂，平均层厚1.8 m。根据现场情况选择A基坑进行钢支撑轴力监测验证。A基坑围护结果为800 mm地下连续墙，支撑自上而下分别为1道混凝土支撑+4道钢支撑。基坑开挖时，第1～4层土体开挖至相应钢支撑底面以下0.3 m，故第1～5层土体开挖深度依次为3.9 m、3.3 m、3.3 m、3.3 m、2.4 m。

3.2 测点布设

钢支撑轴力监测点的布置如图8所示。由图可知，5个断面、4道钢支撑共布置了20个三弦轴力计监测点。

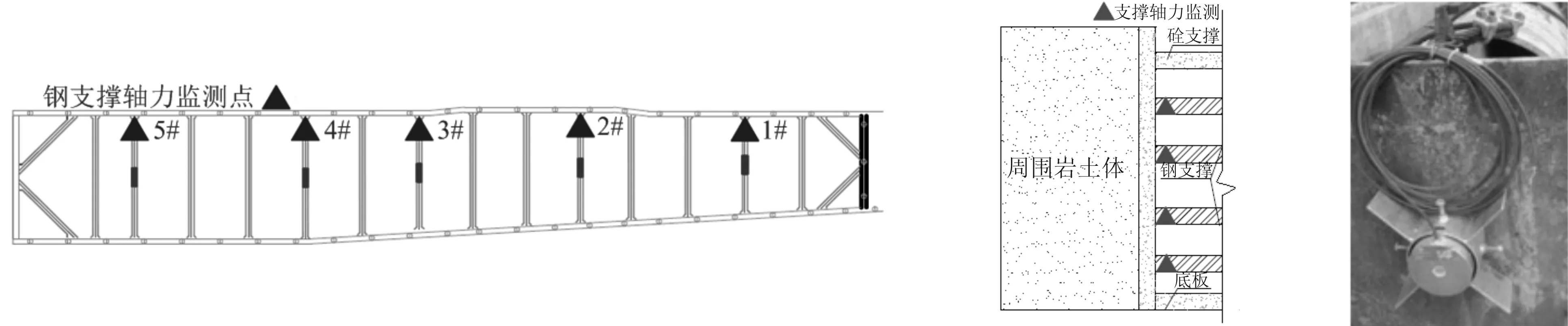
8-a 平面图 8-b 立面图 8-c 三弦轴力计

图8 测点布置示意图及三弦轴力计

Fig.8 Sketch of the layout of measuring points and three-string axial force meter

3.3 结果讨论

(1)钢支撑轴力预压值验证。

图9所示为1#断面上3道支撑预加压力后的轴力监测图，由图可知，3道支撑预加压力后的轴力实测值依次为755 kN、836 kN、595 kN，与设计预压值750 kN、900 kN、600 kN较为吻合。

9-a 1#断面第1道钢支撑 9-b 1#断面第2道钢支撑 9-c 1#断面第3道钢支撑

图9 钢支撑预加压力后的轴力实测

Fig.9 The measured force after steel support preloading

(2)轴力实测值与现场工况的匹配。

10-a 1#断面第1道钢支撑 10-b 2#断面第1道钢支撑

图10 1#、2#断面第1道钢支撑实测轴力时程曲线

Fig.10 The change curve of measured force of first steel support of 1# section and 2# section

图10所示为1#、2#断面第1道钢支撑实测轴力随时间变化曲线。图10-a、图10-b的变化规律基本一致，以图10-a为例进行分析可知，第1层土开挖完后，ZL1-1上限值为设计预压轴力750 kN；第2层土开挖，轴力增大至1 250 kN；第3层土开挖，轴力增大至最大值1 450 kN；第4层土开挖，轴力逐步减小至1 200 kN；第5层土开挖，轴力持续减小至1 000 kN。

图11所示为第2、3层土体开挖4#断面第1道钢支撑实测轴力随时间变化曲线。由图可知，ZL4-1正下方土体开挖时轴力增大速率最大，第2层土开挖完后，ZL4-1轴力稳定在700 kN，增大了约200 kN；第3层土开挖完后，ZL4-1轴力稳定在800 kN，增加了约100 kN。

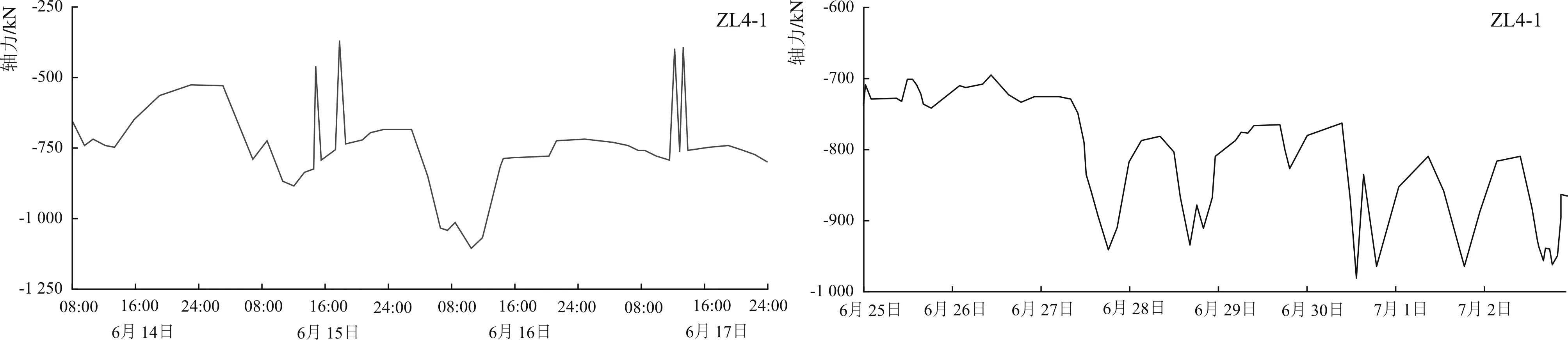
11-a 第2层土体开挖4#断面第1道钢支撑实测轴力 11-b 第3层土体开挖4#断面第1道钢支撑实测轴力

图11 第2、3层土体开挖4#断面第1道钢支撑实测轴力时程曲线

Fig.11 The measured force of first steel support of 4# section with the second and third layer of soil excavating

综上所述，实测的钢支撑轴力时程曲线呈现在当前工况支撑下挖土，支撑轴力增大；后续工况架设的支撑下挖土，先行工况的支撑轴力发生适当调整，后续工况支撑轴力增长的规律。符合基坑支撑轴力的基本变化规律，也说明了通过增加钢弦数量，取平均值的方法来优化基坑钢支撑轴力的监测可行。

4 结论

本文采用增加轴力计钢弦数量，取平均值的方法对基坑钢支撑轴力监测进行优化；首先理论分析了三弦轴力计的轴力计算公式，其次模拟对比了不同偏心受压状态下三弦、单弦轴力计的相对误差，最后进行工程实践。所得主要结论如下：

(1)三弦轴力计通过测量各弦频率，取均值后得出钢支撑的轴力。三种计算工况下，布置方式a、b的三弦轴力计相对误差均小于单弦轴力计；只有在2/3面积偏压工况下，布置方式c的三弦轴力计相对误差小于单弦轴力计。

(2)对于大偏心(1/3面积偏压工况)，转角在0°附近时三弦轴力计相对误差最小；对于小偏心(1/2面积偏压和2/3面积偏压工况)，转角在30°附近时，三弦轴力计相对误差最小。

(3)钢支撑实测轴力时程曲线呈现在当前工况支撑下挖土，支撑轴力增大；后续工况架设的支撑下挖土，先行工况的支撑轴力发生适当调整，后续工况支撑轴力增长的规律。

(4)钢支撑实测轴力符合基坑支撑轴力的基本变化规律，也说明了通过增加钢弦数量，取平均值的方法来优化基坑钢支撑轴力的监测可行。