调和γ-正规映射和调和γ-正规型映射

乔金静，翟小雨

(河北大学 数学与信息科学学院，河北 保定 071002)

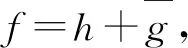
即在D上，|h′(z)|>|g′(z)|或|ω(z)|<1，这里ω(z)=g′(z)/h′(z)是f的伸缩[1].

记H(D)为D上的调和映射类，记A(D)为D上的解析函数类.设解析函数f∈A(D)，常数γ∈(0,∞)，如果

则称f为γ-正规函数[2].特别地，γ=1时，称f为正规函数[3].

正规函数对于亚纯函数性质的研究，特别是亚纯函数的边界性质的研究，是非常重要的.相关的结果，参见文献[3-4].文献[5]定义并研究了调和正规映射，从而把正规函数推广到调和映射的情形.本文给出调和γ-正规映射的概念，并研究其性质.

那么称它为调和γ-正规映射.

及其上的半范数‖f‖N(γ)∶=|f(0)|+βγ(f).

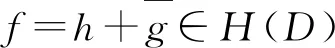
那么称它为调和γ-正规型映射.

作为经典的Bloch空间的推广，Colonna研究了调和Bloch空间[6].近年来,调和Bloch空间被推广到调和γ-Bloch空间[7].在文献[8]中，作者定义了调和γ-Bloch型空间，将调和γ-Bloch空间的一些结果推广到了调和γ-Bloch型空间上.显然调和Bloch映射是调和正规映射，但反之不成立.本文的主要目的是研究调和γ-正规映射和调和γ-正规型映射的性质，主要讨论调和γ-正规映射和调和γ-正规型映射的如下性质：仿射不变性、线性不变性、包含关系、与局部一致单叶调和映射的关系及从属原则.从而推广文献[8]中调和γ-Bloch空间和调和γ-Bloch型空间的相应结果.

1 仿射不变性、线性不变性及包含关系

(1)

若||a|2-|b|2|>1，由式 ⑴ 得

若||a|2-|b|2|<1，由式 ⑴ 可得

因此,A∘f∈NH(γ).

因此

(2)

若||a|2-|b|2|>1，由式 ⑵ 得

若||a|2-|b|2|<1，由式 ⑵得

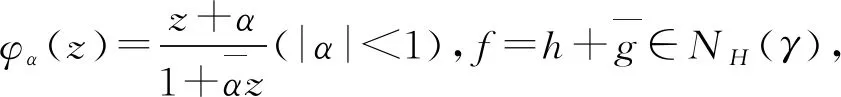
故f∘φα∈NH(γ).

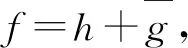
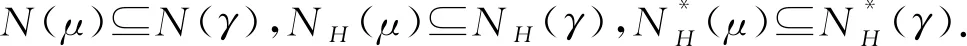
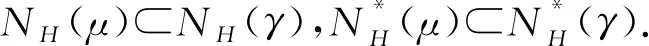
故fγ∈N(γ).但是当x∈(0,1)且x→1-，0<μ<γ时，

故fγ∉N(μ).结论得证.

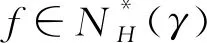
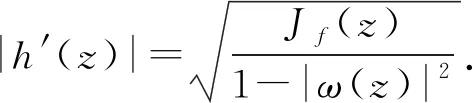
因为|g′(z)|<|h′(z)|，z∈D，而

因此

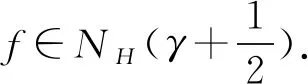
2 调和γ-正规映射、调和γ-正规型映射和局部一致单叶调和映射的关系

局部一致单叶调和映射f也可以用pre-Schwarz导数及其范数来刻画.f的pre-Schwarz导数及其范数分别定义如下[10-11]：

与文献[11]中定理7的证明类似，函数f是局部一致单叶的当且仅当‖Pf‖<∞(也可参考文献[12]).定义调和映射类

PH(γ)={f∶f是D上保向的调和映射，且‖Pf‖≤γ}

证明：对于γ>0，假设f∈PH(γ).因为fz(0)≠0，考虑函数

显然F在D上是保向的，满足规范化条件F(0)=Fz(0)-1=0，且有‖PF‖=‖Pf‖.因此，F∈PH(γ).由文献[12]得

因此

考虑函数

3 从属原则

2000年，Schaubroeck将解析函数从属的概念推广到调和映射的情形[13].设f和F是D上的2个调和映射，如果存在解析函数φ满足φ(0)=0和|φ(z)|<1，使得f=F∘φ，那么称f从属于F，记为fF.如果存在D上的解析函数φ满足|φ(z)|<1，使得f=F∘φ，则记为f≼F.明显地，若fF，那么f≼F.

证明：这里仅需要证明调和γ-正规型映射的情况，调和γ-正规映射情形的证明类似.

Jf(z)=JF(φ(z))|φ′(z)|2，

由Schwarz-Pick引理，(1-|z|2)|φ′(z)|≤1-|φ(z)|2.因此