交流伺服系统的高响应电流环控制
赵云, 廖政斌, 王泽飞, 蔡美东
(湖北工业大学 太阳能高效利用及储能运行控制湖北省重点实验室, 湖北 武汉 430070)
通过控制永磁同步电机(PMSM),交流伺服系统可实现高效率、高精度、高响应性能的目标[1-2].常用的控制方式有比例-积分(PI)控制和滞环控制.PI控制虽然简单、方便,但交轴(q轴)与直轴(d轴)存在耦合,影响电流环动态响应[3];滞环控制的电流环响应虽快,但该算法下的开关频率不固定,输出的电流含有谐波畸变,且存在稳态误差[4-5].因此,为了提高伺服系统电流环响应性能,保证电流稳定输出,可通过速度指令前馈和加速度指令前馈提高系统响应,并通过三次谐波的注入降低调制波的幅值,提高直流电流的利用率.文献[6-7]在一个载波周期内对定子电流进行双采样和双脉冲宽度调制(PWM)刷新,以减少采样延时,提高系统的响应性能.然而,以上方法在提高电流环带宽方面都较为单一.基于此,本文针对不同的延时采取不同解决方法,提出一种复矢量解耦的电流环预测控制算法.
1 交流伺服系统电流环PI控制性能分析
1.1 电流环模型



图1 电流环PI控制算法的结构框图Fig.1 Structural block diagram of current loop PI control algorithm
在同步旋转坐标系下,可得q轴电压Uq为
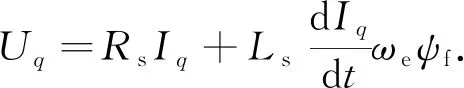
(1)
式(1)中:Iq为q轴电流;ψf为永磁体磁链.
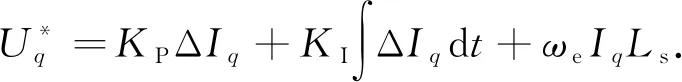
(2)
式(2)中:ΔIq为q轴电流的变化量.

(3)
式(3)中:Tc为一个控制周期.


图2 电流采样时序示意图Fig.2 Schematic diagram of current sampling sequence
由式(4)可知:电流环带宽和控制周期成反比.一个控制周期Tc存在采样延时、控制算法计算延时和PWM输出延时等情况,从而影响电流环响应性能.电流采样时序示意图[8],如图2所示.图2中:p为脉冲个数;a~g为采样时刻;k为周期个数;Tsw为逆变器开关周期.
1.2 电流环延时分析
在PI控制算法的电流采样中,Tc=Tsw.占空比在脉冲数递减为0时刻进行更新;在a时刻,系统对电流进行采样,得到采样电流,通过电流环预测控制算法计算逆变器输出占空比,再执行其他控制任务;在c时刻,系统将占空比更新到PWM发生器的比较单元,并在该开关周期内保持不变;在e时刻,逆变器产生输出电压.由此可知,典型电流采样时序的电流环延时Td=2Tc.
为改善输出电压滞后的问题,采用占空比双次刷新电流采样,占空比在脉冲数递增到峰值时刻和递减到0时刻进行更新,电流环的控制周期缩减一半,即Tc=0.5Tsw,电流环延时变为Td=Tc,但控制周期的减小会加重运算负荷,因此,对控制器运算性能要求较高.
占空比双次刷新PI控制算法虽然可解决电压输出滞后的问题,但电流采样仍存在延时.在占空比双次刷新电流环预测控制算法中,在a时刻进行电流采样,通过数字信号处理器(DSP)的模数转换进行坐标变换,并与给定电流进行比较;再通过电流环预测控制算法进行控制,从而产生下一个控制周期起点(b时刻)的控制电压[9];最后,进行占空比的计算和PWM的更新.该过程虽然通过电流预测下一个控制周期的电压抵消了电流采样延时,但仍存在一个控制周期的延时[10],即Td=0.5Tc.
2 复矢量解耦的电流环预测算法
本时刻采样的电流通过预测控制算法可得到下一时刻的预测电压,并作为电流环的输出[11],从而抵消采样延时,减少控制延时,提高电流环响应性能.通过对d-q轴电压进行复矢量解耦[12-13],可进一步提高电流环响应性能.
2.1 电流环预测控制
电流环预测控制算法的数学模型有如下4点假设:1) 忽略电机的铁心饱和;2) 不计电机的涡流损耗和磁滞损耗;3) 转子上没有阻尼绕组,永磁体也无阻尼作用;4) 电机的感应反电动势为正弦波.
永磁同步电机在旋转坐标系下的电压方程[10]为

(5)
式(5)中:Ud为永磁同步电机的d轴电压;Id为d轴电流;ψd,ψq分别为d轴磁链和q轴磁链;Ld,Lq分别为d轴电感和q轴电感.
在表贴式同步电机中,有Ld=Lq=Ls,由电压方程可推出电流的状态方程[10]为

(6)
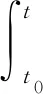
(7)
式(7)中:t0为初始时间;τ为时间变化值.
u在t0~t恒不变,设t0=kTs,t=(k+1)Ts[10],Ts为采样时间,可得
x(k+1)=Aφx(k)+A-1(Aφ-E)Bu(k)+A-1(Aφ-E)D(k).
(8)

(9)
根据电流环预测控制原理,I(k+1)=I*(k+1),故第k个周期的控制变量U(k)为

(10)
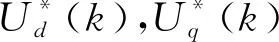


图3 电流环预测控制算法的结构框图Fig.3 Structural block diagram of current loop predictive control algorithm
2.2 复矢量解耦控制


图4 复矢量解耦的电流环预测控制算法的结构框图Fig.4 Structural block diagram of current loop predictive control algorithm of complex vector decoupling
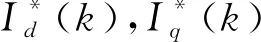
3 仿真实验分析
在Matlab/Simulink软件中,采用PI控制算法和电流环预测控制算法进行仿真.电机参数:电机额定电流为6 A;额定转速为2 000 r·min-1;额定转矩为5 N·m;定子电阻为3.15 Ω;定子磁链为0.175 Wb;定子电感为0.008 5 H;电机极对数为4;转动惯量为0.008 kg·m2.
直流母线电压为310 V,电流采样频率为20 kHz,载波频率为10 kHz.在0时刻,速度给定为1 000 r·min-1的阶跃指令,并在0.10 s时,突加5 N·m的恒定负载.三相电流和d-q轴电流波形均可反映交流伺服系统瞬态和稳态的运行情况.
PI控制算法和电流环预测控制算法下的三相电流和d-q轴电流,如图5所示.图5中:I为电流.由图5(a)可知:PI控制算法的电流含有大量的谐波,这是由于该算法存在严重的滞后问题,波形中含有大量的噪声导致波形成非正弦.由图5(b)可知:电流环预测控制算法的三相电流波形基本为正弦波.由图5(c),(d)可知:当0.10 s突加负载时,图5(d)的d轴电流比图5(c)的波动更小;在稳态情况下,无论电机空载或带载,相较于PI控制算法,电流环预测控制算法的d-q轴电流波动较小.

(a) 三相电流(PI控制算法) (b) 三相电流(电流环预测控制算法)

(c) d-q轴电流(PI控制算法) (d) d-q轴电流(电流环预测控制算法)图5 不同算法的三相电流和d-q轴电流Fig.5 Three-phase current and d-q axis current of different algorithms
电流环预测控制算法的未解耦和解耦的d-q轴电流,如图6所示.由图6可知:d-q轴解耦和未解耦的d轴电流波形在电机启动时都有波动,但解耦的d轴电流波动较小;当0.10 s突加负载时,未解耦的d轴电流有1.2 A的跳动,而解耦的电流基本保持恒定;解耦和未解耦的q轴电流基本没有变化.因此,解耦对改善电流具有一定的作用.

图7 不同算法的转速响应波形Fig.7 Rotational speed response waveform of different algorithms
PI控制算法(占空比单次刷新)的电流采样频率为10 kHz,PI控制算法(占空比双次刷新)的采样频率为20 kHz,未解耦和解耦的电流环预测控制算法的电流采样频率皆为20 kHz,载波频率皆为10 kHz.在0时刻,速度给定1 000 r·min-1的阶跃指令,不同算法的转速(ωe)响应波形,如图7所示.由图7可知:PI控制算法(占空比单次刷新)的转速响应最慢,PI控制算法(占空比双次刷新)的转速响应次之;未解耦的电流环预测控制算法的转速响应较快,解耦的电流环预测控制算法进一步提高转速响应.然而,转速响应波形在反映电流环响应快慢方面具有一定的局限性,为了更精确地分析不同算法的电流环响应速度,可以采用频域分析方法.
从频域的角度分析电流环响应,闭环截止频率越大,系统的瞬态响应速度越快.向系统电流环d轴输入幅值一定的正弦激励,通过改变激励的频率,直至幅值衰减为最大值的0.707倍,此时,激励的频率为系统电流环的带宽频率(截止频率).
在Simulink仿真软件中,向电流环d轴输入幅值为1 A的正弦激励,通过改变激励的频率分别得到PI控制算法和电流环预测控制算法的电流环带宽频率.不同算法的d轴输出响应波形,如图8所示.
由图8可知:电流环d轴输入正弦激励的频率分别为1 607,3 183,4 293,4 535 Hz,输出响应幅值均衰减为其最大值的0.707倍,解耦的电流环预测控制算法的电流环带宽最宽,响应最快.因此,从频域角度分析也可得到相同的结论.
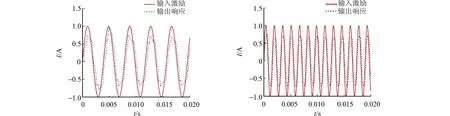
(a) PI控制算法(占空比单次刷新) (b) PI控制算法(占空比双次刷新)

(c) 未解耦的电流环预测控制算法(占空比双次刷新) (d) 解耦的电流环预测控制算法(占空比双次刷新)图8 不同算法的d轴输出响应波形Fig.8 d axis output response waveform of different algorithms
4 结束语
分析电压输出滞后、电流采样延时和d-q轴电压耦合等限制电流环带宽提高的影响因素,针对不同的延时问题,采用不同的解决方法.采用一个控制周期内占空比双次刷新的方法,改善电压输出滞后问题;采用电流环预测控制算法,改善电流采样延时问题;采用复矢量解耦控制的方法,解决d-q轴电压耦合的问题.仿真实验结果表明:相较于PI控制算法,复矢量解耦的电流环预测控制算法能够使电流环响应得到改善.

