粘弹性传动带横向非线性振动的稳定性与分岔现象

史尧臣， 李占国， 陈国平， 赵希禄

(1. 长春理工大学 机电工程学院， 吉林 长春 130022；2. 长春大学 机械与车辆工程学院， 吉林 长春 130022；3. 琦玉工业大学 工学部， 日本 深谷 369-0293)

传动带存在轴向运动且承受轴向力作用而张紧，在传动过程中会产生一定的横向振动，并导致传动平稳性降低,传动精度下降.因此，研究横向振动的动力学特性，对其振动进行控制具有很大的现实应用价值.如汽车发动机正时带是汽车中的重要组成部件，其工作性能的优劣直接影响发动机运行的平稳性,而且由于机械向高速化、精密化发展，对传动性能要求更加严格[1-3].

带传动横向非线性振动的研究范畴应归于轴向运动连续体的非线性振动.对轴向运动连续体，国外学者进行了很多研究[4-6].轴向运动弦线和轴向运动梁是轴向运动体的两个经典模型，而传动带是抗弯刚度很小的连续体，常常简化为弦线模型和梁模型来处理.当不考虑抗弯刚度时，采用轴向运动弦线模型.如Mood等[7]将传动带简化为弦线，采用摄动分析轴向运动带的振动频率、幅频特性和共振响应；Zhang等[8]建立了粘弹性传动带的受迫振动弦线模型，运用多尺度法，分析动力粘性和轴向速度对系统的影响；张伟等[9]采用两端简支的运动弦线，分析了粘弹性传动带内共振、周期运动和混沌运动.对于传动带模型稳定性研究，刘伟等[10]研究了粘弹性传动带的带速波动频率对系统稳定性的影响，给出了稳定域和不稳定域.Pakdemirli等[11]给出了轴向运动弦线的稳定域，研究得出不同阶Galerkin离散近似解下稳定和不稳定点.

目前,国内外关于传动带的研究主要集中在建立振动模型方面，对传动带的动力学特性的研究较少.本文基于轴向运动弦线模型，建立粘弹性传动带的非线性横向振动方程；然后,利用Galerkin方法离散偏微分振动方程[12-15]，研究轴向速度和带速波动幅值对系统动力学特性的影响，并分析由轴向平均速度和速度波动幅值共同决定的稳定运动区和超临界区的条件.

1 传动带横向振动动力学方程

将粘弹性传动带的传动模型简化为轴向运动的弦线[16-17].设传动带的单位长度质量为ρ，传动带的横截面积为A，v为传动带轴向运动速度，P为张紧力，c为阻尼系数，L为两简支端带的跨度，以带横向振动时的平衡位置为x轴，时间坐标为t，以带与带轮节圆切点为坐标原点，建立直角坐标系xoy，如图1(a)所示.

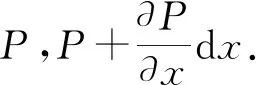
(1)

(a) 带传动简化模型 (b) 传动带微元段受力图图1 带传动的横向振动模型Fig.1 Belt drive transverse vibration model

由于传动带通常以横向振动为主，故只考虑横向振动位移产生的轴向变形，其应变的具体表达式为

(2)

当横向振动引起的轴向应变比较小，轴向应变引起的张力可用平均值替代精确值，此时张紧力为

(3)

式(3)中:P0表示带的初始张紧力；E为带的弹性模量.

对于小变形情况，有

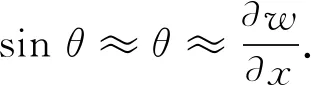
(4)

将式(2)～(4)代入式(1)中，略去dx的二阶小量，经化简可得

(5)

式(5)即为粘弹性传动带的横向非线性动力学方程.这里引入无量纲变量，即

(6)

假设传动带速度有周期波动，则有

v=v0+γsin(Ωt).

(7)

式(7)中：v0为平均带速；γ为速度波动幅值；Ω为速度波动的频率.由于γ≪1，取近似表达则有

(8)

将式(6)～(8)代入式(5)中，可得到具有速度波动的粘弹性传动带的横向非线性振动方程.即

该模型的边界条件为

(10)

2 横向振动Galerkin离散

为了研究传动带的动力学特性，采用Galerkin离散[18-19]，将振动的偏微分方程在时间和空间坐标系解耦，则方程(9)的解近似为

(11)

式(11)中:qi(t)为时间函数;sin(iπx)为模态函数.这里取一阶Galerkin离散，即

w(x，t)=qsin(πx).

(12)

将式(12)代入式(9)中，两边同乘以函数sin(πx)，并在区间[0，1]上积分,可得

(13)

式(13)表示一阶截断简化后的粘弹性传动带具有速度周期波动的非线性振动方程.

3 带传动平衡稳定性

由于

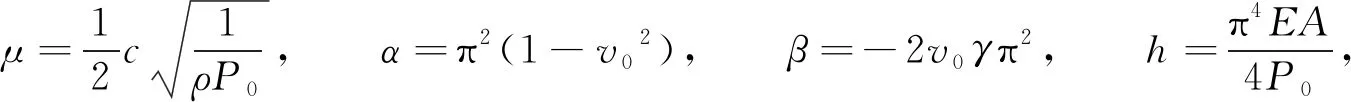
(14)

则方程(13)可改写为

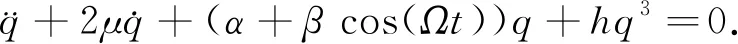
(15)

为分析系统平衡点位置及其稳定性，在相平面内分析，平衡点处速度和加速度均为零，即

(16)

选取的参数:ρ=0.12 kg·m-1，c=0.1 N·s·m-2，Ω=0.5 s-1，P0=100 N，E=0.15 GPa，A=2.78×10-5m2.现有的文献中，都是在不考虑速度波动的条件下认为临界速度为vc=1.但实际上，速度波动幅值也决定着系统的临界速度.由方程(16)可知：Δ=α+βcos(Ωt)的正负决定着系统平衡解的数目，即平均速度和速度波动共同决定着系统的分岔行为和稳定性.

对于一个振动系统的稳定性，往往会对系统的平衡点感兴趣，因为这些位置的振动状况反映着系统的分岔和稳定性；而非线性系统的稳定性可以通过判断其特征方程的根的正负来确定.

下面利用里雅普诺夫法则进行判断.令q=q1，将方程(15)降阶为

(17)

不同平均速度v0和速度波动幅值γ下系统的稳定性,如图2所示.图2中：w为无量纲位移.由图2(a)可知：系统围绕着一个稳定的平衡位置处做衰减的微幅振动，相图上表现出一个稳定的吸引子.

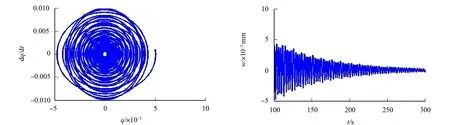
(a) 相图(v0=0.7，γ=0.15) (b) 振动响应曲线(v0=0.7，γ=0.15)

(c) 相图(v0=1.05，γ=0.15) (d) 振动响应曲线(v0=1.05，γ=0.15)图2 不同平均速度和速度波动幅值下系统的稳定性Fig.2 System stability at different average speeds and amplitudes of speed fluctuations

图3 稳定性的边界条件Fig.3 Boundary conditions of stability

平均速度和速度波动幅值共同决定的稳定性边界条件,如图3所示.由图3可知：当带速波动幅值不变时，改变平均速度的大小，传动带运动将由稳定区向超临界区转变.从图(3)还可知：临界平均速度随着速度波动幅值的增大而降低，对稳定与不稳定区的决定是最为重要的，将极大影响传动带的振动稳定性.

带传动工作时要求传动平稳，尤其对于精确传动至关重要，也更有助于降低噪音和延长使用寿命.分岔将导致系统振动不稳定.从图2可知：在稳定区域(图2(a))在初始条件激励下，系统随着时间增大做衰减振动，最后稳定在平衡位置处做幅度微弱的振动；带传动在超临界状态运动时，由于分岔而出现多周期和混沌运动，振动的幅度将会加大，如二倍周期运动(v0=0.65，γ=0.5)，最大振幅为0.012；四倍周期运动(v0=0.62，γ=0.5)，最大振幅为0.022；而系统处于混沌运动时，振幅会急剧增大，约为0.13～0.14.带速的增加加剧带传动的波动而失衡，最终有失效的可能，甚至达不到传动的目的.因此，在带传动工作时，应要求尽量消除带速波动，且工作在稳定区或弱超临界区(v0<1的超临界区域)，以实现良好的传动.

4 传动带运动系统的分岔现象数值模拟

令平均带速v0为可变参数，取带速波动幅值γ=0.5，其他值取上述基本参数值.平均带速从0.50到2.00时的无量纲振动位移和速度的分岔图，如图4(a)所示.由图4(b)可知：当v0较小时，系统做单周期振动，只有一个不动点；当v0超过某个临界值时，平衡失稳而出现周期分岔；当v0=0.62时，出现四倍周期运动.由图4(c)可知：系统有4个不动点，当v0=0.65时，出现二倍周期运动.由图4(d)可知：系统有2个不动点，根据稳定性判断条件，当γ=0.5时， 通过计算出临界值(平均速度分岔值)为vc=0.618，与分岔图中所示几乎一致，也验证了上述的合理性.由图4(c)可知：当v0继续增大，粘弹性传动带出现倍周期分岔而进入混沌运动，映射图表现为密集且有层次结构的点，表示混沌运动.

同样，令带速波动幅值γ为可变的参数， 取平均带速v0=0.80， 其他值取上述基本参数值,平均带速从0到0.80时无量纲振动位移和速度的分岔图，如图4(e)所示.从图4(e)可知：通过计算出临界值(带速波动幅值分岔值)为γc=0.225，理论计算与数值模拟结果吻合；随着参数γ的增大，系统会出现分岔现象，即由周期运动到多周期运动再到混沌运动.

(a) 平均速度分岔图 (b) 单周期运动(v0=0.62)

(c) 四倍周期运动(v0=0.62) (d) 二倍周期运动(v0=0.65)

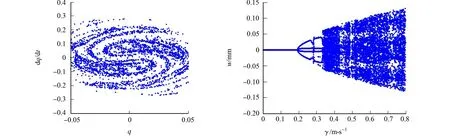
(e) 混沌运动(v0=1.05) (f) 速度波动幅值分岔图图4 分岔与映射图Fig.4 Bifurcation and mapping

由图4(a),(e)可知:随着参数的增加，系统的振动出现周期分岔而平衡位置失去稳定性，此时系统的运动变为多周期，且振幅也突然增大；随着参数继续增大，系统出现倍周期分岔而进入混沌运动.由图4(a),(e)还可知：振动响应的幅度也突然跳跃增大，此时，振幅远远大于周期和多周期运动时的振幅；在混沌区域，随着参数的继续增加，混沌运动与周期运动会交替出现，振动的幅度会发生突变，即振动的不稳定性会加剧.

5 结论

建立粘弹性传动带的积分-微分型非线性动力学方程，通过Galerkin方法离散偏微分控制方程为带有参数激励的常微分振动方程.通过轴向平均速度和速度波动幅值对系统稳定性和不稳定性的划分，两者共同决定着系统的稳定区和超临界区，给出判断的边界条件.

利用里雅普诺夫法则对系统的平衡位置的稳定性分析，表明平凡平衡位置是稳定的，非平凡平衡位置处出现分岔不稳定.利用分岔图和庞加莱映射图分析轴向平均速度和速度波动幅值对系统振动稳定性的影响，结果表明，随着参数的增大，系统由单周期变为倍周期运动，最后进入混沌运动状态.

通过观察分岔图中的分岔值点，与理论公式计算出的分岔值进行对比，二者几乎一致.这证明了划分稳定性条件的正确性，可为传动带的传动稳定性与动力学特性方面的研究提供理论依据.