椭圆界面问题的高阶差分格式
吴龙渊, 翟术英
(华侨大学 数学科学学院, 福建 泉州 362021)
1 预备知识
椭圆界面问题是一类在流体动力学、分子生物学[1]、电磁学和材料科学中广泛存在的问题.考虑如下椭圆界面问题,即

(1)
式(1)中:(x,y)∈[0,1]2,界面区域Γ={(x,y)|x=d,y∈[0,1]},边界条件为

(2)
显然,问题(1)的解在界面区域Γ上是不光滑的,甚至是不连续的.传统的数值方法已经不适用于椭圆界面问题.问题(1)的数值工作除了佩斯金的浸入边界法[2-6]之外,还有很多学者进行相关研究[7-11].此外,有限元在椭圆界面问题中也得到了广泛应用[12-14].然而,以上方法都为二阶精度.本文利用差分法构建椭圆界面问题的一个高级数值格式.在求解区域内部及界面处采用四阶逼近,在边界处应用三阶数值格式,最终得到一个具有四阶精度的数值格式[15].
2 基本引理
首先给出两个引理.
引理1假设g(x)∈C6[0,L],将区间[0,L]M等分得到一组点xi,i=0,1,2,…,M,则有

(3)

(4)
引理2[15]假设g(x)∈C6[0,L],将区间[0,L]M等分得到一组点xi,i=0,1,2,…,M.则对任意的1≤I≤M-1,有
3 数值离散


(7)
由此得到相应四阶Padé逼近[16-17],即
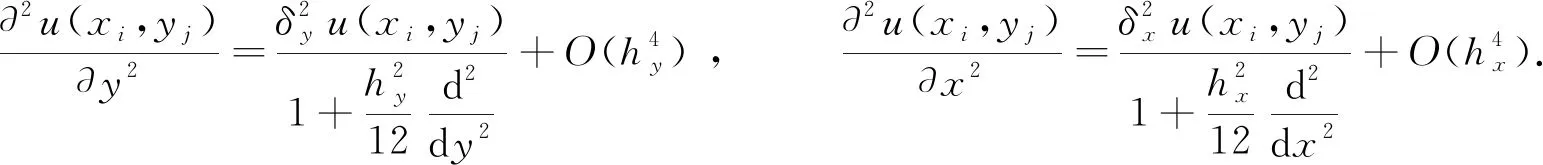
(8)
当i=1时,由引理1可知
两边同乘以Ly,则有

(11)
用数值解代替真解,省略误差项,可得
当1 (13) 特别的,当i=m时,根据式(13)可得 (14) 当i=I-时,根据引理2有 经整理可得 当i=I+时,利用引理2有 通过将式(21)和式(18)相加,可得 由问题(1)的第3式可知u(d+,y)=u(d-,y)+a(y),将其和问题(1)的第4式代入式(22)中,可得 当I- (25) 当i=M时,由引理1可知 两边同乘以Ly,则有 (28) 用数值解代替精确解并省略误差项,可得到 整理得到的格式 (30) 为验证收敛阶,选取问题 (31) 其边界条件及初值为 其中,真解为u1(x,y)=cos(πx)sin(2πy),u2(x,y)=cos(3πx)sin(2πy). 表1 算例1的空间收敛阶Tab.1 Space convergence order of example 1 (a) 数值解 (b) 真解 图1 算例1的数值图像(M=32,N=64)Fig.1 Numerical image of example 1 (M=32, N=64) 首先验证收敛阶,x,y方向剖分M,N同时扩大2倍,计算得到表1.从表1可知:随着网格剖分变细,格式的误差越来越小,收敛率也近预期的四阶精度.这说明方法是可行的.图1为算例1的数值图像.从图1可知:格式(30)可以很好地逼近真解. 为证明格式的一般性,选取如下问题 (32) 表2 算例2的空间收敛阶Tab.2 Space convergence order of example 2 u1(x,y)=x2(x-1)(x-1/2)×y(y-1)(y-1/2)·exp(x+y),u2(x,y)=(x-1)2(2-x)(x-1/2)y(y-1)(y-1/2)·exp(x+y). 首先,验证收敛阶,x,y方向剖分M,N同时扩大2倍,计算得到表2.从表2可知:随着网格剖分变细,收敛率也近预期的四阶精度.这可说明k1和k2的取值不影响格式的有效性.图2为算例2的数值图像.从图2可知:当u属于一个很小的量级时,文中的格式依然有效. (a) 数值解 (b) 真解 图2 算例2的数值图像(M=32,N=32)Fig.2 Numerical image of example 2 (M=32, N=32) 提出求解椭圆界面问题的一个高阶数值格式.数值实验验证了格式的有效性,并证明当u很小时的格式依然有效.

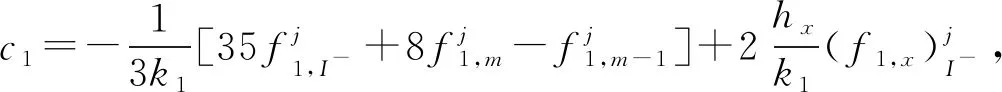





4 数值算例
4.1 算例1



4.2 算例2

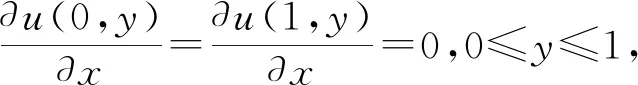


5 结束语

