广义变系数KdV方程的保角能量守恒方法
郭峰, 庄清渠
(华侨大学 数学科学学院, 福建 泉州 362021)
1 预备知识
KdV方程是一类重要的非线性模型,用于描述许多物理现象,如非谐晶体中的声波、热等离子体中的磁流体动力波及离子声波等.在各种实际物理背景中,当考虑媒介的非均匀性及边界的非一致性时,变系数模型往往比相应的常系数模型更能说明问题.考虑带依时阻尼和弥散项的广义KdV(TDKdV)方程的周期初值问题,即
ut+upux+α(t)u+β(t)uxxx=0,x∈Ω,t∈(0,T],
(1)
u(x,t)=u(x+L,t),x∈Ω,t∈(0,T],
(2)
u(x,0)=u0(x),x∈Ω.
(3)
式(1)~(3)中:p是正整数;Ω=[a,b];T是时间终点;L=b-a;u0(x)是给定的光滑函数;u(x,t)是相关波模型的振幅;α(t),β(t)分别表示依时阻尼系数和弥散系数.
方程(1)有着广泛的物理应用,如海洋动力学中的海岸波、等离子体物理学、天体物理学及流体动力学等[1-3].对于无耗散的KdV方程,已有的数值研究方法主要有有限差分法[4-5]、有限元法[6]、谱方法[7-8]等.近年来,保结构算法因能长时间保持哈密尔顿系统的几何结构而备受学者们的关注.Wang等[9]研究了无耗散KdV方程的局部保结构算法.Brugnano等[10]利用哈密尔顿边界值方法,构造了KdV方程的高阶能量守恒格式.对于具耗散的KdV方程,房少梅[11]在假设数值解有界的前提下,仅对广义KdV方程的一般谱格式和拟谱格式进行解的误差估计.Guo[12]对阻尼KdV方程提出一个保角多辛算法.目前,尚无关于阻尼KdV方程保能量耗散方面的保角保结构算法.
哈密尔顿系统最具特征的结构,就是常常被称为系统能量的哈密尔顿函数本身.由于耗散的KdV方程非哈密尔顿系统,传统的保结构方法若直接应用到此类问题就会失去其优势.针对带线性阻尼项的保角哈密尔顿系统,文献[13-16]提出能保持其保角守恒律的保角方法.本文根据这一方法,利用算子分裂技巧,对方程(1)~(3)构造一个空间上高精度的傅里叶拟谱保角能量守恒格式,该格式在周期边界条件下能保持系统的离散保角能量守恒律及保角质量守恒律.
2 TDKdV方程的保角哈密尔顿系统及保角守恒律
TDKdV方程(1)可以写成一个保角哈密尔顿系统[13,15],即

(4)
式(4)中:H为能量泛函,表达式为

(5)
保角哈密尔顿系统(4)在合适的边界条件如周期边界条件(2)下,具有以下2个保角性质.
1) 保角质量守恒律

(6)

2) 保角能量守恒律

(7)
3 TDKdV方程的保角能量守恒傅里叶拟谱方法
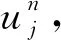
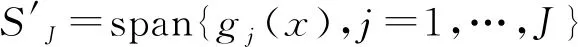
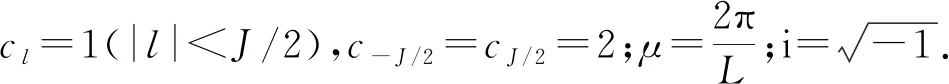

对上式求偏导,可得算子IJu(x,t)在节点xj处的s阶偏导数为

(8)
式(8)中:u=(u(x1,t),u(x2,t),…,u(xJ,t))T;Ds∈RJ×J是s阶谱微分矩阵.
D1的元素为
D2的元素为
上式中:j,l=1,2,…,J.
引理1矩阵D1的元素满足(D1)j=0,j=1,2,…,J,即D1每行元素之和为零.
证明:将u=(1,1,…,1)T,s=1代入式(8),即证明.
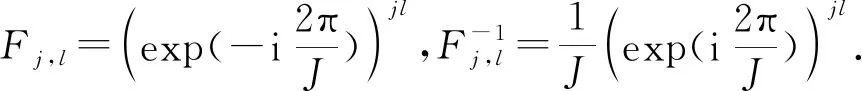
在空间上用傅里叶拟谱方法离散方程(4),得到一个半离散系统,即

(9)
式(9)中:

(10)


(11)
将空间上采用傅里叶拟谱方法得到的格式称为FPEP,采用中心差分方法得到的格式称为CDEP.
首先,将系统(9)分裂成一个保守的哈密尔顿系统

(12)
和一个耗散系统

(13)
然后,在时间方向上,应用二阶平均向量场方法(AVF)[18]求解系统(12),得
不失一般性地,设p=1,即

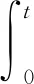

定理1式(14)具有离散保角质量守恒律,即

(16)
证明:注意到D1的反对称性,由引理1,对式(14)关于空间指标j求和,有
从而可得保角质量守恒律(16).
定理2式(15)满足离散保角能量守恒律,即
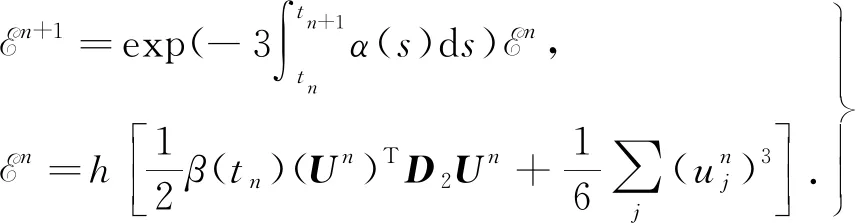
(17)

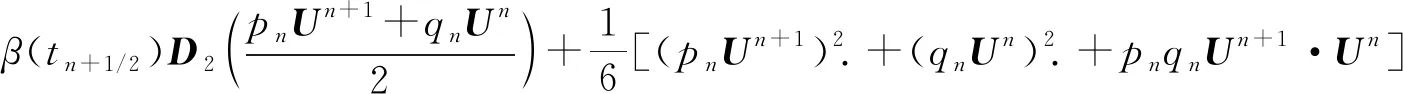

4 数值试验
对FPEP(15),CDEP(11)及下列传统AVF方法(TAVF)的解的精度、计算效率及保角守恒律误差进行比较,并考虑不同类型的阻尼对保角守恒律的影响,即
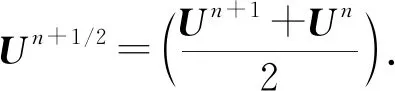
TDKdV方程(1)在p=1时,有解析解为

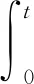
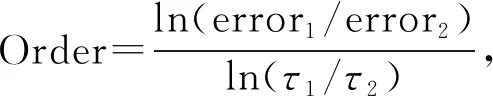
算例1设阻尼系数α(t)=0.01,当h=0.01,T=10时,FPEP和CDEP的时间收敛阶,如表1所示.τ=0.001,T=10时,FPEP和CDEP的空间误差,如表2所示.由表1,2可知:在时间方向上,FPEP和CDEP均为二阶精度;在空间方向上,FPEP的误差非常小,而CDEP的误差较大,收敛率为二阶.

表1 FPEP和CDEP的时间收敛阶Tab.1 Temporal convergence rates of FPEP and CDEP
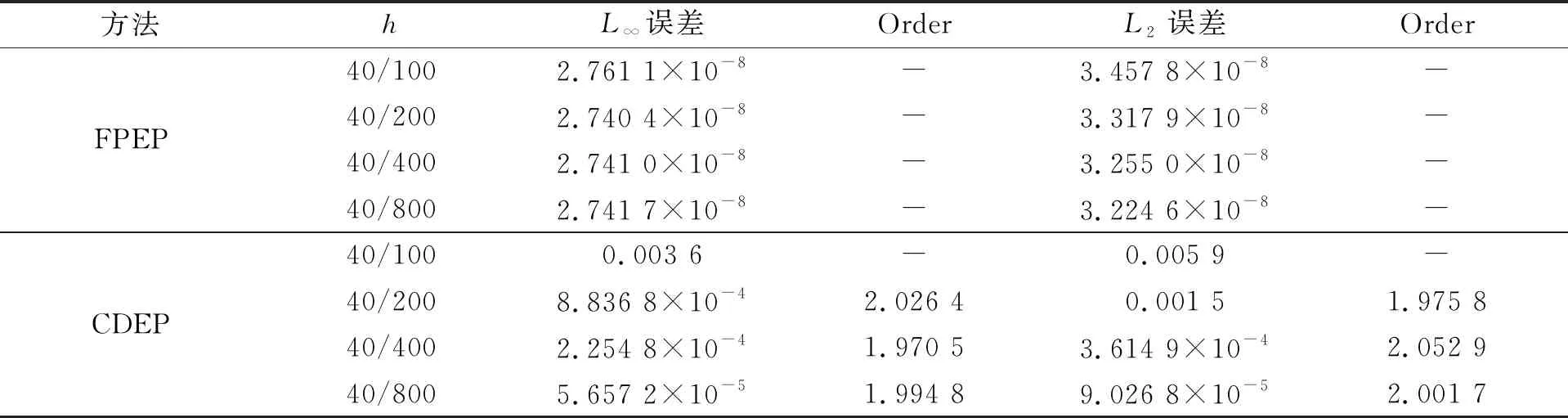
表2 FPEP和CDEP的空间误差Tab.2 Spatial errors of FPEP and CDEP

表3 不同空间步长下2种方法的CPU运行时间Tab.3 CPU times of two methods at different spatial steps s
当τ=0.01,T=10时,不同空间步长下2种方法的CPU运行时间,如表3所示.由表3可知:使用FFT技巧的FPEP的运算时间远小于CDEP.
在h=0.2,τ=0.001下,分别将3种格式运行到T=60时,其数值解与精确解的比较,如图1所示.图1中:x为空间区域.由图1可知:TAVF的误差最大;FPEP,CDEP的数值解与精确解吻合得很好.
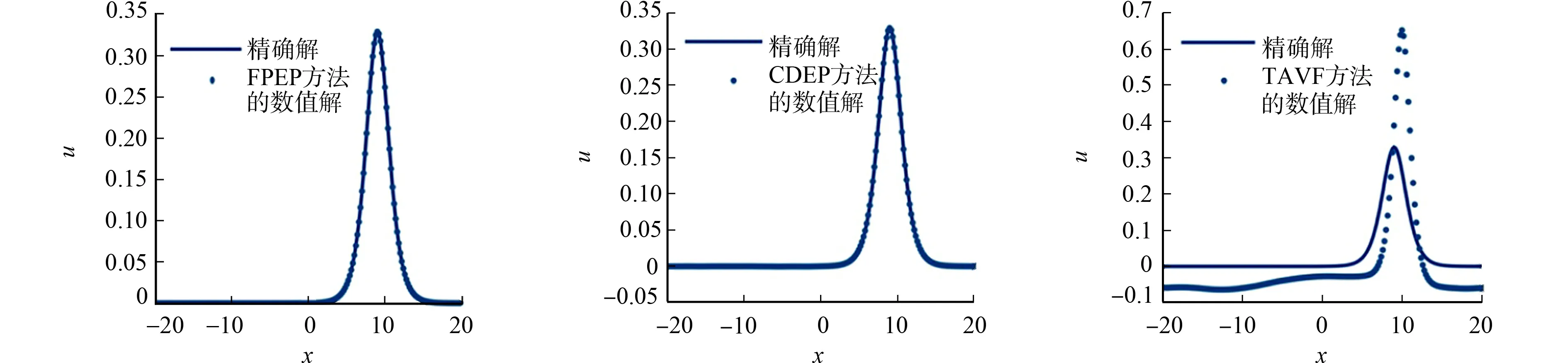
(a) FPEP (b) CDEP (c) TAVF图1 3种方法的数值解与精确解的比较Fig.1 Comparisons of exact solution and numerical solutions with three methods
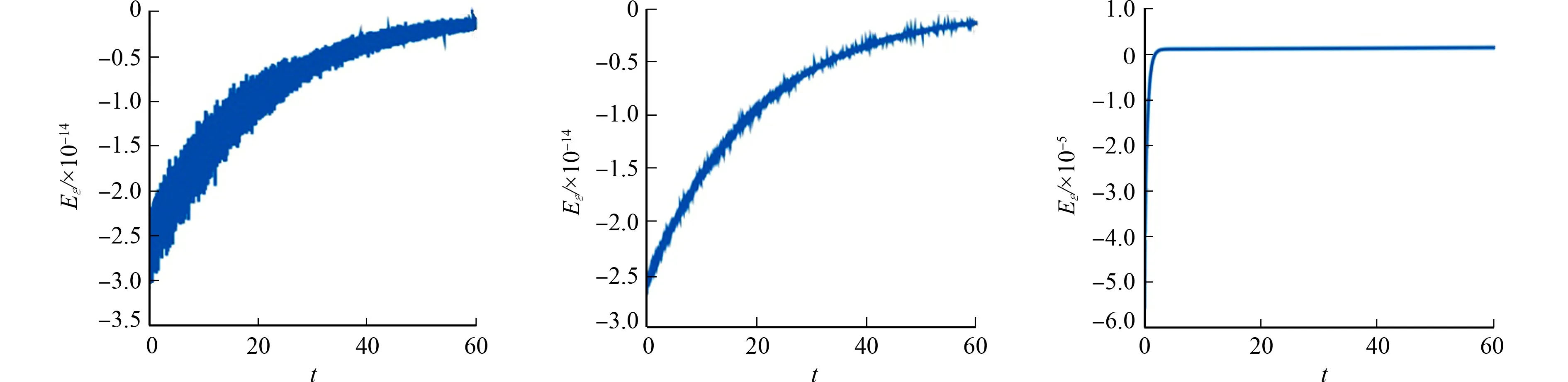
(a) FPEP (b) CDEP (c) TAVF图2 3种方法的保角能量守恒律误差Fig.2 Errors on conformal energy conservation law for there methods

(a) FPEP (b) CDEP (c) TAVF图3 3种方法的保角质量守恒律误差Fig.3 Errors on conformal mass conservation law for there methods
3种方法在时间区间t∈[0,60]上的保角守恒律误差,如图2,3所示.图2,3采用的参数与图1相同.由图2,3可知:FPEP与CDEP均满足保角能量守恒律和保角质量守恒律,而TAVF却不能满足.这表明保角能量守恒方法在保持保角守恒律方面比传统AVF方法更具优势.
算例2当h=0.2,τ=0.001时,在不同阻尼系数下,FPEP方法在时间区间t∈[0,60]上的保角守恒律误差,如图4,5所示.由图4,5可知:在不同类型的阻尼下,FPEP均能精确保持保角守恒律.
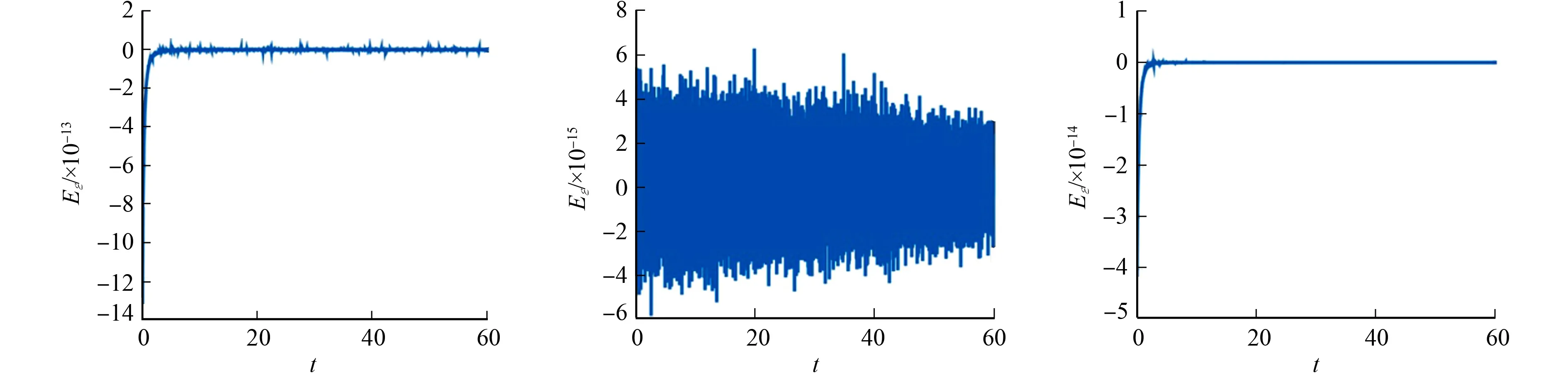
图4 FPEP方法的保角能量守恒律误差Fig.4 Errors on conformal energy conservation law for FPEP method

图5 FPEP方法的保角质量守恒律误差Fig.5 Errors on conformal mass conservation law for FPEP method
算例3阻尼系数α(t)=0.02时,FPEP方法下双孤立子的碰撞及保角守恒律误差,如图6所示.图6中:初始条件取u(x,0)=12(0.15·0.92sech2(0.9(x+12))+0.015·22sech2(2(x+8))),并假设h=0.2,τ=0.001.由图6(b)可知:双孤立子碰撞后,除了振幅减小,相空间结构仍保持良好,表明碰撞是弹性的.

(a) 双孤立子的演化 (b) FPEP在不同时刻的数值图像
(c) 保角能量守恒律误差 (d) 保角质量守恒律误差图6 FPEP方法下双孤立子的碰撞及保角守恒律误差Fig.6 Collision of two solitons by FPEP and errors on conformal conservation laws
5 结束语
时间采用二阶AVF方法,空间采用傅里叶拟谱逼近,利用Strang分裂,构造变系数广义KdV方程的一个保角能量守恒格式.计算中使用FFT技巧,不但比空间采用二阶中心差分的保角能量守恒方法误差小,而且计算效率也很高.数值实验结果表明:相比传统的AVF保能量方法,采用保角能量守恒方法更能体现保角哈密尔顿系统的本质属性,并具有良好的长时间数值行为.由于KdV方程是非线性方程,构造阻尼KdV方程在时间上更为高阶的保角保结构算法将是一个不小的挑战.

