浅谈小学奥数中的数学思想方法

杨玉旋

【摘要】本文旨在从对典型数学思想方法的叙述入手，分析小学奥林匹克数学竞赛经典例题中所蕴含的数学思想方法。进一步揭示小学奥数背后真正的教育及教学意义，明白奥数真正的存在目的——培养学生学习数学的兴趣，提高数学思维，体会数学的思想方法，培养其进行数学研究的能力以及利用数学思想及其方法解决生活实际。进一步正确地开展奥数培训及竞赛，而不是为了分数而“奥数”，也不要为了“反对”而“禁奥”。

【关键词】小学奥数;数学思想方法;小学数学教育

一、绪论

奥林匹克数学竞赛，简称奥数。1934年和1935年，苏联起头在列宁格勒和莫斯科举办中学数学竞赛，并冠以数学奥林匹克的名称，1959年在布加勒斯特举办第一届国际数学奥林匹克。而我国的数学竞赛起步也不算晚，解放后，在华罗庚教授等老一辈数学家的提倡下，从1956年起，开始举办中学数学竞赛，而全国小学数学竞赛则是在1991年开始的。

奥数的本质是为了发现和鼓励世界上具有数学天份的青少年，并让接触奥数的孩子，有一个锻炼思维和逻辑的机会。然而，近十几年来，奥数受到疯狂的追捧，奥数更是变成了升学的踏脚石，变成了家长强加在孩子身上的一座大山，变成了老师眼中的优等生标志。为了遏制这样的情况继续发生，国家和一些地方不断出台“禁奥令”叫停奥数竞赛、严禁奥数成绩与招生挂钩……

面对“奥数热”的追捧以及“禁奥令”的执行，奥数是否应该继续，社会上有着不同的声音。其实，凡事总有两面性，过度地追捧奥数，会让奥数遗失其本身真正的教育价值，而一味地反对奥数，也不免有些因噎废食之嫌。本文从以下三部分进行探讨：第一部分介绍数学思想方法的内涵及特征。第二部分介绍小学奥数中常用的数学思想方法，包括化归思想、数形结合思想、分类思想，假设思想等，并通过具体的例子予以说明。最后是对小学奥数中数学思想方法的教学的初探。作为一名教师，我们不单单要明白小学奥数中蕴含着的数学思想方法，还要懂得如何在教学过程中渗透这种思想方法，从而达到教育的目的。

二、数学思想方法的介绍

数学是客观世界中研究数量关系和空间形式的科学，数学本身包括数学知识和数学思想两个层次，数学知识是客观世界的产物，在学习数学的过程中，我们看到的，最后掌握并且可见的就是数学知识，但这仅仅是数学表面的东西。数学思想是对数学本质的认识，是数学家们从数学知识和方法中抽取出来的体现数学的内涵的东西，是数学的精髓和灵魂。数学方法是解决数学问题的一般程序，是数学思想的外在体现，故合称为数学思想方法。掌握数学思想方法对于解决数学问题，解决实际生活中的问题有着重要的意义。

数学知识固然很重要，但是对学生渗透数学思想方法更加重要，小学奥数中的数学知识对于学生来说，仅仅只是为了一次两次的竞赛需要。但其中的数学思想方法才是使学生毕生受益的关键。新世纪对于人才的要求是会“解决问题”，俗话说：“授人以鱼不如授人以渔。”让学生体会到奥数中的数学思想方法能够让学生在遇到问题时，学会利用数学的思想方法，独立解决问题，这才是奥数真正的目的，才是21世纪人才培养的目的。

三、小学奥数中具体的思想方法

在数学思想方法中，作为义务教育阶段的教学任务，一般采用基本的数学思想方法，这些基本的思想方法具有奠基性的作用，能够帮助学生在之后学习数学的过程中打下基础，并衍生出更高层次的思想方法。而小学奥数中也蕴含着许多的数学思想方法，这里重点选取几种较为基础，较为常见的进行介绍。

1.转化和化归思想

人们在面临无法解决的问题时，总是会想办法希望能够通过转化将问题变得简单，然后通过解决简单的问题来解决当前的难题。轉化和化归思想就符合人们的思维特点，将有待解决的问题X，转化为与之相关的问题Y，且Y是已经解决的或者比较简单的问题，透过解决问题Y，从而解决问题X。主要形式有：化难为易，化繁为简，化曲为直，化生为熟。

2.数形结合思想

数形结合思想是在数和形优势互补的基础上，以“形”直观地表达数，以“数”精确地研究形的思想方法。具体而言就是，在解决问题时，既分析其代数意义，又揭示其几何直观。数学家华罗庚曾说过：“数与形，本是相倚依，焉能分作两边分，数缺形时少直觉，形少数时难入微”。

将问题中抽象的数量关系与直观的图形几何结合起来，充分利用这种结合，将问题化难为易，使问题得到解决。

3.分类思想

当一个问题不能用一个标准统一解决时，常常就需要先分成几种不同的情况或种类，再制定不同情况或种类的处理规则或方法，接着再分别加以解决，这就是分类讨论思想。

4.假设思想

假设思想是先对题目中的已知条件或问题作出某种假设，接着根据已知条件进行推算，根据数量出现的矛盾，找出矛盾出现的原因，最后得到正确答案的一种思想方法。假设思想是一种有意义的想象思维，掌握之后可以使要解决的问题更形象、具体，从而丰富解题思路。

四、数学思想方法在小学奥数中的体现

1.转化和化归思想

（1）“鸡兔同笼”问题（化繁为简）

例1：今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？

分析·解：

（1）让笼子中的鸡和兔都缩起两只脚

（2）剩余脚数：94-35×2=24只因为鸡缩起两只脚后，就只剩下兔子有两只脚站立着了。故兔子的数量为24÷2=12只;鸡的数量是35-12=13只。

这道典型的鸡兔同笼的问题，历史上有多种不同的解法，而每一种解法背后就代表了一种数学思想。这里利用化归思想，化难为易，利用转化将鸡的脚数从总数中减去，使问题变得更加简单明了。

（2）“牛吃草”问题（化未知为已知）

例2：某车站在检票前若干分钟就开始排队，每分钟内来的旅客人数一样多，从开始检票到等候检票的队伍消失（还有人在接受检票），若同时开5个检票口则需30分钟，若同时开6个检票口则需20分钟。如果要使等候检票的队伍在10分钟内消失，需同时开多少个检票口。

分析·解：该题目咋看之下，会觉得文字很多，很复杂。但其实仔细精选数字，可以发现能够利用化归思想，将旅客人数看做一片草场，将一个检票口看做一头牛，便可将该题转化为“牛吃草”问题。

转化为：有一片草场，草每天生长的速度相同，若5头牛30天可将草吃完，6头牛20天可将草吃完，若要在10天内将草吃完需要多少头牛？

接着，利用“牛吃草”问题的公式，就可将题目化解。

解：将1分钟内1个检票口检票的人数当做1份，则每分钟来的旅客是

（5×30-6×20）÷（30-20）=3（份）

开始检票前有旅客

（5-3）×30=60（份）

所以，需同时打开是检票口数是

60÷10+3=9（个）

化归思想是数学中一种重要的思想和方法，在小学奥数中更是处处可见化归思想的存在，化归其实就是“转化”和“归结”的综合。体会化归思想，将复杂的问题简单化，将未知的问题转化为已知的知识，有助于学生创新精神和发散思维的发展，学生掌握了化归的思想去解决问题，可以达到举重若轻的效果。

2.数形结合思想

在小学奥数中，解决行程问题时常常借助线段图的帮助来分析数量关系;在解决一些图形的面积计算时，也常常用到画图的方法来帮助学生将数与形结合起来;甚至在简单的推理问题中也可以通过图形帮助更快捷，更简便地解决问题。

（1）行程问题

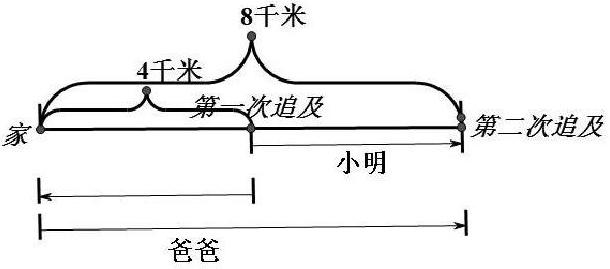
例3：上午8点8分，小明骑自行车从家里出发，8分钟后爸爸骑摩托车追他，在离家4 千米的地方追上小明。然后爸爸立刻家，回家后又立刻回头去追小明，再追上时，离家正好是8千米。假设自行车，摩托车均为匀速行驶，问第二次追上时是几时几分。

分析·解：这是一道追及的行程问题，数量关系比较复杂，小明和爸爸没有同时出发，却两次追及，使得这道题的分析思路变得复杂。如果采用数形结合思想，利用画线段图来帮助理解，将复杂的问题转化为几个简单的问题，然后逐个解决。该题中因为小明父子俩所花的时间是相同的，抓住此不变量，故可将其二人各自所行的路程表达于下列图中。

解：第一次追及后，爸爸行的路程是4+8=12（千米）

小明行的路程是8-4=4（千米）

12：4=3：1，可见相同时间内，小明和爸爸所行路程比为3：1。可将家到第一次追及地点的总距离分成3份，当爸爸出发时，小明应距第一次追及地点还有1份路程。已知小明比爸爸早出发8分钟，故小明行2份路程所用时间是8分钟。

从家到第二次追及地点的路程应为6份，得小明所需时间为：

8÷2×6=24（分钟）

8时8分+24分钟=8时32分

就是爸爸第二次追上小明的时间。

（2）推理问题

例4：甲、乙、丙、丁与小明五位学生一同进行象棋比赛，每两人都要比赛一盘，比赛中途的统计显示，甲已经塞了4盘，乙塞了3盘，丙塞了2盘，丁塞了1盘。问：小明已经塞了几盘？分别与谁赛过？

分析·解：若选择用代数方法解决此题，那么我们必须要找出其中清晰的数量关系，但是从题目中我们可以看到，唯有的几个数字之间，似乎没有什么关系，也无法列出形象的数学式子。这时我们就要考虑用几何的方法来解决啦。将五位学生设为平面上的五个点，两人之间若比赛过，则用线段将两点连接。

解：因为甲已经赛过4盘，因此甲与乙、丙、丁、小明都有线段相连（如图）;

因为丁只赛了1盘，而由图可知，丁已与甲相连，所以丁与甲赛了一盘;

因为乙赛了3盘，因此乙与甲、丙、小明等三个点都有线段相连（如图）;

因为丙赛了2盘，而由图可知，丙已有两条线段相连，所以丙与甲、乙各赛过一盘。

最后，由下图可看出，小明与甲、乙间有连线，因此小明与甲、乙各进行了一场比赛。

（3）逻辑问题

例5：有甲、乙、丙、丁四个数，甲数比乙数大7，甲数比丙数，乙数比丁数都大5， 且甲、乙两数的积比丙、丁两数的积大140，求甲、乙两数的积。

分析·解：利用数形结合思想，将题目中的数量关系转化为平面图形来研究，可以轻松将问题解决。

画一个长方形，长为甲，宽为乙，则长方形的面积为甲、乙两数的积，阴影部分为丙、丁两数的积，空白部分为甲、乙两数之积与丙、丁两数之积的差140。

解：由图所知，

140-5×5=115

115=5×23=5×（丙+丁）

丙+丁=23

∵甲-丙=5，乙-丁=5，且甲-乙=7

∴丙-丁=7

丙=（23+7）÷2=15

丁=15-7=8

∴甲×乙=（15+5）×（8+5）=

20×13=260

由以上例子可以看出，数形结合思想在解决实际问题中的重要性，当面对题目中的数量关系比较复杂，且利用代数方法无法求出时，可以考虑转化为几何图形;或者将几何图形抽象出代数式子来解答。数形结合思想对于学生的发散思维能力，智力等都有极大的促进作用，运用得当时，甚至会给人一种“柳暗花明又一村”的效果。

3.分类思想

（1）“排列组合”问题

例6：用五张数字卡片：0，②，④，⑥，⑧，能组成多少个不同的三位数。

分析·解：运用分类思想，因为最高位数不为0，故可以按0所在位置分为三类：

第一类：十位数字是0，则有4×3=

12（個）

第二类：个位数字是0，则有4×3=

12（个）

第三类：个，十，百位上都不为0，则有4×3×2=24（个）

一共有12+12+24=48（个）

（2）抽屉原理

例7：任意给出5个两两不相同的整数，请说明其中必有两个的差是4的倍数。

分析·解：因为任意一个整数除以4，余数有4种可能：0，1，2，3。因此可以运用分类思想，将5个整数，分成4种类型，也就是构造4个抽屉：除以4的余数分别是0，1，2，3。根据抽屉原理，其中必有一个抽屉中有两个数，且这两个数除以4的余数相同。可设这两个数为4m+1和4n+1（m，n都是整数）。它们的差为4（m-n），必为4的倍数。

（3）平面几何问题

例8 下图中共有多少个长方形

分析·解：在面对该题时，许多学生一开始都会一个一个地数，但这样就很容易会遗漏或者重复。而为了能够做到不重不漏，最好的便是采用分类思想，将长方形分成几种类型，之后分别进行计算。

解：单一的长方形：3×3=9;

由两个单一长方形组成的长方形：横数2×3=6，竖数2×3=6，6+6=12;

由三个单一长方形组成的长方形：横数1×3=3，竖数1×3=3，3+3=6;

由四个单一长方形组成的长方形：4;

由六个单一长方形组成的长方形：4;

由九个单一长方形组成的长方形：1。

共计 9+12+6+4+4+1=36（个）

分类思想是小学数学中较为重要的思想之一，应用也很广泛。分类思想有利于学生养成有条理地思考，培养全面思考和良好的数学思维品质。采用分类方法，可以让学生从宏观到微观地进行分类学习，做到不重不漏，既能把握全局，又能抓住细节，有助于形成系统的数学知识结构。

4.假设思想

小学奥数中，体现假设思想的内容比比皆是，例如在逻辑问题中可以通过假设，让问题变成更加明朗，便于入手;而在经典的鸡兔同笼问题中，较为经常的也是运用假设的方法予以解决。

（1）“逻辑问题”中的假设思想

例8：“希望杯”考试结束后，小军和小楠对班上5名同学的名次进行了猜测。小军的猜测：小军第一名，小明第二名，小华第三名，小光第四名，小楠第五名;小楠的猜测：小华第一名，小光第二名，小明第三名，小楠第四名，小军第五名。考试成绩出来后，实际上，小军的猜测都不对，不但一个名次没对上，而且相差一个名次的都没有，小楠猜对了一个人的名次，那么五个人的实际名次是怎样的？

分析·解：依题意，可知，小军只可能是第三、四、五名;小明只能是第四、五名;小华只能是第一、五名;小光只可能是第一、二名;小楠只能是第一、二三名。因为小楠猜对了一个名次，所以，小明第三名，小楠第四名是错误的。但还是无法知道小楠的猜测中“小华是第一名、小光第二名、军第五名”中哪个猜测是对的。因此，这时就可以利用假设思想来解答。

①假设“小军第五名”是正确的，则“小华第一名”是错误的，故小华只能是第五名，但与“小军第五名”矛盾，故假设不成立;

②假设“小华第一名”是正确的，则“小光第二名”是错误的，故小光只能是第一名，但与“小华第一名”矛盾，故假设不成立;

③假设“小光第二名”是正确的，则“小华第一名”是错误的，“小华是第五名”，可推得“小明第四名、小军第三名、小楠是第一名”。

综上所述，可得五个人的名次如下：小楠第一名、小光第二名、小军第三名、小明第四名、小华第五名。

（2）“鸡兔同笼”问题中的假设思想

例9：今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？

解：假设鸡有35只，则总脚数为

35×2=70（只）

但实际上总脚数为94，比实际少了

94-70=24（只）

因为把兔子算成了鸡，把一只兔子算成一只鸡，少算了2只脚，一共少算了24只脚，就少算了24÷2=12（只）兔子，故兔子的数量为12只。

35-12=23（只）

所以鸡的数量为23只。

五、小学奥数中数学思想方法的教学初探

小学奥数是为了给学生渗透数学的思想方法，而基本途径就是教学。教师要在教学的过程中学会如何在教授基础知识，讲解解题过程中教给学生数学的精髓，让学生体会到数学的思想方法，从而达到应用。

1.充分挖掘小学奥数中的数学思想方法

数学知识是客观地，显性地体现在书本上的，但数学思想是隐形的，是学生无法简单地察觉到的。因此，在教学中，我们要善于挖掘小学奥数教材中所含的数学思想方法。化隐为显，结合基本的数学知识，让学生在潜移默化中体会数学思想，学会掌握数学方法，养成数学能力，从而达到培养学生数学素养的目的。例如，在例题1中，要能够明白采用“金鸡独立”的方法，目的是为了让学生体会化归思想，那么在教学该例题时，就应该引导学生学会转化，学会寻找化难为易的桥梁。假如授课教师无法意识到这点，仅仅只是将该方法教给学生，那么这道题就失去了其价值。

2.在思维活动中，揭示数学思想

在小学奥数的教学过程中，要让数学思想暴露出来。让学生清楚知道现在在学习的是什么样的数学思想，有什么内涵，有怎样的特征，能够帮助解决怎样的问题。新课改要求，在教学过程中要体现学生主体性，假如学生连自己学习的是什么都不知道，那么谈何掌握，只有让学生知道现在自己是利用什么思想方法在解决问题，那么才能够真正体会到该思想方法并予以应用，才有助于学生形成数学素养。例如，在教学例题4时，应该让学生明白运用了数形结合的思想方法，为什么要采用這样的方法，而同样一道题，例题1采用化归思想，例题4采用数形结合思想，它们各自的优点是什么，在什么情况下可以采用数形结合思想，又如何运用。

3.在探索过程中激活数学思想