追问，让数学思维向更深处漫溯

蒋亚燕

[摘要]问题是思维发展的砥砺石，更是学生数学素养不断积累的关键点。为此，在日常教学中教师应利用追问诱发学生联想，使学生的数学思维更加开阔，并设计合适的体验情境，促使学生的学习理解更加深刻，从而实现思维的飞跃，促进他们综合素养的不断提升。

[关键词]追问;数学思维;数学素养

[中图分类号]G623.5 [文献标识码]A [文章编号] 1007—9068（2019）32—0035—02

数学教学的主要任务不仅是基本知识、基本技能的传授，更重要的是促进学生积累丰厚的数学活动经验，发展学生的数学思维，从而使其具有发现问题、提出问题、分析问题、研究问题的能力。学生的数学学习是一个富有创造性的过程，所以通过追问引领学生进行学习和反思，势必会使动手实践、自主探索和合作交流等数学学习活动更具活力，也会促使学生的数学思考有效发散，向纵深处漫溯，让数学学习充满情趣，闪烁着智慧的光芒。

一、诱发联想，追问使思维开阔

积极的联想是有效数学学习的利器之一。当学生能够依据眼前的学习内容联想到相关联的知识点或学习活动过程，那么他们的思维也会随着联想而灵活开阔起来。因此，在数学教学中，教師要找准每一个知识点的来龙去脉，科学地进行预设，并设计有序的知识阶梯，促使学生能够感受到知识的生长点，从而进行合情的、有效的联想，使既有的知识、经验、技能、思维方法等成为有效学习的敲门砖，成为终身学习的基本积累。

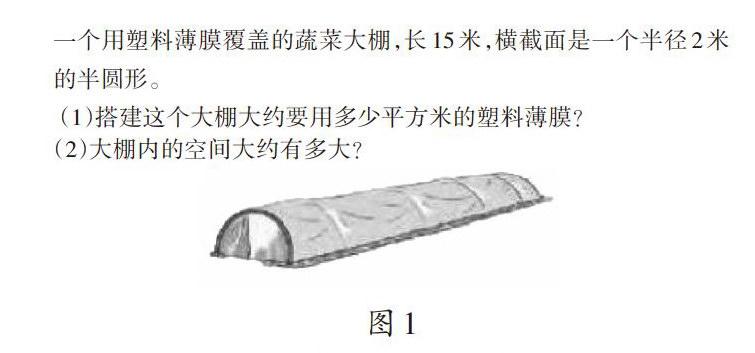
如在“圆柱的表面积和体积”练习课中，教师出示书中的习题：

师：你能根据题目中的数据去解决问题吗？（学生自主练习，并进行交流）

生₁：搭建大棚需要的薄膜面积就是大棚的表面积，对应圆柱表面积的一半。

生₂：对！前后的半圆相当于圆柱上下底的一半，顶棚的薄膜相当于圆柱侧面积的一半。

生₃：体积也是圆柱体积的一半。

生₄：我看到过这样的一道习题（如图2）：（1）给这个积木表面涂油漆，要涂的面积是多少平方厘米？（2）这个积木的体积是多少立方厘米？它和刚才的大棚的计算方法一样吗？

（看到学生的问题，教师首先引导学生自主思考，再引导小组进行辨析。）

生₅：计算体积的方法一样，都是计算圆柱体积的一半。涂油漆要求表面积，这里的长方形面积是要计算的，而大棚的地面是种蔬菜的，不需要铺薄膜，所以两者的表面积计算方法不一样。

师：你的分析很到位，很准确。对于这个积木的体积，你有其他的思考吗？

生₆：可以横向对等切开，再拼起来，就是一个底面直径为10厘米、高为10厘米的圆柱体了。

有效追问，能够诱发学生展开联想，使其数学思维向更广阔处延伸。案例中教师的追问，使得大棚的体积与所用薄膜的面积的特征愈加明显，不仅能促进学生对相关知识的回顾、运用和积累，同时还丰富了学习的内容，开阔了学生的认知视野，让学生在比较中发现知识的异同，在研究中获得更丰富的感知，有效地帮助学生建构数学认知。

二、以用促思，追问使思维深刻

数学学习的目的是积累知识经验，形成技能技巧，发展数学思维，但最终目的是使学生能够运用知识技能去发现问题、研究问题和解决问题，从而实现思维的发展。因此，教师要引导学生进行必要的数学练习，使其在练习中学会思考，学会梳理总结，进而获得重要的数学思想方法，使数学思维在训练中变得愈加犀利、深刻。

如“找次品”的教学片段：

师：经过上面的研究和学习，老师想了解大家的数感水平，看看谁的反应快、思考深。在27个同样的零件中有一个次品是偏轻的。给你一个天平，至少称几次保证能找出次品呢？

（学生进行小组讨论）

生₁：要4次，27→（13、13、1）→（6、6、1）→（3、3）→（1、1、1）。

生₂：3次就可以了，27→（9、9、9）→（3、3、3）→（1、1、1）。

师：大家看看，谁的思考更有道理？

（学生再次比较两个同学的称量过程，得出结论——至少3次）

师：27个零件只要3次。如果是81个这样的零件中也有1个次品呢？

（学生运用获得的经验去思考）

生3：4次就够了，81→（27、27、27）→（9、9、9）→（3、3、3）→（1、1、1）。

师：这么少的次数啊！还记得刚上课时，大家讨论2187个零件中有1个次品需要称几次，有同学说需要2185次。现在，你是怎样想的呢？

（学生讨论，得出只要7次：2187→（729、729、729）→（249、249、249）→（81、81、81）→（27、27、27）→（9、9、9）→（3、3、3）→（1、1、1））

生₄：我发现要使得称的次数最少，应尽可能平均分成3份。

纵观整个教学活动，执教者匠心独运。课前，以猜猜2187个零件来热身，在繁杂的数据刺激下让学生的思维预热起来;课始，通过3个零件的实践称量，得出（1、1、1）分法，再拓展到9个零件。面对9个零件，不同的学生会有不同的思考实践，当“9→（4、4、1）→（2、2）→（1、1），3次”和“9→（3、3、3）→（1、1、1），2次”等不同的思路呈现时，学生通过比较，深刻地体会到“至少称几次”的基本要义和优化策略的价值。课中，教师引导学生解决上述案例中的几组问题，使得优化策略深深烙印在学生的脑海中。

教师有意识地引导学生运用在9个零件中找出次品的经验和方法，去思索27个零件、81个零件的情况，最后照应到上课前的热身思考题的2187个零件，使数学思考呈现阶梯性，让学生在问题突破中感受到思考的魅力。其间教师的不断追问极具活力，一个又一个富有思考性的问题被抛出来时，学生的惊讶、感叹与震撼之情也随之而来，学生被数学的神奇魅力所感染，从而使数学学习具有了更强的挑战性和趣味性，无形之中使学生的数学思维获得质的飞跃。

三、以评激思，追问使思维敏捷

发挥评价的激励作用，以此促进学生的思维发展，也是有效教学策略之一。适宜的、恰当的评价，能够改善课堂的质态，有利于学生积极思考，提升学生思维的灵活性，使得学生数学思维向更深处漫溯有了基础。

如“三角形的面积公式推导”教学片段：

师：刚才计算了长方形、正方形、平行四边形的面积，那图3的面积，你会求吗？

（学生看到图形，提出不同观点）

生₁：这是个三角形，它的面积计算公式还没有学过。

生₂：老师，三角形的面積计算是不是我们今天要学习的内容啊？

师：是的！我们今天会研究三角形的面积计算。你能运用长方形、正方形或平行四边形的面积计算方法先思考一下吗？

（学生积极思考，动手操作）

生₃：我把正方形沿对角线剪开，得到2个一样的三角形，所以三角形的面积等于正方形面积的一半，即边长乘边长除以2。

生₄：我把长方形剪成两个一样的直角三角形，其中一个三角形的面积等于长方形面积的一半，即长乘宽除以2。

生₅：平行四边形也可以剪成2个一样的三角形，因为平行四边形的面积等于底乘高，所以我们先要找准三角形的底和高，发现它们与平行四边形的底和高重合。这样一个三角形的面积就等于底乘高除以2。

师：老师发现了一个有趣的现象，大家得出的三角形的面积都要除以2，这是为什么呢？

生₆：我们都是把图形一分为二，那么得到的三角形的面积只是原来图形面积的一半。

师：对的。那能不能反过来进行一种新的尝试呢？

（学生在教师的追问中，进行尝试性操作）

生₇：我们小组发现用2个完全一样的三角形可以拼成一个长方形、一个正方形或一个平行四边形，可见一个三角形的面积就是拼成图形面积的一半，所以三角形的面积等于底乘高除以2。

评价是学习的催化剂。如果教师能够掌控好这一利器，就一定能开启学生的心扉，增强学生的学习信心，也会激活学生的学习思维，让数学课堂洋溢着无尽的活力。案例中教师不惟教材的编排，而是顺势利导，引导学生用既有的图形面积计算过程去想象，以获得最直接的感知。同时，利用恰当的评价，激励学生去思考，“老师发现了一个有趣的现象，大家得出的三角形的面积都要除以2，这是为什么呢？”这句话既肯定了学生的活动成果，又给学生开启了一扇新的思考之门。因此，在数学教学中，教师要时刻关注学生的学习质态，多站在学生的立场上去审视学生的活动。长此以往，学生就有信心去发现问题，有勇气去提出问题，也会更加缜密地思考，精心组织语言来表达自己的所思所想，思维也会随着学习的深入而不断深刻。

综上所述，用好课堂追问这一利器，能够促使学生对学习更为关注，促进其独立思考的深入，诱使其学习灵感的萌发，更是改善课堂学习格局、激活学生思维，逼近知识本质内核的“导火线”。因此，在数学教学中，教师应敏锐地发现、捕捉生成信息，善假“意外”因素巧追问。同时，还要引发学生的有效追问，让他们在追问中学会思考，在思考中开启智慧、引发创新。长此以往，学生的思维会在追问中迈向更开阔的“原野”！

（责编 罗艳）