真问题·真研究·真收获

潘智

[摘要]在小学数学教学中，教师依靠问题与学生进行互动和教学。合理的问题能更有效地提升数学教学质量，促进学生思维的发展。从一道易错题入手，有针对性、有层次性、有启发性地设计问题，借助结构化问题，引导学生深入探究，使学生达到理解算理、运用算法的学习目的。

[关键词]结构化问题;余数;优化算法

[中图分类号]G623.5 [文献标识码]A [文章编号] 1007—9068（2019）32—0008—03

所谓结构化问题，即在数学课堂教学中，以学生的知识经验和现有数学能力为基础，构建的一套有针对性、层次性和系统性的问题组。这里的“结构化”有两层含义：一是环环相扣、层层递进，问题之间有关联性，用以有序激发、指导学生的数学探索活动;二是指问题有深度和广度，在问题组的设计中，紧紧围绕核心问题，纵向和横向均有效发散，最后又回归核心问题，促进学生构建完整的知识体系，提升学生的思维品质，发展学生的核心素养。本文以苏教版教材四年级上册“两、三位数除以两位数”的单元检测中，学生的一道易错题为例，探讨如何在教学中应用结构化问题激起学生的研究热情，激活学生的研究潜力，激发学生的探索精神。

一、核心问题为起点

数学教学活动必须建立在学生已有的知识经验和认知发展水平之上，任何问题的提出也要以此为基础，才能避免成为无源之水、无本之木。有道是“良好的开端就是成功的一半”，好的问题能激发学生的興趣，使学生产生好奇心和求知欲。同样，好的问题也应抓住知识的本质、触及知识的核心。因此，无论在何种情境之下，都要让核心问题成为起点，让学生站在自己的知识结构之上开展数学活动。

在“两、三位数除以两位数”的单元检测中有一题“108÷28”，此题的本意是让学生用竖式进行计算，小华同学却运用简便计算方法：

108÷28

=108÷4÷7

=27÷7

=3……6

这里利用了一个运算规律：a÷b=a÷c÷d（其中6=c×d）。4×7=28，所以108÷28=108÷4÷7没错;因为108÷4=27，所以108÷4÷7=27÷7也没错;27÷7=3……6同样没问题！但是正确的余数是24，究竟问题出在哪里？小华不解，所有人都觉得不可思议。

这不是教材中的内容，却是数学学习中的“真问题”。这个问题的核心就是对算理的理解，产生两种结果的原因就在于它们的算理不同。因此，我向学生提出了本次研究中的第一个也是核心的问题：“这样的算法合理吗？小华同学能解释你做法的合理性吗？”一石激起千层浪，学生的好奇心、好胜心被“点燃”，他们纷纷说出了自己的观点和想法：

“我觉得余数是错的，但是又不知道怎么说明。”

“我认为小华的算法是合理的，可余数为什么是6还是要通过生活中的例子来说明一下。”

“是的，除法就是平均分，我们可以用东西分一分啊！”

“108太多了，到哪里找这么多东西去分呢？”

提出问题后不一定立刻就要有答案，教师应该为学生提供一定的自主思考与探索的时间，使大部分学生都能经历问题的解决过程，从而真正成为学习的主人。因此，我让学生课后开展探究，可以与同学或父母进行合作，也可以自己动手试一试。

果不其然，第二天小华自己就有了发现：

“昨天同学们提醒我，除法就是平均分，可以拿108个物体来分一分，但是这么多数量的东西不好找，所以我就想到了用108粒米来分。”

“我和爸爸首先根据108÷28的平均分意义，每28粒分一份，共分成了3份，还剩24粒，余数确实是24。”

“接着按我的简便算法来平均分，108÷28=108÷4÷7，先把108粒米平均分成4份，每份是27粒，再根据第二步算式‘27÷7将每7粒米分一堆，这样每一堆都可以分成3份，剩6粒。”

“将两次的结果一对比，就很容易发现：其实按照简便计算的方法，最终剩下的总的余数（不在圆圈里的）也是24，余数6只是其中一份的余数，一共有4份，每份都余6粒米，所以正确的余数就是4×6=24。”

“我写的6应该叫小余数，24才是大余数啊！”

“小余数”——这个名字真不错！学生利用数形结合的方式探究核心问题，阐述了自己的算理与算法，提出“小余数”的概念，完成了真研究的起始工作。

二、关联问题显维度

提问就像是点亮明灯，能指引学生学习的方向，可探索知识的道路还是需要学生自己去寻找，实践操作就是他们寻找的工具。在学生探索知识的道路上，这盏明灯所能照到的地方越多，学生的思维就越广阔，思维品质就越能得到有效的锻炼。这时，要依靠从核心问题引申出的、有层次性的、有针对性的多维度问题，帮助学生明晰算理、厘清思路、拓展方法。

为了对“小余数”进行“真研究”，我引导学生从以下几个问题开始探究。

问题一：每一个这样的计算都会有“小余数”吗？“小余数”和“大余数”之间有联系吗？

“我们列举出这么多算式，它们两种计算方法得到的余数确实都不一样，一个大的，一个小的，真的有‘大余数和‘小余数之分了。”

“‘小余数虽然不是正确的余数，但是分米粒时已经说得很清楚，所有的‘小余数加起来就是‘大余数。我认为遇到有余数的题目完全可以用这样的简便方法进行计算，只是最后要把‘小余数乘第一个除数才能得到‘大余数。

108÷28=3……24.

108÷28=108÷4÷7=27÷7=3……6：

252÷32=7……28.

252÷32=252÷4÷8=63÷8=7……7：

570÷35=16………10，

570÷35=570÷5÷7=114÷7=16……2;

999÷12=83……3，

999÷12=999÷3÷4=333÷4=83……1。

如6×4=24、7×4=28、2×5=10、1×3=3等，道理也很简单，因为‘大余数是按照第一次除法的份数去平均分的，所以第一次的除数是几，‘小余数就有几份。”

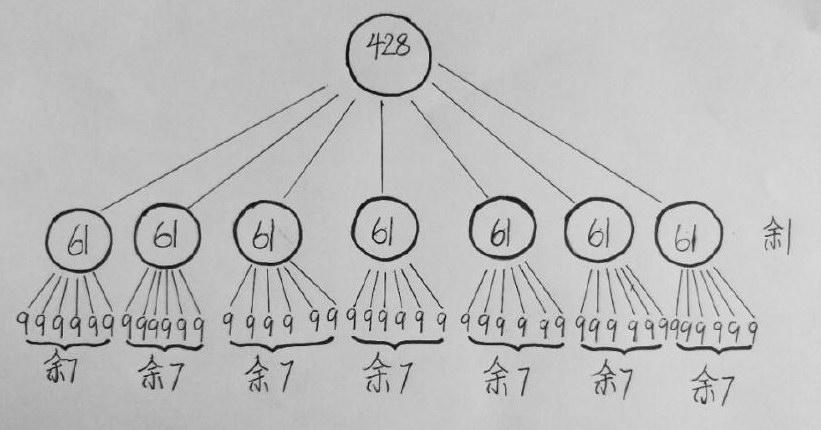
问题二：有的小组举例428÷63=428÷7÷9，可是第一步计算428÷7时就有余数，像这样第一步就产生余数的算式，还能简便计算吗？如果能，“小余数”和“大余数”之间又有怎样的关系？

第一次研究时，有近一半的小组遇到了同样的困难，只是他们及时更换了数据。新的问题让他们重新回到深度研究之中。虽然有点难度，但是学生很快还是有了发现，如图：

“这是根据小华的分米粒想到的办法，我们小组尝试画图来表示。从图中可以看出，先算428÷7将428平均分成7份，每份是61，余数为1;接下来应该将7个61都按每9个一份进行平均分，每个61都可以平均分成6份，余7个。因此最终商为6，余数一共有7×7+1=50，这答案与用竖式计算的结果是一样的。”

“其实就是正常一步步地计算，只不过第二次计算时是用第一次得到的商继续除，余数先放到一边，最后还原成‘大余数时，一定要把这个第一次得到的‘小余數加上。”

“我们小组一开始写的1001÷32也可以简便计算。我口算了一下，先算1001÷4等于250余1，把‘小余数1放一边，再算250除以8得到31余2，那么‘小余数2乘4再加1等于9，最终的答案就应该是31……9。”

“老师，我在想，刚才都是把一个除数变成两个除数，能变成三个、四个除数吗？”

瞧，水到渠成后，学生代替教师提出了更深层次的问题。

问题三：像375÷24这样的算式，能变成375÷2÷3÷4加以计算吗？借助“小余数”能算出正确的“大余数”吗？

没多久，更复杂但是又很有条理的算理图就被学生画了出来，如图：

“根据我们研究出的方法，先算375÷2=187……1，‘小余数1放一边记下;再算187÷3=62……1，这里的1乘2后也记下;接着再算62÷4=15……2，我把这里的2叫作“小小余数”，要用2×2×3=12记下;最后用三次得到的1+2+12=15，得出375÷24=15……15。”

学习数学知识不仅要理解其核心问题，更重要的是要理解各知识点之间的关联，以便于形成立体式的知识结构。三次探讨“小余数”和“大余数”关系的过程，是层层递进提问、步步剖析算理的过程。这几个问题循序渐进，指引学生思维不断发展。学生通过动脑、动手和动口，探究算法，经历了知识的形成过程，积累了活动经验。

三、优化问题有收获

比较是促进思维发展的重要手段，对比可以帮助学生找出知识之间的差异与联系，提高学生的观察能力、思维能力、运算能力等。尽管学生在操作中掌握了算理，但是算法的对比和优化不能忽略，这将是提高学生运算能力的有力保障。

“这样的计算方法与竖式计算相比，你更喜欢哪一种呢？为什么？”这个问题让学生开始了新的讨论，他们交流各自答案并说明理由，有的学生仍喜欢竖式计算，有的学生觉得小华的方法更简单，可以直接口算，也有的学生表示都喜欢，要合理使用。这时，可安排学生共同出题，并分别用两种方法进行计算比赛。通过计算比赛，学生感受并验证每种方法的优势与不足，达到优化算法、提高运算能力的效果。

算理是本次研究的核心问题，是问题的开始，也应该是问题的延续。根据学生的掌握情况，我又提出了新的要求：“既然这两种方法都合理，那么它们的结果怎样才能表示成同样的形式？”这个问题直指算理本质，目的是进一步拓展学生的思维深度：有的说直接写3……24，有的说可以用3……6×4表示，还有的想到了小数。经过讨论，大家一致同意用小数表示更合理，且尝试用计算器计算了108÷28和108÷4÷7=27÷7的最终答案，发现显示的结果都是相同的。于是大家又计算了其他算式加以验证，并在此基础上进一步明确：进行平均分时，剩下的余数还可以不断地分下去，就产生了小数，只不过小数计算还没学到，但是可以用计算器证明无论是竖式计算还是简便计算，如果一直平均分下去，最终的结果都是一样的，所以这两种方法都是正确的。

学生在数学学习中会产生许多疑问，正如小华的错解带来的疑惑，这时教师就可以开展数学活动，引导学生借助生活经验去尝试、去发现。每一次活动都应该从问题开始，同时产生新的问题，并不断探索下去，最终找出问题的本质，获得真理。一道常规的竖式计算题，却因为一位学生的简便计算而让知识间产生了交集，其中的错与对使学生对知识有了新的感受，产生了真问题;师生带着问题进行思考与探索，在经历数学活动的过程中，创造出了“小余数”这个闻所未闻的新概念;层层递进的结构化问题让学生的思想发生碰撞，分与合的双向思维成功提高了学生的运算能力;同时，问题火花的飞溅使得内容不断丰富、问题意识不断延伸、智慧研学不断开花结果。面对学生认知的新问题，教师要有效设计问题，舍得花时间、愿意给空间，让学生开展真研究，去触摸知识的本源、探寻思维的路径、提升学习的品质，实现真收获！

（责编 金铃）