用好问题引领儿童数学学习

李瑾

[摘要]好的问题能引领儿童数学学习，促进儿童深度思考。通过对专家和新教师课堂教学中的提问进行对比和分析，发现好问题一定指向“数学学科本质和核心价值”，蕴含“学习方式与理解路径”，且能激发儿童的“探究热情和欲望”。

[关键词]好问题;儿童;数学学习

[中图分类号]G623.5 [文献标识码]A [文章编号] 1007—9068（2019）32—0003—03

问题是儿童学习的目标、动力和途径，问题引领儿童学习数学的过程，让学生从知识的接受与获得，转化为亲身体验“知识的生成和建构”，并促进儿童进行深度思考，从而获得数学成长。好的问题将能引领学生学习的发生和深入，那什么是能引领儿童数学学习的好问题呢？我们工作室的教师一方面关注自己课堂教学中的问题设计，同时也尝试对比专家和新教师在同一课题下的课堂提问，探寻好问题的共性。

【案例1】“认识平均数”（苏教版教材四年级上册）

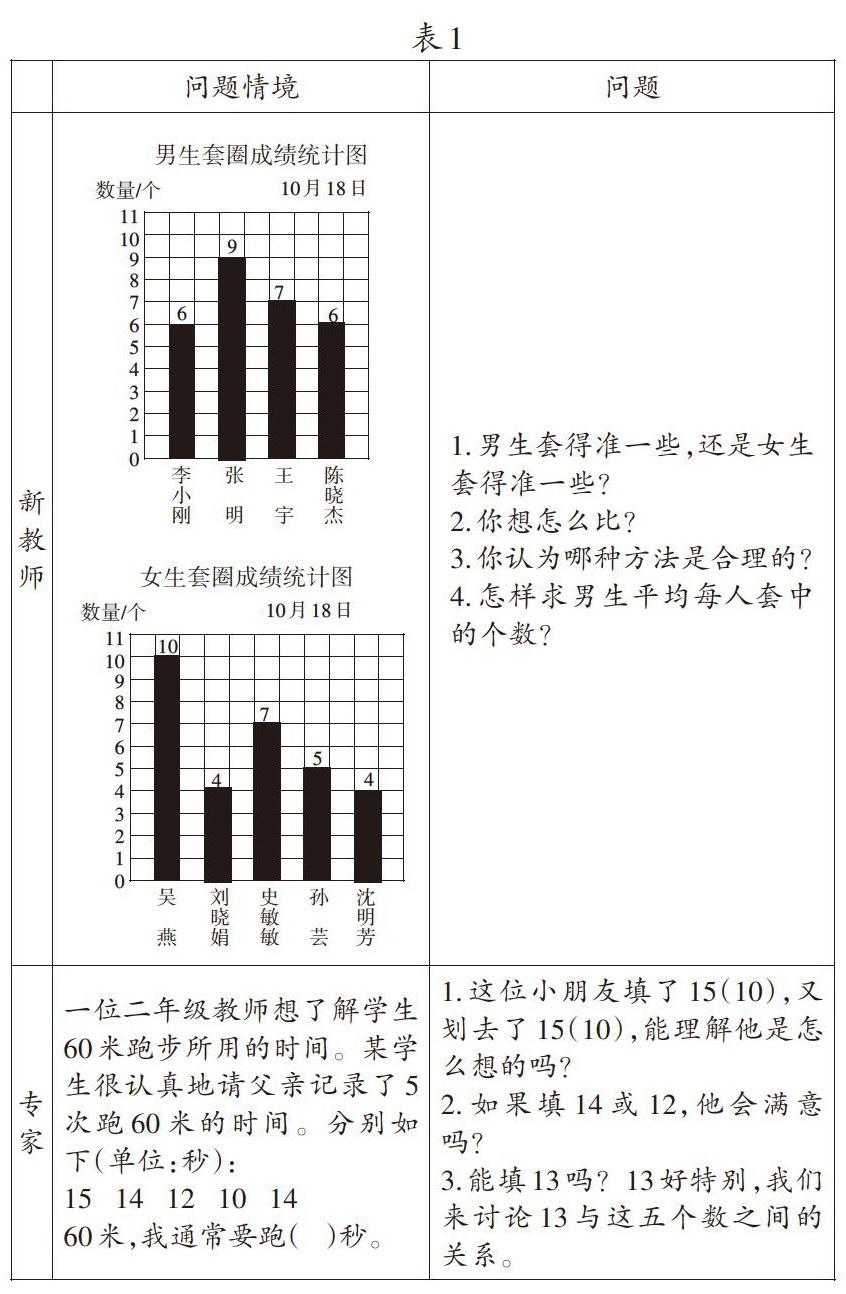
一、案例呈现（如表1）

二、案例分析与思考：好问题应指向数学学科本质和核心价值

1.對问题的分析

平均数可以把一组数据作为一个整体进行描述，是小学阶段“统计与概率”领域中唯一一种统计量。要完整理解平均数的意义，需要理解两个要点，即平均数描述了一组数据的整体水平，以及平均数具有虚拟性。

对平均数的概念及其内涵了解之后，进一步分析新教师和专家所给出的问题。

新教师所提出的4个问题中，前3个问题指向的是什么情境下使用平均数，第4个问题指向的是平均数的计算方法。概括起来就是“情境”与“公式”，即今后遇到类似情境就运用这个公式，是通过重复的应用帮助学生形成解题的能力。

专家在“问题情境”中提出的一个大问题“60米，我通常要跑（ ）秒。”，直接指向寻找一个能代表一组数据整体水平的数，即平均数的代表意义。其后给出的三个问题都是引领学生对平均数的代表意义做出思考与讨论。尤其是13与五个数之间的关系，既包含了平均数的虚拟性特征，又蕴含了平均数的计算方法。概括起来就是通过合适的问题情境与问题促进学生感受并自主构建平均数的概念及对要点的理解。

2.思考：好问题应指向数学学科本质和核心

由上述分析可以看出，新教师与专家在设计问题的过程中都关注到了儿童的已有经验和教学目标，但新教师所设计的问题容易使学生对概念的理解出现缺失：学生知道平均数有什么作用，怎么得到，但是却不知道平均数到底是什么。而专家给出数据后所引出的问题“60米，我通常要跑（ ）秒。”情境相对复杂，但是直接指向了数据分析，能够引领学生有意识地从数据的角度思考有关问题，尽管这个时候还没有学平均数的意义和求法，但是学生寻找可以代表一组数据整体水平的数据的过程，实际上已经指向平均数的意义，这种自发的、非正式的认识，无疑有助于学生更好地构建平均数的概念，以及体会这个统计量的作用。

正如张奠宙教授认为，一个好问题要能体现数学本质，具有数学价值，能够启发学生进行深度的数学思考。即教师需要分析和发掘教学内容与目标所包含的核心问题，并围绕其提出供学生研究和思考的问题，而新教师恰恰在对数学概念本质的理解上与专家存在差异。因此，要寻求这样的好问题，教师不仅要关注教材，更重要的是理解与掌握教材内容中的数学知识本身，这样才能发掘更多指向数学学科本质核心与价值的优质问题。

【案例2】“认识面积”（苏教版教材三年级下册）

一、案例呈现

二、案例分析与思考：好问题应蕴含学习方式与理解路径

1.对问题的分析

面积概念的意义建构需要学生调用已有的生活经验，并在操作活动中不断感受，从而使得学生对面积意义的理解更加全面。新教师和专家都调用了学生已有的生活经验，但是新教师认为学生的经验是“面是有大小的”，因此给出的问题均是从面的大小出发，让学生通过比较两个面的大小，初步理解面积的含义，最后运用面积概念进行比较。“唤起经验——得出概念——进行运用”是从教的角度给出的理解路径。

专家所提出的问题也是基于学生的经验基础，但不忽略学生在生活中对面积的有所了解，从“在哪里听说过？”和“你有什么问题？”开始了解学生的现实起点，然后让学生通过描线和涂色的操作对比（实质上是周长和面积的比较），初步感知什么是面积，最后再回到生活中感受什么是面积。这是一条“现实起点出发——与相关概念对比学习——回到生活深入理解——完成概念建构”的理解路径。

2.思考：好问题应蕴含学习方式与理解路径

运用数学的思维方式进行思考，学会数学地思考，是问题解决中明确提出的培养学生创新意识和实践能力的目标，也是决定数学课程改革方向的基本载体。从学生熟悉的情境开始，运用问题解决的路径，如上述面积概念的建构中，专家提出的问题中就蕴含“数学现实——对比学习——逐步数学化——概念建构”的理解路径。尤其是在相关概念的学习过程中，通过对周长和面积形象化的感知，学生不仅建构了面积概念，也再次完善了周长概念。

在上述理解路径的基础上，专家提出的问题还有利于学生之间的对话、合作与反思。像这样蕴含学习方式和理解路径的问题，需要把握住儿童数学现实与学科课程目标之间的距离，而实现这一距离的跨越就是设计合理丰富的学习方式与符合儿童心理的理解路径，以达到用数学任务和设计的数学问题帮助学生“学会思维”的目的。

【案例3】“表面涂色的正方体”（苏教版教材六年级上册）

一、案例呈现

二、案例分析与思考：好问题能激发儿童的探究热情和欲望

1.对问题的分析

在“表面涂色的正方体”一课中，学生需要想象出把大正方体的每条棱平均分成3份并切开，小正方体表面涂色的不同情况及每种小正方体的个数和位置，从而为后面的规律探索奠定基础。

兩个课例情境相仿，都是先呈现一个表面涂色的大正方体（每条棱都平均分成了3份），然后提出问题。

新教师给出的问题中，“3面涂色、2面涂色、1面涂色的各有多少个？分别在什么位置？”及后续的第3个问题，看似给了学生主动探究的机会，但实际上是教师指令性的观察与操作，学生始终处于接受指令、被动思考与探索的状态之中，无法激起学生探究的欲望。

专家通过掉落的大正方体，提出了“如果把大正方体复原，你会吗？”这种具有挑战性的游戏任务，能够满足学生对游戏天然的喜爱，可以点燃他们主动观察、操作的热情火花，而在复原失败后，因为不服输精神，探究与思考成为他们内在的需求，教师提出的反思性问题（复原的过程中遇到了什么困难）与提示性问题（这里的小正方体一共有几种？不同的小正方体分别在什么位置？各有多少个？）为他们指明了探究的方向，激发了他们探究的欲望。

2.思考：好问题能激发儿童的探究热情和欲望

问题，尤其是具有数学任务的问题，是启发学生开展数学思考的核心动力，但是若无法吸引学生参与讨论则会失去其价值与意义。一个好的问题，对每个个体而言都是独特的，让每个学生都可以参与到其中进行思考。如上述专家给出的“复原”任务与问题，看似并没有提出观察每个小正方体，实际上，“复原”任务中包含着对正方体的观察，及其所处位置的思考。因其游戏的形式，使得每个学生都可以参与其中，容易激起学生思考的欲望，并引发学生之间的讨论，同时又有向纵深发展的余地。

张奠宙教授在好问题的标准中提出的第一条就是要能引人入胜，激发学习者思考的欲望，因此能够激发儿童的探究热情和欲望的好问题就是数学思考的良好开端。我们在把握学科本质的基础上需要多研究儿童，研究他们的天性和心理规律，以寻找与儿童现实及学科本质相匹配的问题，激发儿童的探究热情和欲望。正如华应龙老师在《好课如初恋般美好》一文中谈到，“几何是和想象力玩耍的玩具”，课上学生还没有玩起来，还没有玩够，教师就匆匆忙忙揭示规律，仓促“登堂入室”，就像一个小孩尚未长大，你就要他承担大人的角色，那是操之过急了。数学中可以玩的元素很多，应该从生动、有意思，及玩好数学的角度设计好问题，以此激发儿童进行探究。

从以上所呈现的案例和分析可以看出，新教师与专家所设计的问题具有差异性，专家设计的问题情境与问题往往指向学科本质与核心价值，蕴含着丰富的学习方式与理解路径，能激发儿童的探究热情与欲望。文中每个案例的分析虽然仅涉及其中某一个角度，而好的问题往往同时兼具三个方面的特征，三者之间的关系如下图所示：

通过对比不同教师所设计的问题，能引发我们对“好问题”的思考，并进一步探寻如何设计“好问题”。教师要加强对数学学科本质的掌握与理解，更新儿童观，并以学习路径作为沟通学科与儿童之间联系的桥梁，深入理解三者之间的关系，从而设计出“好问题”来引领儿童的数学学习。

（责编 金铃）