以《事件的独立性》教学设计为例， 谈数学核心素养

熊慧玲

[摘  要] 核心素养背景下，高中数学教学案例的设计，需要将数学学科核心素养的六大要素，与具体的教学环节联系起来，思考每一个环节可能对数学学科核心素养的培育起着什么样的作用. “事件的独立性”是高中数学概率知识的重要组成部分，与学生的生活具有一定的联系. 从具体的实例中进行抽象，然后通过逻辑推理建立模型，并在问题解决的过程中强化知识理解，是有效构建数学知识，实现核心素养落地的重要途径.

[关键词] 高中数学;核心素养;教学案例设计;事件的独立性

数学核心素养是具有数学基本特征的、适应个人终身发展和社会发展需要的思维品质与关键能力. 《普通高中数学课程标准》（征求意见稿）明确指出：数学核心素养是数学课程目标的集中体现，是在数学学习的过程中逐步形成的. 高中阶段数学核心素养包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析. 这些数学核心素养既有独立性，又相互交融，形成一个有机整体[1]. 从理论的角度来看，高中数学学科核心素养是自洽的，符合逻辑的，这一点毋庸置疑. 而从实践的角度来看，一线教师最关心的是高中数学学科核心素养如何从理论变成可操作的步骤. 很显然，这个步骤首先体现在教师的教学设计上，而根据笔者的经验，在理解一个新的学习理论的时候，最佳的方式就是选择一个案例进行深度研究，在研究的过程当中不断地吸纳理论知识，不断地对可能发生的教学实际情况进行预测，这样往往能够促进对理论的理解，也能够对实践产生真正的指导作用. 我们仅以高中数学“事件的独立性”教学案例的设计为例，谈谈笔者的思考.

■以生为本，理解数学学科核心素养

核心素养是面向学生的核心素养，高中数学学科核心素养的六大要素是面向学生需要的培养目标，因此，在理解学科核心素养的时候，必须坚持以生为本的教学理念. 只有确定了这一出发点，才能让学科核心素养的培育落到实处. 高中数学是高中所有文化学科的基础性学科，其对培养学生的思维能力、思维习惯，具有不可替代的作用. 高中数学事件的独立性这一知识，与学生的生活有着密切的联系，但是学生在生活当中体验事件的独立性的时候，往往是基于生活经验而非严密的逻辑推理，因此，在学生学习这一知识的时候，是会遇到不少困难的. 有同行发现：有些学生特别容易混淆新旧概念，又因所求事件与已知事件相互关系较复杂，刚开始学习时很可能掉进各事件间的“蜘蛛网”，茫然找不到头绪[2]. 其实在笔者的教学当中，也遇到过这种情况. 因此本节课的教学，很容易将教学的重心确定，即在梳理其逻辑关系以及概率知识上. 问题在于，如果只重视其中的逻辑关系以及概率知识，那么学生学习的时候会感觉十分的抽象，影响其学习兴趣不说，其学习结果也不会很好.

在核心素养视角下，笔者发现本课的教学可以另外寻找一个重心，那就是学生的能力培养，或者说素养培养. 尽管素养和能力不是同一个概念，但是在面向学生，想让学生知道通过本节课的学习可以获得的一些素养的时候，不必过于强调能力与素养的区别. 也就是说对于学生而言，我们告诉他们是在为了培养他们的能力，而在教师的教学目的当中，教师应当知道是为了培养学生的学科核心素养. 这就是“以生为本”理念的体现.

从数学知识逻辑的角度来看，理解事件的独立性，需要让学生理清概念. 数学上将“事件的独立性”定义为“一个事件的发生对另外一个事件发生的概率没有影响”，其概率公式为P（AB）=P（A）·P（B）. 其经常与另外两个事件进行对比、学习. 一是互斥事件——不可能同时发生（当然有可能都不发生）的事件，其概率公式为P（A+B）=P（A）+P（B）;二是对立事件——两个不可能同时发生的事件，而且是A事件发生的时候，B事件必不发生，反过来，B事件发生的时候，A事件必不发生，其概率公式为P（A+B）=P（A）+P（B）=1.

这样的定义与比较，对于学生来说，绝大多数情况下是感觉到比较抽象的. 抽象的原因是因为学生的大脑当中没有形象的事件作为支撑. 因此，从核心素养培育的角度来看，这里的教学设计可以通过给学生提供形象事件的方法，让学生对事件的独立性的理解有表象可以支撑，同时还可以培养学生的数学抽象能力，而数学抽象正是数学学科核心素养的重要组成部分;至于数学学科核心素养中的逻辑推理，在本内容的教学当中更是非常丰富;而建立起来的对事件的独立性的理解，本身就可以作为一个数学模型在其他的场合使用. 因此在事件的独立性这一内容的教学中，数学抽象、逻辑推理、数学建模非常充分，而根据史宁中教授的观点，有了这三个方面，数学学科核心素养的培育就可以得到保证了.

■内容导向，实现教学案例高效設计

确定了学生是学习的根本，那么在事件的独立性这一教学中，教学设计需要坚持的另一个思路，就是内容导向. 也就是根据数学知识发生的逻辑去设计教学，当然，这一设计过程中，对学生认知规律的把握是不可缺少的. 实际上这一点早就有人提出，比如有人认为：将高中数学的“六大核心素养”培育有效地融入数学教与学的过程中，落实到教育的主体（学生）身上，成为目前数学教学亟待解决的重要工作，甚至可以说是教育教学的核心工作[3]. 笔者在设计这一课的时候，重点设计了三个方面：

一是帮学生回顾条件概率的知识. 实践表明，在概率知识的学习中，如果忽视了对基础的把握，那么学生构建新的概率知识就比较困难了. 事件的独立性这一知识的学习与条件概率的知识有着密切的关系，所以必须让学生非常熟悉条件概率. 关于这一点，本文不再赘述.

二是给学生提供生活案例，让学生去辨别分析. 笔者提供的例子有：在篮球比赛过程当中，通常有罚球. 那“第一次罚球进了”与“第二次罚球进了”这两个事件有没有互相影响？在一个不透明的箱子当中有三个颜色不同而其他都相同的球，其中两个球是白球. 如果采用不放回的取球方式，那么“第一次任取一个球是白球”，与“第二次任取一个球是白球”，这两个事件有没有互相影响？在一个不透明的箱子当中有三个颜色不同而其他都相同的球，其中两个球是白球. 如果采用放回的取球方式，那么“第一次任取一个球是白球”，与“第二次任取一个球是白球”，这两个事件有没有互相影响？

这三个例子都是学生比较熟悉的例子，因而学生的思维容易加工，而在这个环节学生思维加工的时间短，就可以保证其可以将自己的注意力集中到对事件的互相影响的判断上来，从而保证学生的思维围绕“判断两个事件的相互独立”而展开. 事实证明，学生基本上能够做出正确的判断，即第一种和第三种情况是互相独立的，而第二种不是互相独立的.

这样的话，学生对“事件A是否发生对事件B是否发生的概率没有影响”就容易产生理解，这种理解是不需要付出太多努力的，因为有事例的支撑，他们几乎可用自己的直觉去进行理解与判断，这会进一步理解独立事件的性质而奠定坚实的基础. 由于第一点对条件概率的知识进行了回顾，这里建立P（AB）=P（A）P（B）也就不会遇到太多的困难.

三是理解相互独立事件的性质. 实践表明，对独立事件的性质的理解，可以在比较中进行. 这涉及的事件通常有互斥事件、必然事件、不可能事件、任何事件，等等. 当然，这里要注意的是，只有学生对其他事件相对比较熟悉的情况下，他们才能在比较的过程当中更好地理解独立事件的性质.

■问题解决，学生对学习内容精加工

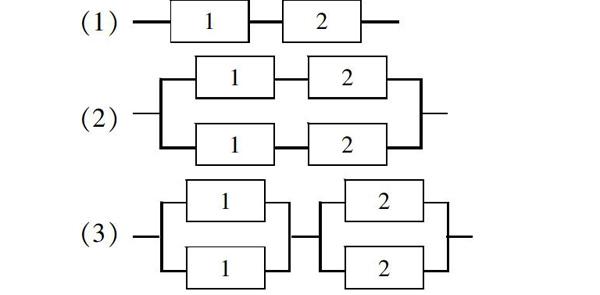
问题解决是巩固知识的重要途径，问题解决也是核心素养体现的重要环节[4]. 在事件的独立性这一内容的教学中，笔者设计的问题也来源于生活. 比如，一个电子元件正常工作的概率r称之为这个元件的可靠性，由多个元件组成的系统正常工作的概率称为系统的可靠性. 假如每个元件工作的可靠性都是0

（1） ■

（2） ■

（3） ■

这个例子具有学科融合的特征，需要学生通过逻辑推理去判断各个系统的组成形式，进而思考事件独立性的性质，在本问题的解决当中起着什么样的作用. 当学生能够将事件的独立性的限制与此问题解决进行良好的结合时，通常可以认为学生的逻辑推理是成功的，对事件的独立性这一数学模型的掌握是成功的.

总的来说，学科核心素养背景下设计高中教学案例，需要将数学核心素养的要素与具体的教学内容对应起来，然后重点设计培育这些素养内容的环节，做到这一点，就邁开了核心素养培育的第一步.

参考文献：

[1]  张先龙，肖凌戆. 基于数学核心素养的教学设计——以函数的单调性新授课为例[J]. 中学数学教学参考，2017（z1）.

[2]  赵苏琴. 找准目标 对症下药——谈怎样理解事件的独立性[J]. 新高考：高二数学，2015（04）.

[3]  庄志刚，于莺彬. 基于高中数学核心素养的教学设计研究与实践[J]. 数学通讯，2017（24）.

[4]  胡先富. 事件独立性的教学中应该注意的两个问题[J]. 数学通讯，2003（23）.