巧用情境 突出研究 落实素养
庞海燕


[摘 要] 文章是作者参加金华市高中数学优质课比赛所创作的《数学建模——体重与脉搏》教学设计,旨在同时铺开建模线和研究线的思路指导下,让学生经历和体验数学建模的全过程,落实数学建模核心素养.
[关键词] 数学建模;体重;脉搏;研究
■教学内容与核心素养解析
本课选自《普通高中数学课程标准》中的数学建模教学案例28(P156-P159).数学建模是高中数学的一条主线.教材在各个学习内容的开始,普遍从实际问题出发提出问题,引出知识,让学生感悟数学源于实际;学习了数学的概念、定理和公式之后,从数学模型的角度加以理解并应用数学模型解决实际问题,让学生学习和应用数学模型(比如必修1中《函数模型及其应用》). 《体重与脉搏》一课主要通过建立体重与脉搏的数学模型让学生经历和体验数学建模活动全过程,感悟数学源于实际,学习和实践数学建模,学习和应用数学研究.
数学建模是对现实问题进行抽象,用数学的语言表达问题、用数学方法构建模型解决问题的素养. 数学建模过程主要包括:在实际情境中从数学的视角发现问题、提出问题,分析问题、建立模型,确定参数、计算求解,检验结果、改进模型,最终解决实际问题. 通过高中数学课程的学习,学生能有意识地用数学语言表达现实世界,发现和提出问题,感悟数学与现实之间的关联;学会用数学模型解决实际问题,积累数学实践的经验;认识数学模型在科学、社会、工程技术诸多领域的作用,提升实践能力,增强创新意识和科学精神.
数学建模是一种独立的数学素养,却又是一种综合程度最高的素养,因为建模的过程离不开抽象概括、逻辑推理、直观想象、数学运算、数据分析.
■教学目标和目标解析
本节课旨在通过创设情境,从具体的、确定数据出发,通过实验研究、文献研究、机理研究多角度、逐层把情境中的问题,通过拟合、假设、简化、发现、表达、提炼和抽象得出“比例模型”,得到一个合理的函数关系,利用找到的函数模型解决实际问题.在这一过程中让学生体验数学建模和研究方法,提升学生的数学建模能力,即阅读理解能力、抽象概括能力、符号表示能力、模型选择能力、数学运算能力. 激发学生学习数学的兴趣,培养学生主动探索的精神以及团结协作的品质.
根据上述分析,制定本节课的如下内容.
教学重点:通过情境,让学生经历和体验数学建模的过程;
教学难点:分析模型,厘清问题,对模型进行假设和简化;
教学关键:以经历“体重与脉搏”模型建立为明线,讲应用;以模型研究为暗线,立素养.
■教学问题诊断分析
数学建模教学就是教师与学生一起经历将生活数学化,再数学生活化的过程. 平时的数学应用题都是经过加工、提炼、简化的数学模型,学生习惯于思考和求解已经“数学化了”的问题,不会将实际问题数学化、抽象化.
本节课的学生面临的难点并不是模型的建立和求解本身,而是问题是具有生物学背景,学生感觉比较陌生,涉及的量比较多,需要厘清量之间的关系,对问题进行简化和假设. 学生往往抓不准问题中的量,不会也不习惯“机理分析”,理不清思路,写不出函数关系,不会把实际问题转化为数学问题.
■教学支持条件分析
在前面的学习中,学生已经学习了指数函数模型、对数函数模型、幂函数模型、三角函数模型,对函数模型建立有初步认识,理解有实际背景和意义的函数图像,会选择适当的函数类型构建数学模型,但把实际背景数学化的过程中,通过什么样的方式帮助学生厘清量之间的关系,做出简化假设是值得思考的.
模型的数据拟合需要借助MATLAB软件,限于现阶段技术和硬件支持,课堂上只呈现了结果,没能让学生亲历编程拟合.
根据上述分析,制定同時铺开研究线、建模线,采取科技引路、问题驱动、引导为辅、活动为主、自主探究、合作交流的教学策略.
■教学过程
引趣——课前活动
学生活动:自测脉搏率.
一、激活——情境创设
情境创设:
师:用数学的眼光观察世界,用数学的语言描述世界,用数学的思维思考世界,用数学的模型把握世界. 很高兴和我们武义一中的同学们一起共享今天的数学建模活动. 为了更好地了解世界,人们常常用数学(如函数或方程)来描述某种特定的现象,称为数学模型.生活中处处可见数学模型.远到医学CT层析仪,电视数字化、华为的突围、讯飞翻译机,近到我们的脉搏率,我们可以如何测量脉搏率呢?
生:中医的望闻问“切”,西医的仪器辅助.
师:老师今天不用切脉,不用仪器,我要通过一个数学模型,你只要告诉我体重,我就可以算出脉搏率,将这样一个生活问题数学化,可以实现吗?
生:面面相觑.
师:今天我们一起来研究体重和脉搏率的数学关系.我们可以如何开展我们的研究呢?
学生活动讨论.
师:经过同学们的讨论,一方面我们可以通过实验研究,收集动物体重和脉搏率的数据,对其进行分析研究;另一方面可以通过研究文献,科学地认识生物学背景知识,再通过数学机理研究,给出体重和脉搏的量化关系.
二、建模——模型建立
(一)实验研究
下表给出了一些动物体重与脉搏率对应的数据.
生:从图中可以看出,体重越轻的动物脉搏率越高.
师:如果想要用体重预测脉搏率,可以如何操作?
学生活动:讨论得出可以建立体重和脉搏率的函数模型.
教师简要介绍数学软件MATLAB的线性和非线性拟合功能.根据课堂情况决定是否比较模型选择(见附件2).
图3
师:图2是用MATLAB软件拟合的函数模型f=1831.5W-0.302.
豐富学生的学习方式、改进学生的学习方法是高中数学课程追求的基本理念. 学生的数学学习活动不应只限于对概念、结论和技能的记忆、模仿和接受,独立思考、自主探索、动手实践、合作交流、阅读自学等都是学习数学的重要方式. 本节教学中,既有教师的讲授和引导,更多的是学生的自主探索与合作交流,整节课教师都通过活动创设,让学生积极参与,给学生适当的拓展、延伸的空间和时间,激发学生对数学建模的兴趣,养成良好的研究、学习习惯.
附件1
体重与脉搏
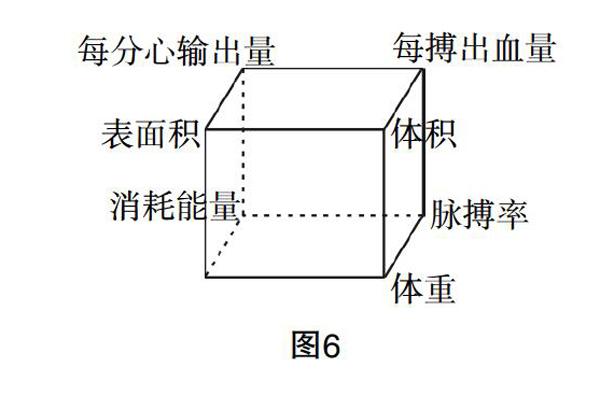
问题的提出:生物学家认为,睡眠中的恒温动物依然会消耗体内能量,主要是为了保持体温.研究表明,消耗的能量E与通过心脏的血流量Q成正比;并根据生物学常识知道,体温主要通过身体表面散失,动物的体重与体积成正比.
1. 请根据生物学常识,给出血流量与体重之间关系的数学模型;
2. 从表中可以看出,体重越轻的动物脉搏率越高. 请根据上面所提供的数据寻求数量之间的比例关系,建立脉搏率与体重关系的数学模型;
3. 根据表格,作出动物的体重和脉搏率的散点图,验证建立的数学模型.
生物学背景阅读材料
脉搏率f:指动脉搏动的频率. 脉率的快慢受年龄、性别、运动和情绪等因素的影响. 成人每分钟超过100次,称为心动过速,每分钟低于60次,称为心动过缓.临床上有许多疾病,特别是心脏病可使脉率发生变化.因此,测量脉率对病人来讲是一个不可缺少的检查项目. 中医更将切脉作为诊治疾病的主要方法.
脉率是每分钟脉搏的次数,正常情况下与心率一致,与呼吸的比例约为4∶1~5∶1.
健康成人在安静状态下脉率为60~100次/min,女性稍快.
脉率受年龄和性别的影响,婴儿每分钟120-140次,幼儿每分钟90-100次,学龄期儿童每分钟80-90次,成年人每分钟70-80次. 另外,运动和情绪激动时可使脉率增快,而休息时则减慢. 发烧时,人体的脉率会有所增高,一般每增多20下,相应体温会增高1摄氏度左右.
成人每分钟超过100次,称为心动过速,每分钟低于60次,称为心动过缓.临床上有许多疾病,例如发热时心动速度也会加快,特别是心脏病可使脉率发生变化.因此,测量脉率对病人来讲是一个不可缺少的检查项目. 中医更将切脉作为诊治疾病的主要方法.
心输出量Q:心脏的功能就是输出血液,推动血液流向各组织器官,以保证新陈代谢的正常进行,心输出量是衡量心脏工作能力的重要指标. 正常情况下,每个心室收缩一次所射出的血量,称为每搏出血量,每搏出血量q与心脏大小成正比,心脏大小与动物的体积V成正比.每分钟射出的血量称为每分出血量,即每搏输出量与每分钟心率的乘积. 通常所说的心输出量是指每分输出量.?摇 动物体安静时的心输出量Q和基础代谢一样,与体表面积S成正比.
散热能量E:早在十九世纪末年,生理学家Voit氏等发现虽然不同种类的动物每千克体重单位时间内的散热量相差悬殊,但如都折算成每平方米体表面积的散热量,则基本一致.
例如马、猪、狗、大鼠和人的每体表面积每24小时的散热量都在1000卡左右,散热量与体表面积成正比.
附件2:原始数据取对数后拟合情况

