凸多边形内的“费尔马点”问题

北京市海淀区水木龙华培训学校 张靖华

对于三角形内的费尔马点问题的讨论已屡见不鲜，本文将给出凸多边形内的一点到相邻三顶点距离之和的最小值的计算公式。

定理1：在凸多边形A1A2…An中， 若 (∠ AiAi+1Ai+2， ∠ Ai+1Ai+2Ai，∠Ai+2AiAi+1)max＜120°，则△AiAi+1Ai+2内有且只有一点，使得PAi+PAi+1+PAi+2之和最小，且最小值为：

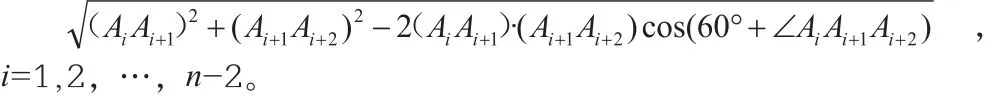
证明：在凸多边形A1A2…An中，相邻三顶点Ai，Ai+1，Ai+2构成的△AiAi+1Ai+2中，满足(∠AiAi+1Ai+2，∠Ai+1Ai+2Ai，∠Ai+2AiAi+1)max＜120°，由费尔马命题知：

在△AiAi+1Ai+2中存在一点，使得PAi+PAi+1+PAi+2之和最小，因为△AiAi+1Ai+2凸多边形A1A2…An，故该点的存在性获证。

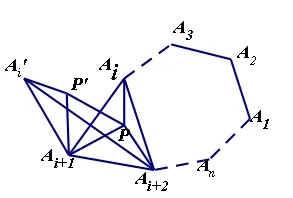
设点 是凸多边形 A1A2…An内一点，连接 PAi，PAi+1，PAi+2，把△PAiAi+1绕顶点Ai+1逆时针旋转60°，则△P'Ai'Ai+1≌△PAiAi+1，连接，则△PP'Ai+1为等边三角形。故 P'Ai＝ PAi，Ai'Ai+1＝ AiAi+1，PAi+1＝PP'

由此可得：（PAi+PAi+1+PAi+2）min=（P'Ai'+PP'+PAi+2）min=（Ai'Ai+2）

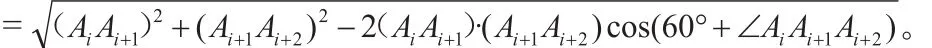
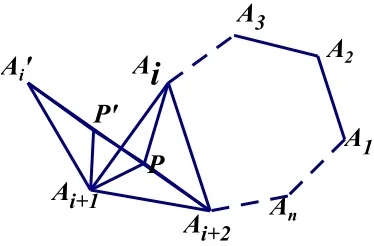
此时P点在线段Ai'Ai+2上，易知异于P点的任何点不产生最小值。

推论：当AiAi+1=Ai+1Ai+2时，

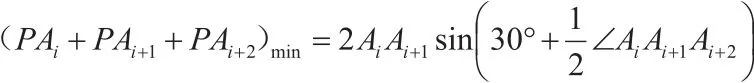
定理2：顺次连接正四、五边形内的费尔马点得到的正四、五边形分别与原正四、五边形相似，且相似比分别为

由（2）式知：点P1是 的平分线AP1与 的交点，由对称性类似地可得P2P3P4，易知四边形P1P2P3P4为正方形且与四边形 相似。

在△AP1B中由正弦定理知：

定义2：把顺次连接正多边形内的费尔马点形成的正多边形称之为“费尔马正多边形”。

证明：用Si表示第i个费尔马正方形的面积，由定理2知这些所有的费尔马正方形的面积构成一个公比为的无穷递缩等比数列。