数形结合方法的解题探究与教学实践

李立松

[摘  要] 数形结合思想将数学中的“数”与“形”有机地结合在一起，对于知识的理解和问题的解答十分有利. 初中阶段正是学生掌握数形结合思想方法的关键时期，对于该方法的教学不仅应渗透于具体的概念定理中，还应该结合具体的考题使学生掌握该方法的使用策略和精髓. 文章将分析数形结合方法在教学中存在的问题，并结合具体考题进行剖析，开展教学微设计，与读者交流学习.

[关键词] 二次函数;数形结合;教学;思考;实践

问题的提出

在九年级“二次函数”的章节教学中，需要让学生掌握二次函数的表达式，并能根据表达式绘制对应的函数图像，掌握函数的图像特点和对应的性质，其中隐含了数形结合的思想方法，即根据代数式联想函数的图像，根据图像的特点助力表达式的分析，从而实现二次函数的数与形的多角度研究. 同时该思想方法也是突破中考二次函数压轴题的重要解题方法，对透视考题结构，挖掘考题隐含条件，构建解题思路起着十分重要的作用. 但仅仅依靠教材概念讲解难以使学生充分掌握数形结合方法解题的具体策略，因此十分有必要结合考题使学生明晰方法的思想核心和内涵.

考题的例析

数形结合方法作为突破函数问题的重要方法，表面上是“数”与“形”相互结合来分析问题，但细致剖析其核心内容可概括为两点：一是以“数”思“形”，即根据函数表达式联想具体的函数图像;二是以“形”助“数”，即利用函数直观图像来分析表达式，确定问题的破解思路. 实际用于解题时就可以根据这两点进行研究，首先根据题干关于函数图像的信息绘制二次函数的图像，然后通过函数图像的特点来确定函数的性质，进而突破考题，以下面这道二次函数考题为例.

考题  在直角坐标系xOy中，抛物线L的解析式为y1=ax2+bx+c（a≠0），L与坐标系的x轴相交于点A（x1，0），B（x2，0），与y轴相交于点C，且O和C两点之间的距离为3，x1·x2<0，x1+x2=4，而点A和C位于直线y2=-3x+t上.

（1）试求点C的坐标;

（2）若y1随着自变量x的增大而增大，试求x的取值范围;

（3）现将抛物线y1向左平移n（n>0）个单位，记平移后y随着x的增大而增大的部分为P，再将直线y2向下平移n（n>0）个单位，若平移后直线与P存在公共点，试求2n2-5n的最小值.

突破解析：

（1）第一问求点C的坐标，题干中有两个条件，一是点C是抛物线与y轴的交点，二是“O和C两点之间的距离为3”，即OC=3，则OC=3或-3. 以“数”思“形”，可以此为条件绘制图1所示的图像，则可以确定抛物线有两种情形：开口向上或开口向下;以“形”助“数”，可确定点C的坐标为（0，3）或（0，-3）.

（2）研究x的取值范围，同样可以采用以“数”思“形”到以“形”助“数”的策略，即首先结合C的分类情况确定抛物线的表达式，然后根据表达式绘制对应的函数图像，最后根据图像的单调性确定x的取值范围. 考虑点C的坐标，分如下两种情形进行讨论：

①当点C的坐标为（0，3）时，点A和C均位于直线y2=-3x+t上，分别代入可得0=-3x1+t，

3=t，解得x1=1，

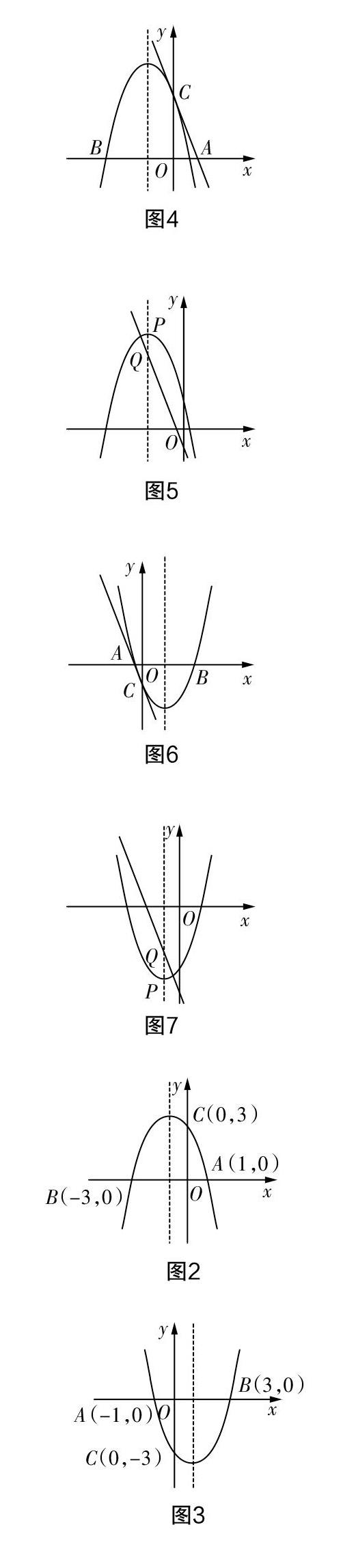
t=3，则点A（1，0）. 结合条件“x1·x2<0，x1+x2=4”可得x2= -3，进一步可确定点B（-3，0），从而可确定抛物线的解析式为y1=a（x-1）（x+3），最后将点C的坐标代入上式，可以确定抛物线的表达式y1=-x2-2x+3，可计算出对称轴为x=-1. 根据其表达式可以绘制如图2所示的图像，图像开口向下. 由图像可知：当x<-1时，y1随着自变量x的增大而增大，故x的取值范围为x<-1.

②当点C的坐标为（0，-3）时，同理可确定抛物线的表达式y1=x2-2x-3，圖像的对称轴为x=1，根据其表达式可以绘制如图3所示的图像，图像开口向上. 由图像可知：当x>1时，y1随着自变量x的增大而增大，故x的取值范围为x>1.

综合上述情形的①和②，可知：当点C为（0，3）时，抛物线表达式的a=-1，x<-1;当点C为（0，-3）时，抛物线表达式的a=1，x>1.

（3）对于该问同样需要考虑点C的坐标，通过分类讨论确定抛物线的图像，借助图像确定最值.

①当点C为（0，3）时，a=-1，则y1= -（x+1）2+4，y2=-3x+3，y1向左平移n个单位，可得y3=-（x+1+n）2+4，y2向下平移n个单位，可得y4=-3x+3-n. 在图4中分别绘制y1和y2的图像，然后在图5中绘制平移后的图像，则区域P就是抛物线对称轴左侧的部分，要使直线与区域P存在公共点，则需满足抛物线顶点P位于点Q之上，即x=1-n时，y3≥y4，代入可解得n≥1.

②当点C为（0，-3）时，a=1，则y1=（x-1）2-4，y2=-3x-3，对应可得平移后的表达式为y3=-（x-1+n）2-4，y4=-3x-3-n. 同样绘制平移前后的图像，如图6和图7，同理可确定区域P（对称轴右侧），存在公共点的条件为抛物线顶点P位于点Q的下方，即x=1-n时，y3≤y4，代入可解得n≤-1. 考虑到n>0，将其舍去.

综上可知，n≥1，2n2-5n=2n-2-，定义域为n≥1，则n=时2n2-5n可取得最小值-.

在考题教学中可以进行对应的微设计，逐步引导学生掌握数形结合的解题策略，以上述考题的第（1）、（2）问为例：

1. 教学环节一：呈现题干，基础分析

已知抛物线L：y1=ax2+bx+c（a≠0），与x轴的交点为A（x1，0），B（x2，0），与y轴的交点为C，若点C到点O的距离为3，试求点C的坐标.

引导：利用代数式表示“点C到点O的距离为3”.

2. 教学环节二：深入研究，探究解析式

题干信息同上，若x1·x2<0，x1+x2=4，点A和C位于直线y2=-3x+t上，试求二次函数的解析式.

引导：①利用上述点C的坐标，结合条件“A和C位于直线y2=-3x+t上”求对应点A的坐标.

②结合条件“x1·x2<0，x1+x2=4”确定对应点B的坐标.

③利用点A，B，C的坐标求解抛物线的解析式.

3. 教学环节三：以“数”思“形”，构建函数图像

利用上述抛物线的解析式，结合关键点绘制抛物线的图像.

引导：根据抛物线的解析式，确定函数的对称轴，然后分别标出图像的顶点、与x轴的交点和对称轴，进而绘制图像.

4. 教学环节四：以“形”助“数”，研究取值问题

在上述条件成立的情况下，如果 y1随着自变量x的增大而增大，则x的取值范围为多少？

引导：根据具体的抛物线图像进行研究，y1随着自变量x的增大而增大，则表示需要取图像上的单调递增区间，根据函数的递增区段来分析对应的自变量取值.

教学的思考

1. 立足考题教学，探寻着力点

数形结合思想是初中数学最为重要的思想方法之一，许多教师在教学中仅在函数的性质教学中进行了简单的渗透，偏重于利用数形结合思想使学生理解具体的概念，但数形结合同样是一种重要的解题方法和策略，掌握数形结合的方法对于提高学生的解题效率是十分有利的. 因此应该从方法的“概念教学”走向方法的“解题教学”，即结合具体的考题，通过对考题的细致剖析使学生充分体会数形结合思想的应用内涵，形成数形结合分析问题的意识. 将考题作为方法学习的着力点，不仅是提升学生综合解题能力的应用要求，同時也是当下素质教育的发展要求，将概念与应用相结合可以使学生深刻体会方法的精髓所在.

2. 微设教学环节，体会应用思想

数形结合方法应用解题包含有两层深义，一是以“数”思“形”，通过适度的运算来获得关键的数据，结合数据来构建图像;二是以“形”助“数”，充分利用图像的直观性，明确图像结构，透视考题本质，探寻问题解答的途径，即利用图像的性质来探究数学规律，使复杂的代数问题转化为与图像性质相关的问题. 考虑到学生的理解能力，为使学生充分掌握该方法的解题策略，进行考题教学时要合理的采用教学微设计的方式，将复杂的综合问题拆分为多个简单的问题，然后通过对几个分问题的引导使学生掌握数形结合分析问题的具体步骤. 如上述考题的微设计，首先利用分问题引导学生进行数据分析，利用数据来绘制函数图像，然后利用图像来简捷地求解问题，这样的方式不仅有利于学生理解方法的应用性，还可以培养学生的逻辑思维.