杨辉三角中的“几何图形”
■陕西省武功县教育局教研室 李 歆
杨辉,是我国南宋时期一位杰出的数学家。在他所著的《详解九章算法》一书中,画了一张表示二项式展开后的系数构成的三角图形,现在简称为“杨辉三角”,它是数学史上的一大重要研究成果。
一般地,杨辉三角是指如下的图形:

图1
从上面的图形中,很容易发现,这个三角形的两条斜边都是由数字1组成的,而其余的数都等于它肩上的两个数相加。例如,2=1+1,3=1+2,4=1+3,6=3+3,等等。在一般情形下,若令=0,则有(r=1,2,…,n),这个等式被称为杨辉恒等式,它是杨辉三角最基本的性质。
当我们把杨辉三角中的上下左右相连的部分数看成一个独立的整体,那么就会发现一些非常有趣的“几何图形”,从而挖掘出杨辉三角“形”的秘密。
一、杨辉三角中的“三角形”
例1在图2所示的“三角形”中,第7行最中间的数是__。

图2
解:因为C=1,C=3,C=10,所以此“三角形”中第1行、第3行、第5行最中间的数依次应是杨辉三角中的第2行第1个数、第4行第2个数、第6行第3个数,由此可知,此“三角形”中的第7行最中间的数应是杨辉三角中的第8行第4个数,即为C=
点评:求解此题关键有两点:一是找出第7行是杨辉三角中的第几行,二是找出最中间的数是杨辉三角中的第几行的第几个数。只有找出这两个结果,才能顺利解题。
二、杨辉三角中的“梯形”
例2在图3所示的“梯形”中,第8行的第2个数是__。
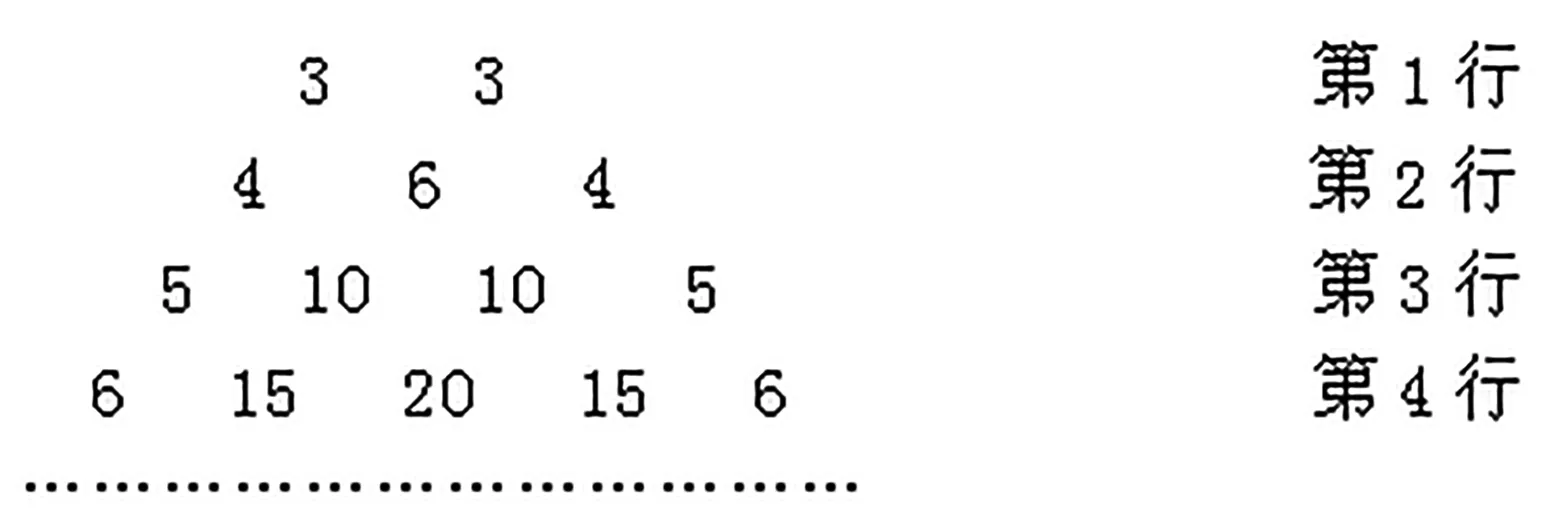
图3
解:因为C=3,所以此“梯形”中第1行的第2个数应是杨辉三角中的第1+3=4行的第3个数,由此可知,此“梯形”中的第8行的第2个数应是杨辉三角中的第8+3=11行的第3个数,即为
点评:由此“梯形”中第1行的第2个数入手,找出它在杨辉三角中的具体位置,是求解此题的关键。
三、杨辉三角中的“平行四边形”
例3在图4所示的“平行四边形”中,第6行的第1个数是__。

图4
解:因为C=4,C=10,C=20,C=35,所以此“平行四边形”中的前四行的第1个数依次应是杨辉三角中的第5行的第2个数、第6行的第3个数、第7行的第4个数、第8行的第5个数,由此可知,此“平行四边形”中的第6行的第1个数应是杨辉三角中的第10行的第7个数,即
点评:如果从第2行起,移动每一个数,并将它们与第1行的各个数对齐,那么此“平行四边形”就变成了“矩形”,这样一变,图中的规律便变得隐蔽起来,从而题目的难度将会增加。
四、杨辉三角中的“菱形”
例4在图5所示的菱形中,第(5)个“菱形”是__。

图5
解:由前4个“菱形”可知,第(5)个“菱形”最上面的数应为5,第2行的两个数应为15,6,最下面的数应为15+6=21。
点评:此题给出的前4个“菱形”,具有明显的规律性:(1)每个“菱形”的第1行是按顺序排列的自然数;(2)每个“菱形”右上斜边是连续的两个数;(3)从第2个“菱形”开始,后面每1个“菱形”第2行的第1个数是前1个“菱形”最下面的数。
五、杨辉三角中的“六边形”
例5在图6所示的“六边形”中,第(4)个“六边形”是__。

图6
解:由前3个“六边形”可知,第4个“六边形”第1行的两个数应为35,35,在杨辉三角中找出这两个数的位置以及下面两行相邻的数,即得此“六边形”中第(4)个“六边形”是:
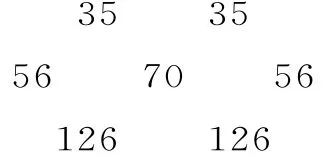
点评:按照题中给出的前3个“六边形”,写出第(4)个“六边形”的第1行很容易,关键是如何找出第2行的第1个(或第3个)数。对此可以利用“还原法”和“补数法”完成,即将题中给出的3个“六边形”先还原为杨辉三角,然后补上所需要的数,即可得到答案。
六、“倒立”的杨辉三角
例6图7是“倒立”的杨辉三角,则第(4)个“倒立”的杨辉三角最下面的数是__。

图7
解:由前3个图示可知,第4个“倒立”的杨辉三角的第1行的五个数应为1,4,6,4,1,由此可知第2行的四个数应为5,10,10,5,第3行的三个数应为15,20,15,第4行的两个数应为35,35,第5行的一个数应为70,所以第(4)个“倒立”的杨辉三角最下面的数是70。
点评:如果由前3个图示给出的最下面的数2,6,20,去猜测或者求解第(4)个“倒立”的杨辉三角中最下面的数,那么难度会很大,但是由上而下去看,则规律明显,虽然要一行一行去推出每个数,却能稳操胜券。
七、“侧放”的杨辉三角
例7图8是“侧放”的杨辉三角,则第(4)个“侧放”的杨辉三角最前面的数是__。
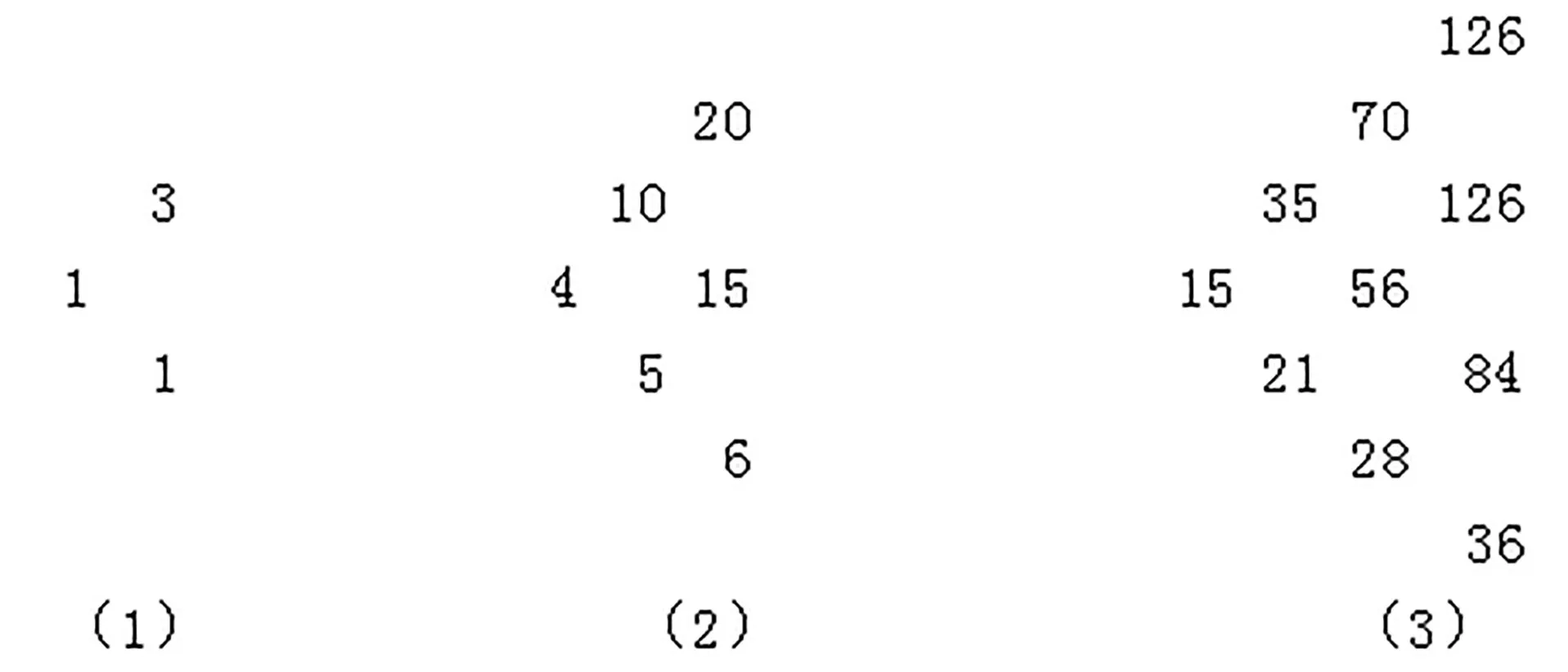
图8
解:由给出的图示可知,第1个、第2个、第3个“侧放”的杨辉三角最前面的数依次是1,4,15,因为C=1,C=4,C=15,所以它们应是杨辉三角第3行的第1个数、第5行的第2个数、第7行的第3个数,由此可知,第(4)个“侧放”的杨辉三角最前面的数应是杨辉三角第9行的第4个数,即为C=
点评:一般地,按照此题“侧放”的杨辉三角,第(n)个最前面的数是
八、“X型”的杨辉三角
例8图9是“X型”的杨辉三角,则第(4)个“X型”的杨辉三角最中间的数是__。

图9
解:由给出的图示可知,第(1)个、第(2)个、第(3)个“X型”的杨辉三角最中间的数依次是3,10,35,因为C=3,C=10,C=35,所以它们应是杨辉三角第4行的第2个数、第6行的第3个数、第8行的第4个数,由此可知,第(4)个“X型”的杨辉三角最中间的数应是杨辉三角中第10行的第5个数,即为C
点评:“X型”的杨辉三角,可以看成是由一个杨辉三角中的“三角形”与另一个“倒立”的杨辉三角合并得到的,因此,此题可以分解为下列两个子问题。
变式1:在图10所示的“三角形”中,第(4)个“三角形”最上面的数是__。

图10
变式2:图11是“倒立”的杨辉三角,则第(4)个“倒立”的杨辉三角最下面的数是__。

图11
杨辉三角是我国古代数学传承下来的珍贵文化,它形中有数,数中有形,看似简单平凡,却内涵十分丰富,是数与形结合的最佳产物。当我们走进杨辉三角,对它的内部结构和形状进一步探究时,就会挖掘出许多有价值的智力资源,从而不断提升我们的解题智慧。

