杨辉三角的探究之旅
高莹


一、杨辉三角之由来
杨辉三角是一个特殊的数阵,最早出现在北宋贾宪的“开方作法本源图”中。南宋时期,杨辉在其著作《详解九章算术》中予以引用,且注明了“出释锁算书,贾宪用此术”。元朝时期,朱世杰对杨辉三角作了进一步研究和推导,得出了高阶差分数列的求和。
据说在1636年,法国帕斯卡在13岁时发现了这个三角形,这个表在欧洲被认为是帕斯卡首先发现的,因此也被称作“帕斯卡三角”。但此时已经距我国杨辉三角的发现过了六百年左右,这足以说明我国古代数学的卓越成就,在世界数学史占有重要地位。因此有些书上称之为“中国三角形”(Chinese triangle)。
杨辉三角在整个数学史中的应用非常广泛,北宋的贾宪用其手算高次方根,元朝的朱世杰用其研究高阶差分数列(垛积术),牛顿用其算微积分,华罗庚拓宽思路,还谈到了差分方程,无穷级数等。同学们,今天就让我们穿越时光隧道,沿着大师的足迹,来一次杨辉三角的探究之旅!
二、初探杨辉三角
探究角度一:杨辉三角与二项式系数
问题1:通过二项式定理的学习,请同学们观察当n依次取1,2,3…时,(a+b)n展开式的二项式系数,即如图2所示的二项式系数表,以及杨辉三角如图1,请大家说说它们之间的联系?
生:杨辉三角的第n行就是(a+b)n的二项式系数。
问题2:结合杨辉三角(图1)以及二项式系数表,找一找二项式系数有着怎样的规律?二项式系数又有哪些性质?
生3:我发现每一行大小的变化都是有规律的,当n为偶数时,中间的一项最大,当n为奇数时,中间的两项最大③。
生4:每一行的和为一个有规律的数,1,2,4,8…,即C0n+C1n+…+Cnn=2n④。
师:很好,大家结合杨辉三角发现了二项式系数的规律和性质,其实啊,杨辉三角不仅与二项式系数有种种联系,它还与我们生活中的一种有趣的现象相联系,讓我们借助杨辉三角来进行分析。
拓展1:如图3的弹子游戏,小球(黑色)向容器内跌落,碰到第一层阻挡物后等可能地向两侧跌落,碰到第二层阻挡物等可能地向两侧第三层跌落,如此,一直下跌,小球最终落入最底层,根据落入区域获取奖品。试问:为什么中间区奖品低于两边区奖品?
拓展2:除了与生活相关外,还与数学本身有联系,下面我们利用③和集合联系起来:恰好可以解释必修一学习的{a1,a2…an}中子集的个数为什么是2n。
拓展3:继续联系我们学习的知识,“纵横路线图”是学习组合时接触的一类问题:若某地区的部分街道图是纵横各有四条路,如果从A处走到B处(只能由北到南,由西向东),请问有多少种不同的走法?将纵横路线图旋转如图4的杨辉三角图,对应的结果一目了然就
是C48。
师:可见杨辉三角不仅仅和二项式系数有关系,还对我们解决一些生活问题,以及其他数学问题都有很大的帮助,感觉用杨辉三角一解释就变得容易了,这也是杨辉三角的魅力所在,那么它还有什么奥秘呢?我们继续探究。
三、再探杨辉三角
探究角度二:杨辉三角与数列
问题3:换一个角度观察杨辉三角,将杨辉三角摆成直角三角形,观察由这些数字构成的数列,你能否发现其中的规律?
结论1.数列求和有规律:
即:在第r+1条斜线上(从右上到左下)前n-r个数字的和,等于第r+2条斜线上的第n-r个数。
拓展4:其中结论1同时还在生活当中应用普遍:
“堆垛术”中常见的三角堆垛,生活中在食品橱窗中看到的将食品罐堆放成如下的形式:底层是每边为n的三角形,依次往上堆边长少1的三角形,求食品罐的总数。(这就是结论1中r=4的模型)是不是特别简单?
问题4:从另一斜着的角度观察数字,例如第一斜线的数字是1,第二斜线的数字是1,第三斜线的数字是1,1,第四斜线的数字是1,2,第五斜线的数字是1,3,1,第六斜线的数字是1,4,3,…求出这些数字的和,并仔细观察,你能发现什么规律?
1,1,2,3,5,8,13,21,34…
结论2.此数列满足:a1=1,a2=1,an=an-1+an-2(n≥3,n∈N)
拓展5:这就是著名的斐波那契数列。
中世纪意大利数学家斐波那契的《算术之法》中提出了一个很有趣的问题:假定一对刚出生的小兔子一个月就能长成大兔子,过一个月生下一对小兔子,且之后每个月都生一对小兔子。设所生一对兔子均为一雄一雌,且均存活。问一对刚出生的小兔一年内可以繁殖成多少对兔子?
关于兔子繁殖问题从杨辉三角可以得到答案:斜线上各行数字的和1,1,2,3,5,8,13,21,34…,正好是第一个月后的兔子,第二个月后的兔子,第三个月后的兔子,……,第n个月后的兔子的对数。答案就是上述数列的第13个数,即233。这个数列称之为斐波那契数列。它所具有的性质都是杨辉三角中所蕴含的性质。
四、三探杨辉三角
探究角度三:杨辉三角的“形”
问题5:请同学们将图中杨辉三角的偶数、奇数分别标出,会有什么发现?
发现1:所有偶数都呈倒立的正三角形状排列,奇数都呈正立的正三角形形状排列;
发现2:边长特点:3,7,15,31,63,…规律:3=22-1,7=23-1,15=24-1,31=25-1,即所有偶数依次排出以2n-1(n∈N*)的长度为边长的倒立正三角形。
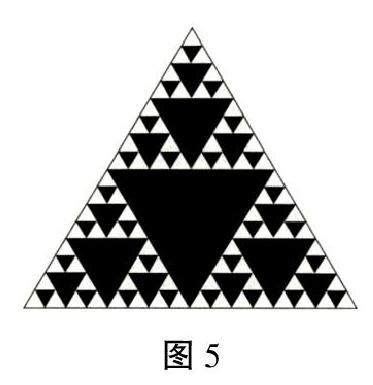
拓展6:把这些倒立正三角形从杨辉三角中挖去,剩余部分就是有趣的西尔平斯基衬垫.
如图5.(由波兰数学家西尔平斯基于1951年发现,故而得名)
这体现了杨辉三角的“形”的结构特点,也体现了数学的简洁美和抽象美。
五、小结与收获
探究杨辉三角的“数”与“形”:
西尔平斯基衬垫体现了杨辉三角的“形”的结构特点,而“形”决定于杨辉三角“数”的构成,是杨辉三角的本质的反映,杨辉三角“数”与“形”的结合如此完美令人叹为观止。杨辉三角与组合数、数列、数学归纳法联系在一起,合乎情理,一气呵成,体现了数学的和谐之美,同时,杨辉三角又能与著名的斐波那契数列、有趣的西尔平斯基衬垫联系在一起,使人感受到数学学习的奥妙无穷,体现了数学的奇异美。杨辉三角还是对一些数学规律的高度概括和抽象,所以说数学即是蕴含“真”科学,又是蕴含“美”科学,可谓是“真美”。
编辑 李烨艳

