全国名校计数原理综合测试题答案与提示

一、选择题

1.C

2.A

3.B

4.C 提示：第一步,安排A有2种方法;第二步,在剩余的5个位置选取相邻的两个排B,C,有4种排法,而B,C位置互换有2种方法;第三步,安排剩余的3个程序,有种排法。共有=96(种)排法。

5.D 提示：512012+a=(13×4-1)2012+a,被13整除余1+a,结合选项可得a=12时,512012+a能被13整除。

7.C

10.B 提示：从这9名大学生志愿者中任选3名派到3所学校支教,则有A种选派方案,3名志愿者全是男生或全是女生的选派方案有A+A种,故符合条件的选派方案有A-(A+A)=420(种)。

11.A 提示：先涂三棱锥P-ABC的三个侧面,然后涂三棱柱的三个侧面,共有C×C×C×C=3×2×1×2=12(种)不同的涂法。

12.D 提示：从P点处进入结点O以后,游览每一个景点所走环形路线都有2个入口或2个出口,若先游览完A景点,再进入另外两个景点,最后从Q点处出有(4+4)×2=16(种)不同的方法。同理,若先游览B景点,有16种不同的方法;若先游览C景点,有16种不同的方法。因此,所求的不同游览线路有3×16=48(种)。

13.D

14.B 提示：先从除甲、乙外的4人中选取1人去巴黎,再从其余5人中选3人去伦敦、悉尼、莫斯科,共有不同选择方案A·A=240(种)。

15.D

16.B

17.D

18.C 提示：利用二项展开式的通项公式求解,由题意知,C=C,故n=9。

二、填空题

19.80

20.16

21.24

22.1 或-3 提示：令x=0,得到a0+a1+a2+…+a9=(2+m)9。令x=-2,得到a0-a1+a2-a3+…-a9=m9。

所以(2+m)9m9=39,即m2+2m=3。

解得m=1或-3。

三、解答题

23.“完成这件事”需选出男、女队员各1人,可分两步进行：

第一步,选1名男队员,有5种选法;

第二步,选1名女队员,有4种选法。

所以共有5×4=20(种)选法。

24.按照焊接点脱落的个数进行分类：

第1类,脱落1个,有1,4,共2种情况;

第2类,脱落2个,有(1,4),(2,3),(1,2),(1,3),(4,2),(4,3),共6种情况;

第3类,脱落3个,有(1,2,3),(1,2,4),(2,3,4),(1,3,4),共4种情况;

第4类,脱落4个,有(1,2,3,4),共1种情况。

根据分类加法计数原理,共有2+6+4+1=13(种)焊接点脱落的情况。

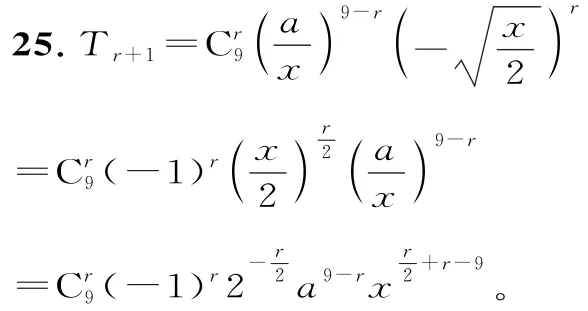
(1)令x=1,得各项系数的和为(1-2)8=1。

27.由题意知,按选择投资城市的个数分两类：

②投资2个城市,其中1个城市投资1个项目,另1个城市投资2个项目,即先从3个项目中选2个看作1个元素(投资在某1个城市),另1个项目看作1个元素(投资在另1个城市),然后把这2个元素在4个城市里进行选排,这样有CA种方案。

28.(1)为保证“恰有1个盒不放球”,先从4个盒子中任意取出去1个,问题转化为“4个球,3个盒子,每个盒子都要放球,共有几种放法?”,即把4个球分成2,1,1的三组,然后再从3个盒子中选1个放2个球,其余2个球放在另外2个盒子内,由分步乘法计数原理知,共有CCC×A=144(种)放法。

(2)“恰有1个盒内有2个球”,即另外3个盒子放2个球,每个盒子至多放1个球,也即另外3个盒子中恰有1个空盒,因此,“恰有1个盒内有2个球”与“恰有1个盒不放球”是同一件事,所以共有144种放法。