一种三角换元的代数形式及其应用

■江西省丰城中学 吴爱龙 聂燕凤

在一定条件下,求二元函数的最值问题时,常遇到形如a+b=1,a＞0,b＞0之类的约束条件,联想到三角中的同角三角函数的基本关系式sin2θ+cos2θ=1,可令a=cos2θ,于是有但由于其中涉及新教材中早已删了的同角三角函数的其他三角关系secθ·cosθ=1,cscθ·sinθ=1,1+tan2θ=sec2θ,1+cot2θ=csc2θ,又注意到tanθ·cotθ=1,于是我们可以将上述变换改进为代数形式：令,其中x＞0,y＞0,且xy=1,这样应用起来就没有超纲之嫌了。

下面列举数例说明其应用。

1.直接作出代换

例1(2018届镇江高三卷)已知a,b为正数,且,则的最小值为__。

解析：令,其中x＞0,y＞0,且xy=1,则a=1+x,b=1+y。

所以：

例2(2019届无锡高三期中)设x,y为正实数,且=1,则xy的最小值为__。

解析：令其中a＞0,b＞0,且ab=1。

于是x=4a+3,y=3b+1。

例3(2019届徐州高三期中)已知正实数a,b,并且满足a+2b=1,则的最小值为__。

解析：令,其中x＞0,y＞0,且xy=1。于是：

点评：此类题型题设条件很明显,较易联想,作出变换,运用二元均值不等式便可迅速得出答案。

2.稍变形,再代换

例4(2016年广东省高中联赛预赛)若正数x,y满足x+3y=5xy,则3x+4y的最小值为__。

解析：由题设知,其中a＞0,b＞0,且ab=1,则

例5(2017年苏州、无锡、常州、镇江二模)已知a,b均为正数,且ab-a-2b=0,则的最小值为__。

解析：因为ab-a-2b=0,所以=1。令,其中x＞0,y＞0,且xy=1,则于是：

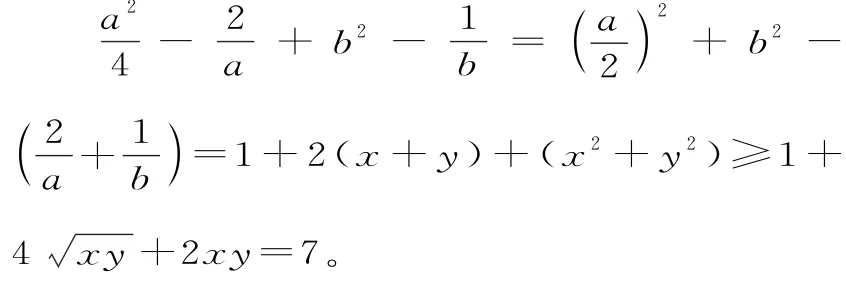
点评：此类题型只要对题设条件稍作变形,亦可快速作出代换,准确得出答案。

3.巧变形,妙代换

例6(2019届镇江高三期中)已知x的最小值为__。

解析：由题设知,其中a＞0,b＞0,且ab=1。于是：

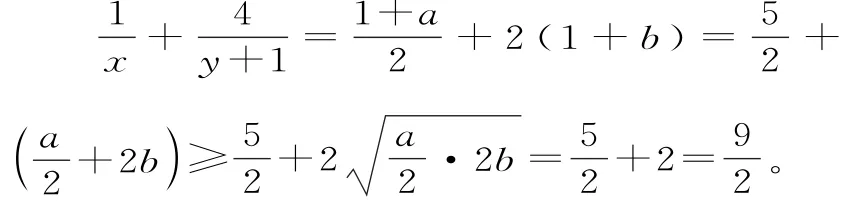
例7(2019届扬州高三期中)已知正实数a,b满足2a+b=3,则的最小值是__。

解析：整理得又由题设知2a+(b+2)=5,即,其中x＞0,y＞0,且xy=1,则

例8(第26届“希望杯”)若正数a,b满足2a+b=1,则的最小值是__。

解析：由题设知令,其中x＞0,y＞0,且xy=1,则

点评：此类题型题设条件看似简单,但必须结合目标函数,先适当变形,再作出巧妙代换,解法灵活,难度稍大。

4.先化归,后代换

例9已知函数,若f(x1)+f(2x2)=1,则f(x1+2x2)的最小值为( )。

解析：将原函数变形为f(x)=1-因为f(x)+f(2x)=1,所以12

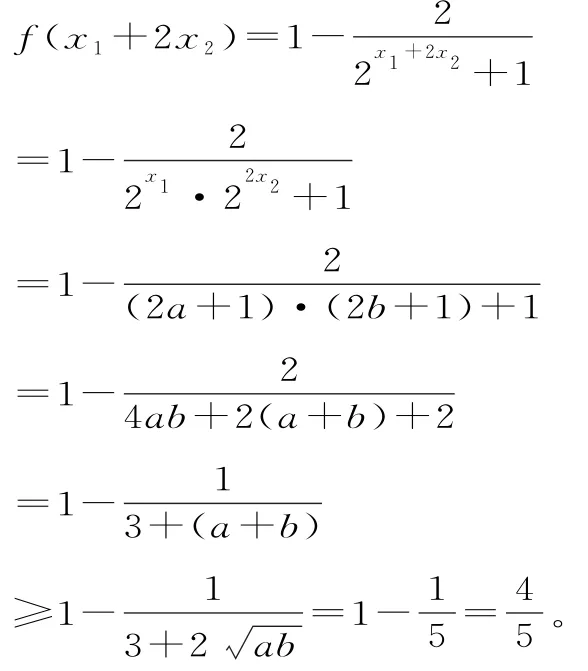
当且仅当a=b=1,即x1=log23,x2=时,f(x1+2x2)的最小值为,选B。

点评：这是一个以指数函数为背景的二元函数最值问题,必须将其转化为文中所述类型后再作出代换解之。

必须指出,二元函数条件最值问题大都还有别的解法,但通过上述诸例可以看出,该种变换往往能将复杂的目标函数化得较为简单,甚至能揣摩出目标函数的构建或设计过程,所以解法也就自然显得更为简捷或重要了。