涂色问题的常见解法及策略
■江苏省盐城市时杨中学 刘长柏
对于涂色问题的解法,拨云破雾、还其本来面目,就会发现实质是用分类或分步计数原理导航,通过深入缜密分析题意,将原题化归为熟悉的排列、组合或综合题型,逐类分步推理求解的。涂色问题的常见解法:根据分步计数原理,对各个区域分步涂色;根据共用了多少颜色分类讨论;根据不相邻区域是否同色分类讨论等。
一、根据分步计数原理,对各个区域分步涂色
例1用红黄绿三种颜色给图1中的5个带状格子涂色。要求每格涂一种颜色且相邻格子不能涂同一种颜色,共有多少种不同的涂法?

图1
分析:根据分步计数原理,对各个区域分步涂色,这是处理染色问题的基本方法。
解:从满足一格一颜色、邻格不同色的限制条件入手,分成三类:
练习1:用5种不同的颜色给图2中标①、②、③、④的各部分涂色,每部分只涂一种颜色,相邻部分涂不同颜色,则不同的涂色方法有多少种?

图2
解:先给①号区域涂色有5种方法,再给②号涂色有4种方法,接着给③号涂色方法有3种,由于④号与①、②不相邻,因此④号有4种涂法,根据分步计数原理,不同的涂色方法有5×4×3×4=240(种)。
二、根据共用了多少颜色分类讨论
例2如图3所示,花坛内有5个花池,有5种不同颜色的花卉可供栽种,每个花池内只能栽种同颜色的花卉,相邻两池的花卉颜色不同,则最多有多少种栽种方案?
分析:本题要完成的事件是花池内栽种花卉;由于5种不同颜色的花卉可供选择,所以可选择3种、4种、5种不同颜色的花卉栽种,可见有3类方法可独立完成这件事,而每一类又不能“一次性”完成,所以分步进行。
解:由题意知,最少用三种颜色的花卉,按照花卉选种的颜色可分为三种方案,即用三种颜色、四种颜色、五种颜色。
①当用三种颜色时,花池2、4栽同种颜色的花卉,有5种方案,花池3、5栽同种颜色的花卉,有4种方案,花池1有3种栽种方案,由分步计数原理知5×4×3=60(种)方案。
②当用四种颜色时,则花池2、4栽同种颜色的花卉或花池3、5栽同种颜色的花卉。若花池2、4栽同种颜色的花卉,则花池2、4有5种方案,花池3有4种栽种方案,花池5有3种栽种方案,花池1有2种栽种方案,由分步计数原理得5×4×3×2=120(种)栽种方案;若花池3、5栽同种颜色的花卉,同理得有5×4×3×2=120(种)栽种方案;再由分类计数原理得共有120+120=240(种)栽种方案。

图3
③当用五种颜色时,花池1有5种栽种方案,花池2有4种栽种方案,花池3有3种栽种方案,花池4有2种栽种方案,花池5有1种栽种方案,由分步计数原理得5×4×3×2×1=120(种)栽种方案。
根据分类计数原理得60+240+120=420(种)栽种方案。
点评:对于一些较复杂的题目,往往既要分类又要分步,也就是说既要应用分类加法计数原理又要运用分步乘法计数原理,在计数时应让两个原理协同作用。当两个原理混合使用时,一般是先分类再分步,在每类中再分步。
练习2:将一个四棱锥S-ABCD的每个顶点染上一种颜色,并使同一条棱的两端点异色,如果只有5种颜色可供使用,那么不同的染色方法的总数是多少?
解:满足题设条件的染色至少要用三种颜色。
(1)若恰用三种颜色,可先从五种颜色中任选一种染顶点S,再从余下的四种颜色中任选两种涂A、B、C、D四点,此时只能A与C、B与D分别同色,故有CA=60(种)方法。
(2)若恰用四种颜色染色,可以先从五种颜色中任选一种颜色染顶点S,再从余下的四种颜色中任选两种染A与B,由于A、B颜色可以交换,故有A种染法;再从余下的两种颜色中任选一种染D或C,而D与C中另一个只需染与其相对顶点同色即可,故有CACC=240(种)方法。
综上所知,满足题意的染色方法数为60+240+120=420(种)。
三、根据不相邻区域是否同色分类讨论
例3用红、黃、蓝、白四种颜色涂矩形ABCD的四条边,每条边只涂一种颜色,且使相邻两边涂不同的颜色,如果颜色可以反复使用,共有多少种不同的涂色方法?
分析:涂色按AB→BC→CD→DA的顺序进行,对AB、BC涂色有4×3=12种涂色方法。由于CD的颜色可能与AB同色或不同色,这影响到DA颜色的选取方法数,故分类讨论。
解:当CD与AB同色时,这时CD对颜色的选取方法唯一,则DA有3种颜色可供选择;当CD与AB不同色时,CD有两种可供选择的颜色,DA也有两种可供选择的颜色。从而对CD、DA涂色有1×3+2×2=7(种)涂色方法。
由乘法原理得,总的涂色方法数为12×7=84(种)。
点评:根据某两个不相邻区域是否同色分类讨论,从某两个不相邻区域同色与不同色入手,分别计算出两种情形的种数,再用加法原理求出不同涂色方法总数。
四、涂色问题中的转化
例4已知四棱锥P-ABCD,如图4,用4种不同的颜色涂在四棱锥的各个面上,要求相邻不同色,有多少种涂法?

图4

图5
分析:如图5,区域1、2、3、4相当于四个侧面,区域5相当于底面,进而根据共用颜色多少种分类讨论。
解:如图5,区域1、2、3、4相当于四个侧面,区域5相当于底面。根据共用颜色多少种分类:
(1)最少要用3种颜色,即1与3同色、2与4同色,此时有A种方法;
(2)当用4种颜色时,1与3、2与4两组中只能有一组同色,此时有CA种涂法。
点评:这种面的涂色问题可转化为区域涂色问题,再利用区域的涂色方法进行求解。
练习3:直线x=m,y=x将圆面x2+y2≤4分成若干块,现用5种颜色给这若干块涂色,每块只涂一种颜色,且任意两块不同色,共有120种涂法,则m的取值范围是( )。
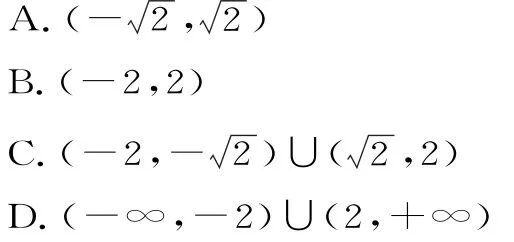

图6
解:如图6,①当m≤-2或m≥2时,圆面x2+y2≤4被分成2块,涂色方法有20种;②当<2时,圆面x2+y2≤4被分成3块,涂色方法有60种;③当时,圆面x2+y2≤4被分成4块,涂色方法有120种。所以m的取值范围是,故选A。

