全国名校计数原理综合测试题
■山东省利津县第一中学 胡 彬
一、选择题
1.从集合{0,1,2,3,4,5,6}中任取2个互不相等的数a,b组成复数a+bi,其中虚数有( )。
A.30个 B.42个
C.36个 D.35个
2.数列{an}共有6项,其中4项为1,其余2项各不相同,则满足上述条件的数列{an}共有( )。
A.30个 B.31个
C.60个 D.61个
A.5 B.10 C.20 D.40
4.在航天员进行的一项太空实验中,先后要实施6个程序,其中程序A只能出现在第一步或最后一步,程序B和C实施时必须相邻,则实验顺序的编排方法共有( )。
A.24种 B.48种
C.96种 D.144种
5.设a∈Z,且0≤a<13,若512012+a能被13整除,则a=( )。
A.0 B.1 C.11 D.12
6.在数字1,2,3与符号“+”,“-”这5个元素的所有全排列中,任意2个数字都不相邻的全排列方法共有( )。
A.6种 B.12种
C.18种 D.24种
7.电视台在直播2008年北京奥运会时要连续插播5个广告,其中3个不同的商业广告和2个不同的奥运宣传广告,要求最后播放的是奥运宣传广告,且2个奥运宣传广告不能连播,则不同的播放方式有( )。
A.120种 B.48种
C.36种 D.18种
A.4 B.-4 C.26D.-26
9.航空母舰“辽宁号”将进行一次编队配置科学试验,要求2艘攻击型核潜艇一前一后,3艘驱逐舰和3艘护卫舰分列左右,每侧3艘,同侧不能都是同种舰艇,则舰艇分配方案的方法数为( )。
A.72 B.324
C.648 D.1296
10.某高校从5名男大学生志愿者和4名女大学生志愿者中选出3名志愿者派到3所学校支教(每所学校一名志愿者),要求这3名志愿者中男、女大学生都有,则不同的选派方案共有( )。
A.210种 B.420种
C.630种 D.840种
11.如图1所示,几何体是由一个正三棱锥P-ABC与正三棱柱ABCA1B1C1组合而成,现用3种不同颜色对这个几何体的表面染色(底面A1B1C1不涂色),要求相邻的面均不同色,则不同的染色方案共有( )种。

图1
A.12 B.18 C.24 D.42
12.一个旅游景区的游览线路如图2所示,某人从P点处进,Q点处出,游览A,B,C三个景点及沿途风景,则不重复(除交汇点O外)的不同游览线路有( )。
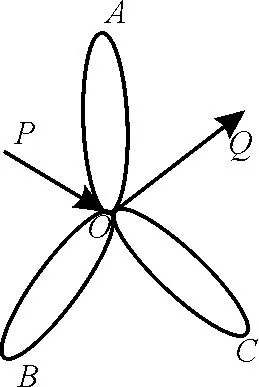
图2
A.6种 B.8种
C.12种 D.48种
13.5 个代表分4张同样的参观券,每人最多分一张,且全部分完,那么不同分法共有( )。
C.54种 D.C种
14.从6个人中选4人分别到巴黎、伦敦、悉尼、莫斯科4个城市游览,要求每个城市都有人游览,每人只游览一个城市,且这6人中甲、乙2人不去巴黎游览,则不同的选择方案共有( )。
A.300种 B.240种
C.144种 D.96种
15.若x∈(0,+∞),则(1+2x)15的二项展开式中系数最大的项为( )。
A.第8项 B.第9项
C.第8项和第9项 D.第11项
16.从甲、乙等5名志愿者中选出4名,分别从事A,B,C,D四项不同的工作,每人承担一项。若甲、乙2人均不能从事A工作,则不同的工作分配方案共有( )。
A.60种 B.72种
C.84种 D.96种
17.从20名男同学,10名女同学中任选3名参加体能测试,则选到的3名同学中既有男同学又有女同学的不同选法的种数为( )。
A.1260 B.4060
C.1140 D.2800
A.4284 B.4882
C.5376 D.6056
二、填空题
19.(1+2x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5,则a3=__。
20.某市政府召集5家企业的负责人开年终总结经验交流会,其中甲企业有2人到会,其余4家企业各有1人到会,会上推选3人发言,则这3人来自3家不同企业的可能情况的种数为__。
21.张、王两家夫妇各带1个小孩一起到动物园游玩,购票后排队依次入园。为安全起见,首尾一定要排2位爸爸,另外,2个小孩一定要排在一起,则这6人的入园顺序排法种数为__。(用数字作答)
22.若(x+2+m)9=a0+a1(x+1)+a2(x+1)2+…+a9(x+1)9,且(a0+a2+…+a8)2-(a1+a3+…+a9)2=39,则实数m的值为__。
三、解答题
23.一个乒乓球队里有男队员5人,女队员4人,从中选出男、女队员各1名组成混合双打,求共有多少种不同的选法。
24.如图3所示,在A,B间有四个焊接点1,2,3,4,若焊接点脱落导致断路,则电路不通。今发现A,B之间电路不通,求焊接点脱落的不同情况共有多少种。
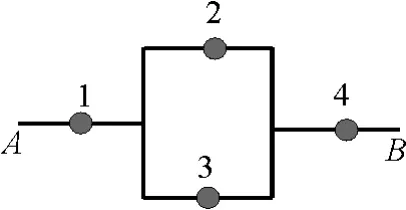
图3
27.某公司计划在北京、上海、广州、南京4个候选城市投资3个不同的项目,且在同一个城市投资的项目不超过2个,求该公司共有多少种不同的投资方案。
28.有4个不同的球,4个不同的盒子,把球全部放入盒内。
(1)恰有1个盒不放球,共有几种放法?
(2)恰有1个盒内有2个球,共有几种放法?
(3)恰有2个盒不放球,共有几种放法?

