聚焦排列组合的常考题型

■广东省汕头市澄海凤翔中学 徐春生

排列组合是高考的必考内容,一般以选择题或填空题的形式出现,它联系生活实际,生动有趣,但题型多样,思路灵活,不易掌握。因此,同学们只有掌握题型和解题方法,识别模式,熟练运用,才能顺利解题。

一、重复排列型

例15位同学报名参加两个课外活动小组,每位同学限报其中的一组,则不同的报名方法共有( )。

A.10种 B.20种

C.25种 D.32种

解析：5位同学报名参加两个课外活动小组,每位同学限报其中的一组,相当于5个不同元素没限制地安排在2个位置上,因此不同的报名方法共有25=32(种),选D。

点评：重复排列型,采用“求幂法”,即n个不同的元素没有限制地安排在m个位置上,有mn种排列方法。

二、定序型

例2由数字0、1、2、3、4、5组成没有重复数字的六位数,其中个位数字小于十位数字的六位数有 个__。(用数字作答)

解析：不考虑限制条件,由数字0、1、2、3、4、5组成没有重复数字的六位数有AA种。题中要求个位数字比十位数字小,即个位与十位上的数字一定,则所求的六位数有

点评：定序型,采用“缩倍法”,即先将n个元素进行全排列有A种,m(m≤n)个元素的全排列有A种,由于要求m个元素次序一定,因此只能取其中的某一种排法,可以利用除法起到调序的作用,即若n个元素排成一列,其中m个元素次序一定,则有种排列方法。

三、平均分组型

例3将6本不同的书分成三堆,每堆2本,则有__种不同的分法。(用数字作答)

解析：因为将6本书分成三堆,每堆2本,所以属于平均分组问题。将6本不同的书分成三堆,每堆2本,有=15(种)不同的分法。

点评：平均分组型,采用“缩倍法”,即n个不同的元素平均分成m组(m≤n,m,n可约),每组个,则有种不同的分法。

四、部分平均分组型

例4将8个球队分成3组,一组4个队,其他两组2个队,则有__种不同的分法。(用数字作答)

解析：因为将8个球队分成3组,一组4个队,其他两组2个队即可,所以属于部分平均分组问题。将8个球队分成3组,一组4个队,其他两组2个队,有=210(种)不同的分法。

点评：部分平均分组型,采用“缩倍法”,即n个不同的元素分成p组,各组中元素数目分别为m1,m2,…,mp,其中有k组的元素数目相等,则有种不同的分法。

五、分排型

例5 两排座位,第一排有3个座位,第二排有5个座位,若8名学生入座(每人一个座位),则不同的坐法种数是( )。

解析：由于8名学生入座(每人一个座位)没有限制,应是8名学生的全排列即A,故选D。

点评：分排型,采用“直排法”,即若n个元素要分m排排列,可把每排首尾连排成一列,没有其他特殊要求,则有A种排法。

六、分配型

例66人带10把铁锨参加义务劳动,每人至少带1把,有__种不同的带法。(用数字作答)

解析：把10把铁锨类比成10个相同的小球,6人类比成6个不同的盒子,将问题转化为10个相同的小球排成一排,共有9个空位,如○_○_○_○_○_○_○_○_○_○,在9个空位中插入5块隔板,把小球分成6堆,共有C=126(种)不同的方法。

点评：分配型,采用“隔板法”,即若有n个相同的小球,放入m(m≤n)个不同的盒中,每个盒中至少1个,则在n个相同的小球形成的n-1个空位中插入m-1个隔板就可保证符合题意,故共有种方法。

七、染色型

例7如图1,一个正六边形的6个区域A、B、C、D、E、F,现给这6个区域着色,要求每一个区域染一种颜色,相邻的两个区域不得使用同一颜色,现有4种不同的颜色可供选择,则有__种不同的着色方法。(用数字作答)

解析：按相间区域A、C、E染色情况分类如下：

(1)染同一色：有4×3×3×3=108(种)染法;(2)染2种不同颜色：有(CA)×3×2×2=432(种)染法;(3)染3种不同颜色：有A×2×2×2=192(种)染法。

因此,所求不同的着色方法有108+432+192=732(种)。

点评：染色型,采用“合并单元格法”,即先将能染同色的两个单元格或两个以上单元格合并成一个,再考虑其他单元格。

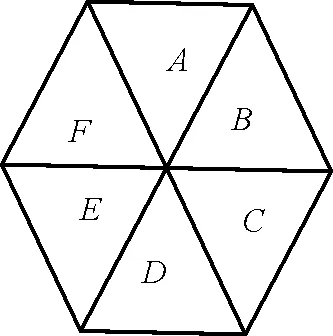
图1

八、元素个数较少型

例8 将7个相同的小球放入4个相同的盒子,每个盒子至少有1个小球,共有__种的不同放法。(用数字作答)

解析：先在每个盒子中放上1个球,剩下的3个球用列举法,如：1 1 1 0;2 1 0 0;3 0 0 0(如“3 0 0 0”表示有1个盒子放3个相同的球,其余为空盒)。

故共有3种不同的放法。

点评：元素个数较少型,采用“列举法”,可以将符合题意的元素一一列举出来。