全国名校复数测试卷
■河南省罗山县高级中学老校区 孙文成
一、选择题
A.0 B.i C.-i D.2i
A.8 B.-8 C.8i D.-8i
3.若复数(a2-3a+2)+(a-1)i是纯虚数,则实数a的值为( )。
A.1 B.2 C.1或2 D.-1
A.-2-i B.-2+i
C.2-i D.2+i
5.下面四个命题:
①0比-i大;
②两个复数互为共轭复数,当且仅当其和为实数;
③x+yi=1+i的充要条件为x=y=1;
④如果让实数a与ai对应,那么实数集与纯虚数集一一对应。
其中正确命题的个数是( )。
A.0 B.1 C.2 D.3
6.若复数z满足(3-4i)z=|4+3i|,则z的虚部为( )。
7.已知0<a<2,复数z的实部为a,虚部为1,则|z|的取值范围是( )。
A.(1,5) B.(1,3)
8.已知m∈R,若(m+mi)6=-64i,则m等于( )。
水行政执法是各级水行政主管部门和流域管理机构贯彻实施水法律法规的重要方式,是加强和创新水利社会管理、保障水利可持续发展的重要手段。加强水行政执法与刑事司法衔接机制建设,强化两者配合协调,是促进执法资源充分利用,维护良好水事秩序的重要条件和基础。但应注意到,目前我国水行政执法与刑事司法衔接机制建设整体仍然滞后,理论研究也还处于起步阶段,迫切需要结合国家政策及水利改革发展新形势新要求,加快推进水行政执法与刑事司法“两法衔接”机制建设。
9.设复数z=a+bi(a,b∈R),则z为纯虚数的必要不充分条件是( )。
A.a=0 B.a=0且b≠0
C.a≠0且b=0 D.a≠0且b≠0
10.对任意复数z=x+yi(x,y∈R),i为虚数单位,则下列结论正确的是( )。
B.z2=x2+y2
D.|z|≤|x|+|y|
11.已知复数z1=cosθ-i,z2=sinθ+i,则|z1·z2|的最大值为( )。
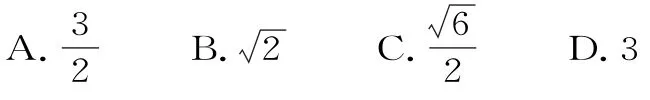
12.复数z满足条件:|2z+1|=|z-i|,那么z对应的点的轨迹是( )。
A.圆 B.椭圆
C.双曲线 D.抛物线
13.已知复数z1=a+2i,z2=-2+i,且|z1|<|z2|,则实数a的取值范围是( )。
A.(-∞,-1)∪(1,+∞)
B.(-1,1)
C.(1,+∞)
D.(0,+∞)
14.已知f(x)=x2,i是虚数单位,则在复平面内复数对应的点在( )。
A.第一象限 B.第二象限
C.第三象限 D.第四象限
15.有下面四个命题:
p1:若复数z满足∈R,则z∈R;
p2:若复数z满足z2∈R,则z∈R;
p3:若复数z1,z2满足z1z2∈R,则z1=;
p4:若复数z∈R,则∈R。
其中的真命题为( )。
A.p1,p3B.p1,p4
C.p2,p3D.p2,p4
16.如果复数z满足|z+i|+|z-i|=2,那么|z+i+1|的最小值是( )。
17.若i是虚数单位,则满足(p+qi)2=q+pi的实数p,q一共有( )。
A.1对 B.2对
C.3对 D.4对
18.复数z=-lg(x2+2)-(2x+2-x-1)i(x∈R)在复平面内对应的点位于( )。
A.第一象限 B.第二象限
C.第三象限 D.第四象限
19.设复数z+i(z∈C)在映射f下的象为复数z的共轭复数与i的积,若复数ω在映射f下的象为-1+2i,则相应的ω为( )。
A.2 B.2-2i
C.-2+i D.2+i
二、填空题
20.i+i2+i3+i4+…+i2019=__。
21.已知a,b∈R,i是虚数单位,若(1+i)(1-bi)=a,则的值为__。
24.复数z=x+yi(x,y∈R)满足|z-1|=x,则复数z对应的点Z(x,y)的轨迹方程为__。
25.复数z1=3+4i,z2=0,z3=c+(2c-6)i在复平面内对应的点分别为A,B,C,若∠BAC是钝角,则实数c的取值范围为__。
26.若复数z满足z(1+i)=1-i(i是虚数单位),则其共轭复数=__。
28.已知复数z1=-1+2i,z2=1-i,z3=3-2i,它们所对应的点分别为A,B,C。若,则x+y的值是__。
三、解答题
31.计算:

33.已知z=1+i,a,b为实数。
(1)若ω=z2+3-4,求|ω|;
34.在△ABC中,a,b,c为角A,B,C所对的边长,z1=a+bi,z2=cosA+cosBi。若复数z1·z2在复平面内对应的点在虚轴上,试判断△ABC的形状。

