一网打尽 十九类排列组合问题

■福建省泉州市第七中学 彭耿铃

求解排列、组合问题的基本思路有以下几种：

(1)限制条件,排除法：先求出不考虑限制条件的个数,然后减去不符合条件的个数,相当于减法原理;

(2)相邻问题,捆绑法：在特定条件下,将几个相关元素当作一个元素来考虑,待整体排好之后再考虑它们“内部”的排列,它主要用于解决相邻问题;

(3)插空法：先把不受限制的元素排列好,然后把特定元素插在它们之间或两端的空隙中;

(4)特殊元素、位置优先安排法：对问题中的特殊元素或位置优先排列,然后排列其他一般元素或位置;

(5)多元问题,分类法：将符合条件的排列分为几类,根据分类计数原理求出排列总数;

(6)元素相同,隔板法：若把n个不加区分的相同元素分成m组,可把n个相同元素排成一排,在元素之间插入m-1块隔板来完成分组,此法适用于同元素分组问题;

(7)“至多”“至少”,间接法：“至多”“至少”的排列、组合问题,需分类讨论且一般分类的情况较多,所以通常用间接法,它适用于反面明确且易于计算的问题;

(8)选排问题,先取再排法：选排问题很容易出现重复或遗漏,因此常先取出元素(组合)再排列,即先取后排;

(9)定序问题,消序法：甲、乙、丙顺序一定,采用消序法,用总排列数除以顺序一定的排列数;

(10)有序分配,逐分法：有序分配是指把元素按要求分成若干组,常采用逐分的方法求解。

一、特殊元素和特殊位置，优先策略

例1由0,1,2,3,4,5可以组成多少个没有重复数字的五位奇数?

解析：由于末位和首位有特殊要求,应该优先安排,避免不合要求的元素占了这两个位置。

例2(2014年四川卷)六个人从左至右排成一行,最左端只能排甲或乙,最右端不能排甲,则不同的排法共有( )。

A.192种 B.216种

C.240种 D.288种

解析：若最左端排甲,其他位置共有A=120(种)排法;若最左端排乙,最右端共有4种排法,其余4个位置有A=24(种)排法。

所以共有120+4×24=216(种)排法,故选B。

小结：位置分析法和元素分析法是解决排列组合问题最常用也是最基本的方法。若以元素分析为主,需先安排特殊元素,再处理其他元素;若以位置分析为主,需先满足特殊位置的要求,再处理其他位置。若有多个约束条件,往往是考虑一个约束条件的同时还要兼顾其他条件。

二、相邻元素，捆绑策略

例37人站成一排,其中甲乙相邻且丙丁相邻,共有多少种不同的排法?

解析：可先将甲乙两元素捆绑,并看成一个复合元素,同时丙丁也看成一个复合元素,再与其他元素进行排列,同时对相邻元素内部进行自排。由分步计数原理可得共有AAA=480(种)不同的排法。

例4(2014年北京卷)把5件不同产品摆成一排,若产品A与产品B相邻,且产品A与产品C不相邻,则不同的摆法有__种。

解析：产品A与B相邻,可把A,B捆绑,有A种方法;然后再与C以外的两件产品全排列共A种方法;最后把产品C插入,只有3个空位可选,故不同的摆法有A·A·3=2×6×3=36(种)。

小结：要求某几个元素必须排在一起,可以用捆绑法来解决问题。只需将需要相邻的元素合并为一个元素,再与其他元素一起排列,同时要注意合并元素内部也必须排列。

三、不相邻问题，插空策略

例5(2014年重庆卷)某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法种数是( )。

A.72 B.120 C.144 D.168

解析：歌舞类节目设为a1,a2,a3,小品类节目设为b1,b2,相声类节目设为c,先排a1,a2,a3不相邻,顺序如×b1×b2×c×,共AA种方法,b1b2相邻前提下×b1b2×c×插空法共AAA种方法,所以同类节目不相邻的排法种数为AA-AAA=A·(A-4)=6×20=120,故选B。

例6(2014年辽宁卷)6把椅子摆成一排,3人随机就座,任何两人不相邻的坐法种数为( )。

A.144 B.120 C.72 D.24

解析：先把3把椅子隔开摆好,它们之间和两端有4个位置,再把3人带椅子插放在4个位置,共有A=24(种)方法,故选D。

小结：元素不相邻问题可先把没有位置要求的元素进行排队,再把不相邻元素插入中间或两端。

四、定序问题，倍缩、空位插入策略

例77人排队,其中甲乙丙3人顺序一定,共有多少不同的排法?

解析：(缩倍法)对于某几个元素顺序一定的排列问题,可先把这几个元素与其他元素一起进行排列,然后用总排列数除以这几个元素之间的全排列数,则共有不同排法种数是A/A=A=840。

(空位法)设想有7把椅子让除甲乙丙以外的4人就座,共有A种方法,其余的三个位置甲乙丙共有1种坐法,则共有A=840(种)方法。

小结：解决定序问题可以用缩倍法,还可以用空位法。

五、重排问题，求幂策略

例8把6名实习生分配到7个车间实习,共有多少种不同的分法?

解析：完成此事共分六步：把第一名实习生分配到车间,有7

种分法;把第二名实习生分配到车间,也有7种分法;……依此类推,由分步计数原理知,共有76种不同的分法。

小结：允许重复的排列问题的特点是以元素为研究对象,元素不受位置的约束,可以逐一安排各个元素的位置。一般地,n个不同的元素没有限制地安排在m个位置上的排列数为mn。

六、环排问题，线排策略

例98人围桌而坐,共有多少种坐法?

解析：围桌而坐与坐成一排的不同点在于,坐成圆形没有首尾之分,所以固定1人,并从此位置把圆形展成直线,其余7人共有(8-1)!=7!(种)坐法。

小结：一般地,n个不同元素进行圆形排列,有(n-1)!种排法。如果从n个不同元素中取出m个元素进行圆形排列,共有A种排法。

七、多排问题，直排策略

例108人排成前后两排,每排4人,其中甲乙在前排,丙在后排,共有多少排法?

解析：8人排前后两排,相当于8人坐8把椅子,可以把椅子排成一排。前排2个位置上的特殊元素甲乙有A种排法,后排4个位置上的特殊元素有A种排法,其余的5人在5个位置上任意排列有A种排法,则共有AAA种排法。

故障树方法使用时间序列图和简化的故障树，并且可以集成其他任何有效可靠的方法来帮助调查人员对事故分析进入较深的程度，避免过早地停止于表面显而易见的因素。构建故障树时首先选择顶上事件，然后确定顶上事件发生的前提条件或事件，以火灾事故为例，前提条件就是点火源、可燃物和助燃物三者同时存在，它们之间的逻辑关系是与门关系。然后继续分析事件，通过逻辑关系推导直到发现基本事件，基本事件就是事故的根本原因。

小结：一般地,元素排成几排的排列问题,可归结为一排考虑,再分排研究。

八、排列组合混合问题，先选后排策略

例11有5个不同的小球,装入4个不同的盒内,每盒至少装1个球,共有多少不同的装法?

解析：第一步从5个球中选出2个组成复合元素,共有C=10(种)方法;再把4个元素(包含1个复合元素)装入4个不同的盒内,有A=24(种)方法。由分步计数原理知,装球的方法共有CA=240(种)。

小结：解决排列组合混合问题,先选后排是最基本的指导思想,此法与相邻元素捆绑策略相似。

九、小集团问题，先整体后局部策略

例12用1,2,3,4,5组成没有重复数字的五位数,其中恰有2个偶数夹在1,5这2个奇数之间,这样的五位数有多少个?

解析：把1,5,2,4当作一个小集团与3排队共有A=2(种)排法,再排小集团内部共有AA=4(种)排法。由分步计数原理知,共有AAA=8(种)排法。

小结：小集团排列问题中,先整体后局部,再结合其他策略进行处理。

十、元素相同问题，隔板策略

解析：10个名额没有差别,把它们排成一排,相邻名额之间形成9个空隙,在9个空隙中选6个位置插个隔板,可把名额分成7份,对应地分给7个班级,每一种插板方法对应一种分法,共有C=84(种)分法。

例14(2015年北京海淀区二模)某运输公司有7个车队,每个车队的车辆均多于4辆。现从这个公司中抽调10辆车,并且每个车队至少抽调1辆,那么共有__种不同的抽调方法。

解析：由于每个车队的车辆均多于4辆,只需将10个份额分成7份。相当于,将10个小球排成一排,在相互之间的9个空当中插入6个隔板,即将小球分成7份,故共有C=84(种)抽调方法。

小结：将n个相同的元素分成m份(n,m为正整数),每份至少1个元素,可以用m-1块隔板,插入n个元素排成一排的n-1个空隙中,所有分法数为

十一、正难则反，总体淘汰策略

例15(2013年四川卷)从1,3,5,7,9这五个数中,每次取出2个不同的数分别记为a,b,共可得到lga-lgb的不同值的个数是( )。

A.9 B.10 C.18 D.20

解析：lga-lgb=lg,从1,3,5,7,9中任取2个数分别记为a,b,共有A=20(种)结果,其中,故共可得到不同值的个数为20-2=18。应选C。

例16某学校安排甲、乙、丙、丁4位同学参加数学、物理、化学竞赛,要求每位同学仅报一科,每科至少有一位同学参加,且甲、乙不能参加同一学科,则不同的安排方法有__种。

解析：把四位同学分成3组,有C=6(种)分法,然后进行全排列,即CA=36,去掉甲、乙在同一组的情况。当甲、乙在一个组时,参加的方式有A=6(种),故符合题意的安排方法为36-6=30(种)。

小结：有些排列、组合问题,正面直接考虑比较复杂,而它的反面往往比较简捷,可以先求出它的反面,再从整体中淘汰。

十二、平均分组问题，除法策略

例176本不同的书平均分成3堆,每堆2本,共有多少种分法?

解析：分三堆,有CCC种方法。但这里出现重复计数的现象,不妨记6本书为ABCDEF,若第一步取AB,第二步取CD,第三步取EF,该分法记为(AB,CD,EF),则有CCC种分法。但(AB,EF,CD),(CD,AB,EF),(CD,EF,AB)(EF,CD,AB),(EF,AB,CD)这些分法仅是(AB,CD,EF)一种分法,故共有CCC/A=15(种)分法。

例18将5名同学分到甲、乙、丙3个小组,若甲小组至少2人,乙、丙组至少1人,则不同的分配方案种数为( )。

A.80 B.120 C.140 D.50

解析：先将5名同学分成3组,有两种分配方案：一是3组人数分别为2,2,1,分组方法有=15(种),然后将有2人的两组分给甲、乙或甲、丙,分配方法是15×(A+A)=60(种);二是3组人数分别为3,1,1,分组方法有=10(种),然后将1人的两组分给乙、丙两组,分配方法是10×A=20(种)。故共有60+20=80(种),选A。

小结：平均分组,不管它们的顺序如何,都是一种情况,所以分组后要一定要除以A(n为均分的组数),避免重复计数。

十三、合理分类与分步策略

例19(2012年陕西卷)两人进行乒乓球比赛,先赢3局者获胜,决出胜负为止,则所有可能出现的情形(各人输赢局次的不同视为不同情形)共有( )。

A.10种 B.15种

C.20种 D.30种

解析：由题意知比赛局数至少为3局,至多为5局。当局数为3局时,情况为甲或乙连赢3局,有2种情况;当局数为4局时,若甲赢,则前3局中甲赢2局,最后一局甲赢,共有C=3(种)情况,同理,若乙赢,也有3种情况,共有3+3=6(种)情况;当局数为5局时,前4局,甲、乙各赢2局,最后1局胜出的人赢,共有2C=12(种)情况。

综上可知,共有2+6+12=20(种)情况,选C。

例20(2015年天津五区县一模)如图1,用4种不同的颜色给图中的A,B,C,D,E,F六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法有( )。

A.288种 B.264种

C.240种 D.168种

解析：方法一,先涂A,D,E三个点,共有4×3×2=24(种)涂法,然后再按B,C,F的顺序涂色,分为两类：一类是B与E或D同色,共有2×(2×1+1×2)=8(种)涂法;另一类是B与E或D不同色,共有1×(1×1+1×2)=3(种)涂法。

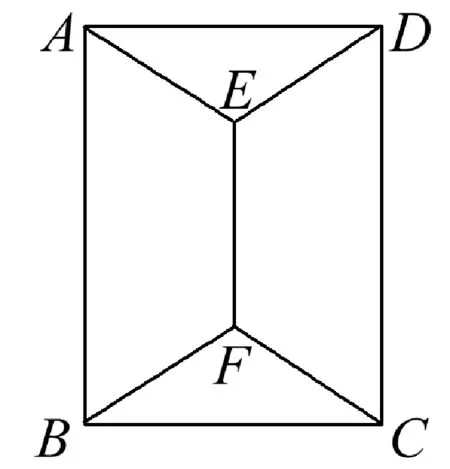
图1

所以涂色方法共有24×(8+3)=264(种),选B。

方法二,按使用颜色种数分类：

①三色涂完,必然两两同色,即A与C,B与E,D与F或A与F,B与D,C与E,有2A=48(种)涂法;

综上,涂色方法共有48+216=264(种),选B。

小结：解含有约束条件的排列、组合问题,可按元素的性质进行分类,按事件发生的过程分步,做到标准明确,分步层次清楚,不重不漏,分类标准一旦确定要贯穿解题过程的始终。

十四、构造模型策略

例21马路上有编号为1,2,3,4,5,6,7,8,9的9盏路灯,现要关掉其中的3盏,但不能关掉相邻的2盏或3盏,也不能关掉两端的2盏,求满足条件的关灯方法有多少种。

解析：把此问题当作一个排队模型,在6盏亮灯的5个空隙中插入3个不亮的灯,有C=10(种)关法。

小结：一些不易理解的排列组合题,如果能转化为非常熟悉的模型,如占位填空模型,排队模型,装盒模型等,就可使问题直观解决。

十五、实际操作穷举对应策略

例22设有编号1,2,3,4,5的5个球和编号1,2,3,4,5的5个盒子,现将5个球投入这5个盒子内,要求每个盒子放1个球,并且恰好有2个球的编号与盒子的编号相同,有多少投法?

解析：从5个球中取出2个与盒子对号有C=10(种)方法。还剩下3个球与3个盒序号不能对应,利用实际操作法,如果剩下3,4,5号球,3,4,5号盒,3号球装4号盒时,则4,5号球有只有1种装法,同理3号球装5号盒时,4,5号球有也只有1种装法,由分步计数原理有2C=20(种)装法。

小结：对于条件比较复杂的排列、组合问题,不易用公式进行运算,可利用穷举法或画出树状图,会收到意想不到的结果。

十六、分解与合成策略

例2330030能被多少个不同的偶数整除?

解析：把30030分解成质因数的乘积形式30030=2×3×5×7×11×13。

依题意可知,偶因数必先取2,再从其余5个因数中任取若干个组成乘积,所有的偶因数为：C+C+C+C+C=31。

例24正方体的8个顶点可连成多少对异面直线?

解析：我们先从8个顶点中任取4个顶点构成四面体,共有C-12=58(种)方法。每个四面体有3对异面直线,正方体中的8个顶点可连成3×58=174(对)异面直线。

例25(2014年安徽卷)从正方体六个面的对角线中任取两条作为1对,其中所成的角为60°的共有( )。

A.24对 B.30对

C.48对 D.60对

解析：方法一：与正方体的一个面上的一条对角线成60°角的对角线有8条,故共有8对,正方体的12条面对角线共有8×12=96(对),且每对均重复计算一次,故有=48(对)对角线满足题意。

方法二：正方体的面对角线共有12条,两条为一对,共有12×11÷2=66(对)。同一面上的对角线不满足题意,对面的面对角线也不满足题意,一组平行平面共有6对不满足题意的对角线对数,所以不满足题意的共有3×6=18(对)。从正方体六个面的对角线中任取两条作为一对,其中所成的角为60°的共有66-18=48(对)。

小结：分解与合成策略是排列、组合问题的一种最基本的解题策略,把一个复杂问题分解成几个小问题逐一解决,然后依据问题分解后的结构,用分类计数原理和分步计数原理将问题合成,从而得到问题的答案,每个比较复杂的问题都要用到这种解题策略。

十七、化归策略

例2625人排成5×5方阵,现从中选3人,要求3人不在同一行也不在同一列,不同的选法有多少种?

解析：将这个问题退化成9人排成3×3方阵,现从中选3人,要求3人不在同一行也不在同一列,有多少选法?这样每行必有1人从其中的一行中选取1人后,把这人所在的行列都划掉,如此继续下去。从3×3方队中选3人的方法有CCC=6(种)。再从5×5方阵选出3×3方阵便可解决问题,从5×5方队中选取3行3列有CC=100(种)选法,所以从5×5方阵选不在同一行也不在同一列的3人有CCCCC=600(种)选法。

例27(2016年新课标Ⅱ卷)如图2,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为( )。

图2

A.24 B.18 C.12 D.9

解析：由题意知,从E到F的最短路径走4步,其中必须向右2步,故从E到F的最短路径有C=6(条),从F到G的最短路径走3步,其中必须向右2步,故从F到G的最短路径有C=3(条),根据分步乘法计数原理知,共有6×3=18(条)最短路径,选B。

小结：处理复杂的排列、组合问题时,可以把一个问题退化成一个简单的问题,通过这个简单的问题的解决找到解题方法,从而进一步解决原来的问题。

十八、数字排序问题查字典策略

例28(2015年四川卷)用数字0,1,2,3,4,5组成没有重复数字的5位数,其中比40000大的偶数共有( )。

A.144个 B.120个

C.96个 D.72个

解析：首位是4时,比40000大的偶数有2×4×3×2=48(个);首位是5时,比40000大的偶数有3×4×3×2=72(个)。

综上,共有48+72=120(个)满足题意的数,选B。

小结：数字排序问题可用查字典法,查字典的法应从高位向低位查,依次求出其符合要求的个数,根据分类计数原理求出其总数。

十九、住店法策略

例297名同学争夺五项冠军,每项冠军只能由一人获得,获得冠军的可能的种数为__。

解析：因同一同学可以同时夺得n项冠军,故同学可重复排列,将7名学生看作7家“店”,五项冠军看作5名“客”,每个“客”有7种住宿法,由乘法原理知,有75种可能。

小结：解决“允许重复排列问题”要注意区分两类元素：一类元素可以重复,另一类不能重复,把不能重复的元素看作“客”,能重复的元素看作“店”,再利用乘法原理直接求解。

排列、组合是学习中的难点,同学们只要对基本的解题策略熟练掌握,就可以选取不同的技巧来解决问题。对于一些比较复杂的问题,我们可以将几种策略结合起来应用,把复杂的问题简单化。请对以上排列、组合的几种常见的解题策略加以复习巩固,做到举一反三,触类旁通,进而为后续的学习打下坚实的基础。

注：本文为泉州市教育科学“十三五”规划(第二批)课题《基于核心素养的高中数学建模教学实践研究》(课题编号：QG1352-111)的研究成果。