浅析导数应用中的几种数学思想
■安徽省利辛高级中学 胡 彬
数学家华罗庚先生说过:数学是一个原则,无数内容,一种方法,到处可用。数学思想是高中数学的灵魂,也是数学知识的精髓。在学习导数的过程中,同学们若能灵活运用相关的数学思想,往往能迅速、准确地找到解题思路,从而获解。
一、函数思想
函数思想是用运动和变化的观点去分析和研究数学问题中的数量关系,是对函数概念的本质认识。它是先建立函数关系或构造函数,再运用函数的图像和性质去分析问题、转化问题,最后使问题获得解决的一种数学思想。导数问题蕴含着函数思想,解题时若能灵活运用这种思想,就能使问题顺利解决。
例1设函数f(x)满足x2f'(x)+,则x>0时,f(x)( )。
A.有极大值,无极小值
B.有极小值,无极大值
C.既有极大值又有极小值
D.既无极大值也无极小值
解析:由题意知令g(x)=ex-2x2f(x),则g'(x)=ex-2x2f'(x)-4xf(x)=ex-由g'(x)=0,得x=2。当0<x<2时,g'(x)<0,g(x)单调递减;当x>2时,g'(x)>0,g(x)单调递增。故g(x)min=g(2)=0。则当x>0时,f'(x)≥0,故f(x)在x∈(0,+∞)上单调递增,既无极大值也无极小值,应选D。
评注:通过构造函数g(x),运用函数g(x)的函数性质,从而得到x>0时,f(x)单调递增。
二、方程思想
方程思想就是分析数学问题中变量间的等量关系,建立方程或方程组,或构造方程,再通过解方程或方程组,或者运用方程的性质去分析、转化问题,使问题获得解决。
例2若函数f(x)、g(x)分别为R上的奇函数、偶函数,且满足f(x)-g(x)=ex,则有( )。
A.f(2)<f(3)<g(0)
B.g(0)<f(3)<f(2)
C.f(2)<g(0)<f(3)
D.g(0)<f(2)<f(3)
解析:对于f(x)-g(x)=ex,以-x代替x得到f(-x)-g(-x)=e-x。又f(x)为奇函数,g(x)为偶函数,所以上式可化为-f(x)-g(x)=e-x,从而则0恒成立,所以f(x)在定义域R上为增函数,0=f(0)<f(2)<f(3)。又g(0)=-1<0,所以g(0)<f(2)<f(3),应选D。
评注:先挖掘条件,再建立方程。
三、数形结合思想
数形结合思想是数学中重要的思想方法,许多导数问题可借助于平面直角坐标系,将数的问题转化为形的问题,从而借助于形的优势,使问题获解。
例3已知函数若函数g(x)=f(x)-a有3个零点,则实数a的取值范围是( )。

解析:当x<0时,f(x)=-(x+1)ex。f'(x)=-(2+x)ex,由f'(x)>0,得x<-2;由f'(x)<0,得x>-2。所以f(x)在(-∞,-2)上递增,在(-2,0)上递减,故且x<-1时,f(x)>0,画出y=f(x)的图像如图1所示。由图知当时,y=f(x)与y=a的图像有3个交点,即g(x)有3个零点,所以实数a的取值范围是,应选A。
评注:形如f(x)=h(x)-g(x)的零点问题常转化为两函数y=h(x)与y=g(x)的图像交点问题,然后利用数形结合求解。
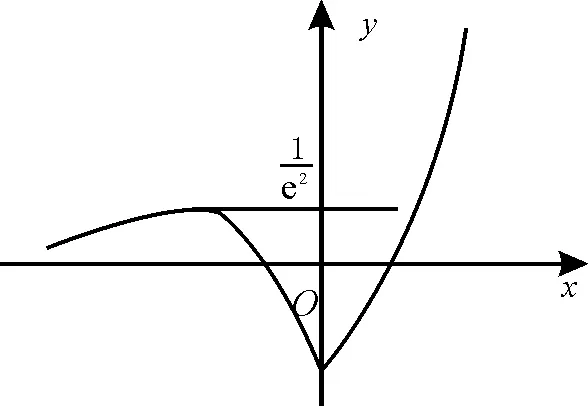
图1
四、分类讨论思想
分类讨论就是将数学对象划分为不同种类,再分别进行研究或求解的一种数学思想。通过合理的分类讨论,可以使较复杂的问题简单化。
例4设函数f(x)=1+(1+a)x-x2-x3,其中a>0。
(1)讨论f(x)在其定义域上的单调性;
(2)当x∈[0,1]时,求f(x)分别取得最大值和最小值时对应的x的值。
解析:(1)f(x)的定义域为(-∞,+∞),f'(x)=1+a-2x-3x2,令f'(x)=0,得x1
所以f'(x)=-3(x-x1)(x-x2)。
当x<x1或x>x2时,f'(x)<0;
当x1<x<x2时,f'(x)>0。
故f(x)在(-∞,x1)和(x2,+∞)上单调递减,在(x1,x2)上单调递增。
(2)因为a>0,所以x1<0,x2>0。
①当a≥4时,x2≥1,由(1)知,f(x)在[0,1]上单调递增,所以f(x)在x=0和x=1处分别取得最小值和最大值。
②当0<a<4时,x2<1,由(1)知,f(x)在[0,x2]上单调递增,在[x2,1]上单调递减,因此f(x)在处取得最大值。
又f(0)=1,f(1)=a,所以当0<a<1时,f(x)在x=1处取得最小值;当a=1时,f(x)在x=0和x=1处同时取得最小值;当1<a<4时,f(x)在x=0处取得最小值。
评注:本题考查利用导数求函数的单调区间和最大(小)值,同时考查分类讨论的思想,分类讨论的关键是确定分类的标准。
五、转化与化归思想
转化与化归思想是一种重要的数学思想方法,在研究、解决数学问题时,当思维受阻或遇到困难的问题时,要善于转化问题,化难为易,化繁为简,化陌生为熟悉,即转化到另一种情境使问题得到解决,这种转化是解决问题的有效策略。
例5设x3-x2-3。
(1)如果存在x1、x2∈[0,2]使得g(x1)-g(x2)≥M成立,求满足上述条件的最大整数M;
解析:(1)存在x1、x2∈[0,2]使得g(x1)-g(x2)≥M成立,等价于[g(x1)-g(x2)]max≥M。因为g(x)=x3-x2-3,所以。由g'(x)>0,得x<0或;由g'(x)<0,得0<x<。又x∈[0,2],所以g(x)在上是单调减函数,在上是单调增函数。解得所以=1。故[g(x1)-g(x2)]max=g(x)max-所以满足条件的最大整数M=4。
min≥g(x)max。由(1)可知在上,g(x)max=g(2)=1。在≥1恒成立,等价于a≥x-x2lnx恒成立。
设h(x)=x-x2lnx,则h'(x)=1-2xlnx-x,可知h'(x)在上为单调减函数。
因此,函数h(x)=x-x2lnx在上单调递增,在[1,2]上单调递减。
所以h(x)max=h(1)=1,即a∈[1,+∞)。
评注:审题时需要深刻理解题意,对问题作等价转化,即f(x)≥g(a)对于x∈D恒成立,应求f(x)的最小值;若存在x∈D,使得f(x)≥g(a)成立,应求f(x)的最大值。

