插空法巧解题
黄旭军
上课铃响起,小张同学正想把两本课外书放到最上层书架上时,阿木老师走进了教室,大叫一声:“停!”然后拿起手机,把书架拍了下来。
各位同学看得莫名其妙。老师把拍好的照片投影出来,说:“刚才小张同学要把两本不同的课外书放在最上层的4本书中,共有几种放法?”同学们恍然大悟,原来阿木老师又想到新题了。这个题目看似简单,却有种“有力无处使”的感觉。有些同学用枚举法一个个列出来,也不敢保证是否有重复和遗漏。
阿木老师说:“其实很简单,我们只要把4本书看成5个空隙,放第一本书时,这5个空隙就是5个不同的位置!”
“哦,然后放第二本时,就有了6个空隙,就有6种了,那么一共就是5×6=30(种)!”数学课代表接着回答。
“真棒!”阿木老师点点头,“这种通过找空隙插入的方法称为插空法,其优点大家都看到了,是不是很方便啊?”阿木老师一说完,同学们纷纷恳求他传授数学“绝招”。
例1
把1、2、3、4、5组成没有重复数字且数字1、2不相邻的5位数,则所有不同排法有多少种?
观察开始
把1、2、3、4、5排成1、2不相邻且数字不重复的5位数是排列组合问题。其中,问题的关键在于1和2是不相邻的。
常规思路
我们先来思考1和2相邻的情况。当1和2相邻时,有2种排列情况:12和21。
接下来,我们把12和21当做一个整体,分别与3、4、5进行排列,共有2×4!=48(种)排法。
如果不考虑相邻的情况,共有5!=120(种)排法。
因此1、2不相邻的排法有120-48=72(种)。
另辟蹊径
下面我们来试试插空法:
先将3、4、5三个元素排定,共有3!=6(种)排法,然后再将1、2分别插入3、4、5的4个空位中,共有4×3=12(种)排法。
根据乘法原理,所有排法共有6×12=72(种)。
答:一共有72种排法。
例2
6个白球排成一队,再加3个黑球,请问一共有多少种排法?
观察开始
又是一道排列组合类的题目。这道题目很简单,但是我们解答起来比较麻烦。
常规思路
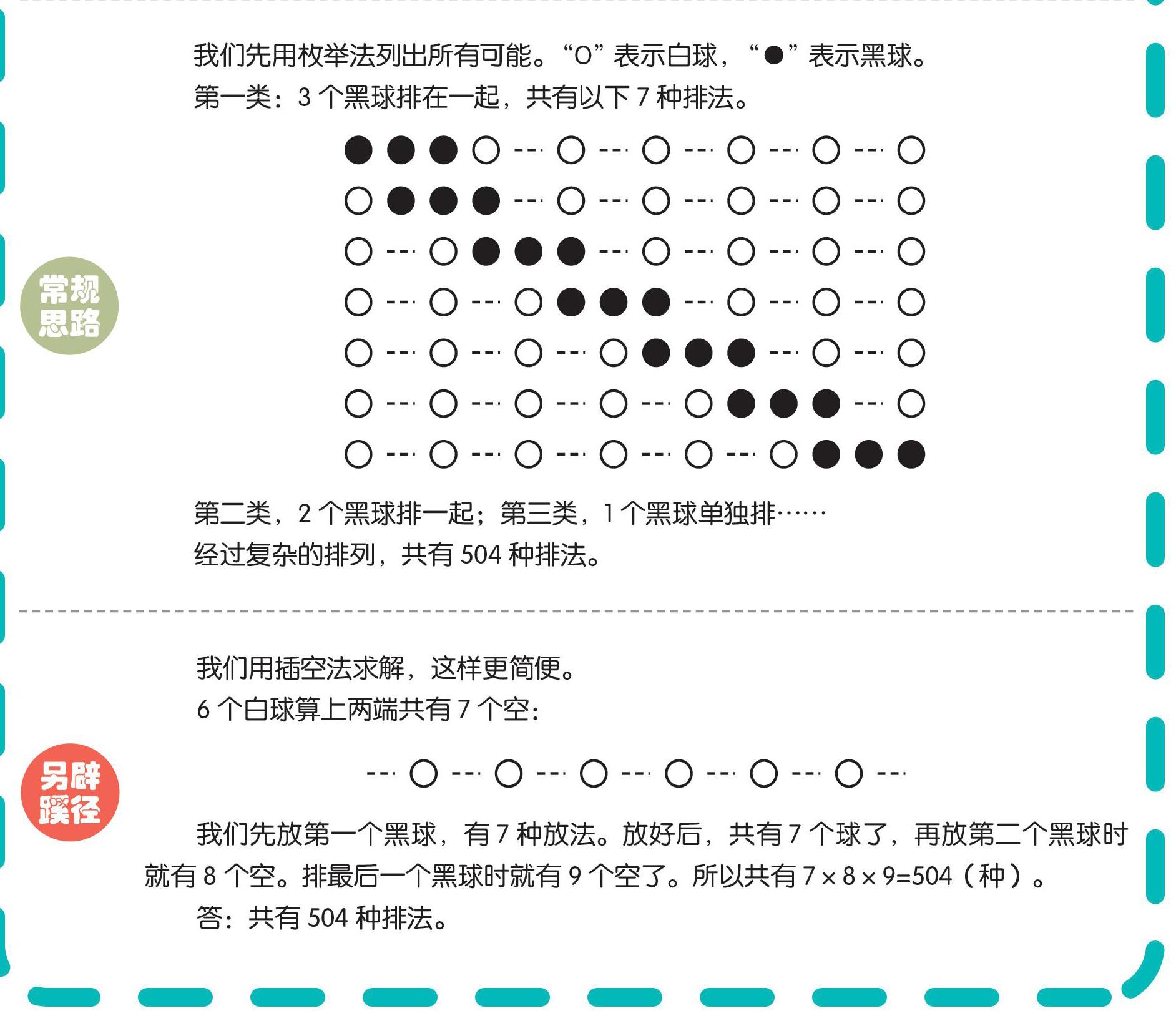
我们先用枚举法列出所有可能。“O”表示白球,“●”表示黑球。
第一类:3个黑球排在一起,共有以下7种排法。
第二类,2个黑球排一起;第三类,1个黑球单独排……
经过复杂的排列,共有504种排法。
另辟蹊径
我们用插空法求解,这样更简便。
6个白球算上两端共有7个空:
我们先放第一个黑球,有7种放法。放好后,共有7个球了,再放第二个黑球时就有8个空。排最后一個黑球时就有9个空了。所以共有7×8×9=504(种)。
答:共有504种排法。
训练一二一
在一张节目单中原有6个节目,若保持这些节目的相对顺序不变,再添加进去3个节目,则不同的添加方法共有多少种?
(答案见下期)
上期答案:1. 11厘米。2. 一组是14(2个7),33(1个11和1个3),75(2个5和1个3),169(2个13);另一组是30,35,39,143。
——对一道高考概率题的探究

