例谈极化恒等式在解高考题中的应用

江苏省扬州大学数学科学学院(225002) 陆立瑶 刘铭鑫

向量问题一直是高考的一个热点问题,而其中有关向量的数量积问题又是较难的一类.从某市高三最近几次的模考中不难看出,学生在求解数量积问题时方法欠缺,得分率较低.本文从近几年高考题出发,探索极化恒等式在解向量的数量积问题中的具体应用,以期帮助学生对此类问题形成正确的思维模式.

一.极化恒等式

设a、b是平面内的两个向量,则有(a-b)2],其几何意义是：在△ABC中,AD是BC上的中线,则有

上述式子表明向量的数量积既可以用向量的和、差的运算来表示1,同时也能用三角形内的中线长和半底边长的平方差来表示.此恒等式的精妙之处在于将向量的数量积与向量的线性运算连为一体,建立了形与数的联系.并且,在此基础上,极化恒等式可进行如下推广.

推广1a·b=

推广2在△ABC中,

推广3平面内有两个定点A,B,点P满足-→PA·--→PB=则点P的轨迹是以AB中点为圆心的圆,该圆的半径为

证明由题意可知,线段AB为定长,设AB的中点为D,则有所以又因为D是定点,P是动点,所以点P的轨迹是以AB中点为圆心、为半径的圆.

正确的使用极化恒等式的系列变式与推广,可以极大的促进问题的解决.极化恒等式蕴含着丰富的魅力,在不断的探索过程中帮助我们把握向量的本质,抓住解决向量数量积问题的方法要领.

二.极化恒等式在解题中的具体应用

1.直接利用极化恒等式的定义来解题

例1(2012年高考安徽卷)平面向量a,b满足|2a-b|≤3,则a·b的最小值为____.

解由极化恒等式可得：第一个等号当且仅当2a=-b时成立,第二个等号当且仅当|2a-b|=3时成立,两个等号可以同时成立,所以a·b的最小值为

分析这道题的常规解法是将不等式两边平方,构造出有关a·b的形式.但利用极化恒等式的定义,我们也可以将a·b先进行适当的放缩,进而表示成与2a-b有关的等式,在根据不等式的性质求解,在这里要注意等号取得的条件是否能同时满足.

2.利用极化恒等式的几何意义来解题

例2(2018年高考江苏卷)在平面直角坐标系xOy中,A为直线l:y=2x上在第一象限内的点,B(5,0),以AB为直径的圆C与直线l交于另一点D,若则点A的横坐标为____.

解设A(a,2a)(a＞0),则圆心C记AD的中点为E,连接CE,因为AC=CD且E是AD的中点,所以CE⊥AD.因为所以所以解得a=3或a=-1,因为a＞1,所以a=3.

分析此题利用极化恒等式,我们将转变成了圆心到直线的距离与半径长之比,将不方便计算的数量积问题转化为容易计算的线段长度问题,大大简化了我们的计算步骤,要注意利用好题干的隐形条件,如半径相等.

例3(2019年盐城高三期中/2013年高考浙江卷)在△ABC中,tanA=-3,△ABC的面积S△ABC=1,P0为线段BC上一定点,且满足若P为线段BC上任意一点,且恒有则线段BC的长为____.

图1

解如图1,设AC中点为E,连接P0E,过点A作AD⊥BC于点D,由极化恒等式可得因为AC为定长,所以当PE⊥BC时最小,即P0E⊥BC,又因为AD⊥BC,点E为AC中点,所以EP0是△ABC的中位线,所以DP0=CP0.又因为所以DP0=CP0=BD,因为tanC=所以tanA=tan(π-B-C)==-3,所以所以所以

分析例3是一道隐形的极化恒等式的题目,条件打破常规,其实就是让我们发现当点P在P0时,最小,这就需要我们对极化恒等式的几何意义有个更深层次的把握.当我们发现P0E⊥BC时,接下来就是与三角形面积和tanA联系起来,不难想到,直接利用三角形的面积公式,作高,从而进一步寻找到线段的长度之比.

例4 (2016年高考江苏卷)如图2,在△ABC中,D是BC的中点,E、F是AD上的两个三等分点,则的值是____.

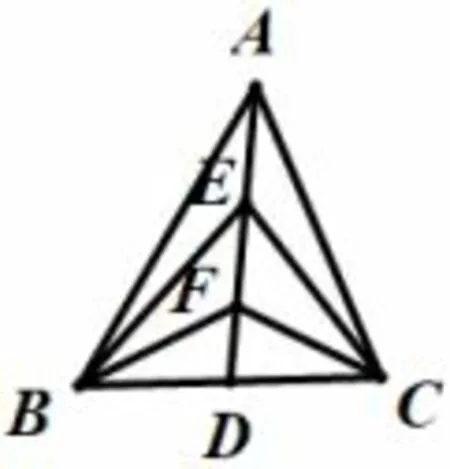
图2

解设BD=x,DF=y,根据极化恒等式,有所以

分析分析题干,AD、ED、FD分别是由外到内的三个三角形的中线,利用极化恒等式的几何意义,可以迅速构造出方程组,求解出每段长,从而计算出的值,避免了建系的繁琐.

3.利用极化恒等式的推广公式来解题

例5(2017年高考江苏卷)在平面直角坐标系xOy中,A(-12,0),B(0,6),点P在圆O:x2+y2=50上,若则点P的横坐标的取值范围是____.

解设点P坐标为(x,y),AB的中点为C,则点C(-6,3).因为=PC2-AC2≤20,所以所以点P轨迹是在以C(-6,3)为圆心,为半径的圆上及圆内.又因为点P在圆O:x2+y2=50上,所以解得又因为P在圆O左边的圆弧AB上,结合限制条件可得故点P的横坐标的取值范围是

分析例3利用向量的坐标运算也可以发现点P的轨迹,但是如果能借助极化恒等式的几何意义,就能在第一时间找到本题“题眼”所在,的P点的轨迹是“某圆圆上及内部”,只需求两个圆重合的部分.在这里要注意求出两圆交点后回到图形中,发现一些隐形的限制条件.

例6(2014年高考江苏卷)如图3,在平行四边形ABCD中,已知则的值是____.

图3

图4

解如图4,取AB中点M,连接MP,延长交直线AD于点N,所以又因为即DP为△AMN的中位线,所以AN=2AD=10,MN=2MP在△AMN中,两式相加得所以

分析这道题得常规解法是寻找基底与建系,但用极化恒等式也不失为一种巧妙的方法.先利极化恒等式计算出MP的长,进而发现线段DP与AM存在倍数关系,如若构造出三角形,则DP为△AMN的中位线,那三边长可以依次求出.通过放缩与推广2,即可快速求解出-→AB·--→AD的值.

三.解题反思

通过以上例题我们可以发现,极化恒等式在解决向量的数量积问题中具有广泛的应用,其魅力来源于它将代数与几何相连接,将抽象的数量积问题用形象的几何图形来展示,转变为我们学过的平面几何中线段长的问题,联系了学生的最近发展区.向量问题综合性强,难度大,选择合适的解题工具就显得尤为重要,在实际教学中,要让学生发现,极化恒等式是解题的利器,训练他们快速地发现图形特征,巧妙地使用极化恒等式进行探索,最终实现数与形相互转换的能力的发展.