以模型为载体解决空间几何体的外接球与内切球问题
广东省广州市真光中学(510380) 黄林盛
球是特殊的几何体,具有多方位的对称性,从而具有很多特殊的性质.在高考以空间几何体为载体的外接球和内切球问题中,因多面体有外接球或内切球是唯一的.而唯一性使得外接球问题成为每高考的热点和难点.主要考查学生空间想象能力为主线,结合边角关系、位置关系、面积与体积的计算,从而达到培养学生直观想象核心素养要求.从高三第一轮复习教学实践中,发现学生在研究空间几何体的外接球、内切球问题时,常常因缺乏空间想象力而感到束手无策.其根本原因是,除了这类题目的入手确实不易之外,主要是学生没有形成解题的模式和套路,以至于遇到类似的题目便产生畏惧心理.以下结合笔者的高三第一轮复习教学实例,给出解空间几何外接球和内切球的问题八种模型方法,供读者参考与交流.
类型一墙角模型(三条棱两两垂直,不找球心的位置即可求出球半径)
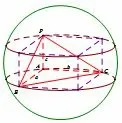
图1-1

图1-2

图1-3

图1-4
方法:找三条两两垂直的线段,直接用公式(2R)2=a2+b2+c2,即求出R.
例1在正三棱锥S-ABC中,M、N分别是棱SC、BC的中点,且AM⊥MN,若侧棱求正三棱锥S-ABC外接球的表面积?
解引理:正三棱锥的对棱互相垂直.证明如下:
如图1-5,取AB,BC的中点D,E,连接AE,CD,AE,CD交于H,连接SH,则H是底面正三角形ABC的中心,所以SH⊥平面ABC,所以SH⊥AB,因为AC=BC,AD=BD,所以CD⊥AB,所以AB⊥平面SCD,所以AB⊥SC,同理:BC⊥SA,AC⊥SB,即正三棱锥的对棱互垂直.

图1-5
本题图如图1-5,因为AM⊥MN,SB//MN,所以AM⊥SB,因为AC⊥SB,所以SB⊥平面SAC,所以SB⊥SA,SB⊥SC.因为SB⊥SA,BC⊥SA,所以SA⊥平面SBC,所以SA⊥SC,故三棱锥S-ABC的三棱条侧棱两两互相垂直,所以即4R2=36,所以正三棱锥S-ABC外接球的表面积是36π.
类型二对棱相等模型(补形为长方体)
题型:三棱锥(即四面体)中,已知三组对棱分别相等(AB=CD,AD=BC,AC=BD),求外接球半径.
第一步:画出一个长方体,标出三组互为异面直线的对棱;
第二步:设出长方体的长宽高分别为a,b,c,AD=BC=x,AB=CD=y,AC=BD=z,列方程组,

图2-1
例2在三棱锥A-BCD中,AB=CD=2,AD=BC=3,AC=BD=4,求三棱锥A-BCD外接球的表面积?
解如图2-1,设补形为长方体,三个长度为三对面的对角线长,设长宽高分别为a,b,c,则a2+b2=9,b2+c2=4,c2+a2=16,所以2(a2+b2+c2)=9+4+16=29,
类型三汉堡模型(直棱柱的外接球、圆柱的外接球)
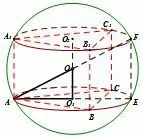
图3-1

图3-2

图3-3
题型:如图3-1,图3-2,图3-3,直三棱柱内接于球(同时直棱柱也内接于圆柱,棱柱的上下底面可以是任意三角形)
第一步:确定球心O的位置,O1是△ABC的外心,则OO1⊥平面ABC;
第二步:算出小圆O1的半径AO1=r,OO1=(AA1=h也是圆柱的高);
第三步:勾股定理:_OA2___=O1A2+O1O2⇒R2=解出R.
例3一个正六棱柱的底面上正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为底面周长为3,求这个球的体积?
解设正六边形边长为a,正六棱柱的高为h,底面外接圆的半径为r,则正六棱柱的底面积为所以也可R2=球的体积为
类型四切瓜模型(两个大小圆面互相垂直且交于小圆直径——正弦定理求大圆直径是通法)

图4-1

图4-2

图4-3

图4-4
1.如图4-1,平面PAC⊥平面ABC,且AB⊥BC(即AC为小圆的直径),且P的射影是△ABC的外心⇔三棱锥P-ABC的三条侧棱相等⇔三棱锥P-ABC的底面△ABC在圆锥的底上,顶点P点也是圆锥的顶点.
解题步骤:
第一步:确定球心O的位置,取△ABC的外心O1,则P,O,O1三点共线;
第二步:先算出小圆O1的半径AO1=r,再算出棱锥的高PO1=h(也是圆锥的高);
第三步:勾股定理:OA2=O1A2+O1O2⇒R2=(h-R)2+r2,解出R;
事实上,△ACP的外接圆就是大圆,直接用正弦定理也可求解出R.
2.如图4-2,平面PAC⊥平面ABC,且AB⊥BC(即AC为小圆的直径),且PA⊥AC,则利用勾股定理求三棱锥的外接球半径:

3.如图4-3,平面PAC⊥平面ABC,且AB⊥BC(即AC为小圆的直径).

4.题型:平面PAC⊥平面ABC,且AB⊥BC(即AC为小圆的直径).
第一步:易知球心O必是△PAC的外心,即△PAC的外接圆是大圆,先求出小圆的直径AC=2r;
第二步:在△PAC中,可根据正弦定理求出R.
例4一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,求该正三棱锥的体积?
解高h=R=1,底面外接圆的半径为R=1,直径为2R=2,设底面边长为a,则三棱锥的体积为
类型五垂面模型(一条直线垂直于一个平面)
1.题型:如图5-1,PA⊥平面ABC,求外接球半径.
解题步骤:
第一步:将△ABC画在小圆面上,A为小圆直径的一个端点,作小圆的直径AD,连接PD,则PD必过球心O;

图5-1
第二步:O1为△ABC的外心,所以OO1⊥平面ABC,算出小圆O1的半径O1D=r(三角形的外接圆直径算法:利用正弦定理,得
第三步:利用勾股定理求三棱锥的外接球半径:

2.题型:如图5-2至5-8这七个图形,P的射影是△ABC的外心⇔三棱锥P-ABC的三条侧棱相等⇔三棱锥P-ABC的底面△ABC在圆锥的底上,顶点P点也是圆锥的顶点.

图5-2

图5-3

图5-4

图5-5

图5-6

图5-7

图5-8
解题步骤:
第一步:确定球心O的位置,取△ABC的外心O1,则P,O,O1三点共线;
第二步:先算出小圆O1的半径AO1=r,再算出棱锥的高PO1=h(也是圆锥的高);
第三步:勾股定理:OA2=O1A2+O1O2⇒R2=(h-R)2+r2,解出R.
方法二:小圆直径参与构造大圆,用正弦定理求大圆直径得球的直径.
例5一个几何体的三视图如图所示,求该几何体外接球的表面积?

图5-9

图5-10
解如图5-10所示,
法一(勾股定理)利用球心的位置求球半径,球心在圆锥的高线上,
法二(大圆法求外接球直径)如图,球心在圆锥的高线上,故圆锥的轴截面三角形PMN的外接圆是大圆,于是下略;
类型六折叠模型
题型:两个全等三角形或等腰三角形拼在一起,或菱形折叠(如图6-1)

图6-1
第一步:先画出如图6-1所示的图形,将△BCD画在小圆上,找出△BCD和△A′BD的外心H1和H2;
第二步:过H1和H2分别作平面BCD和平面A′BD的垂线,两垂线的交点即为球心O,连接OE,OC;
第三步:解△OEH1,算出OH1,在Rt△OCH1中,勾股定理:OH21+CH21=OC2.
注:易知O,H1,E,H2四点共面且四点共圆,证略.
例6 在边长为的菱形ABCD中,∠BAD=60°,沿对角线BD折成二面角A-BD-C为120°的四面体ABCD,求此四面体的外接球表面积?
解如图6-2,取BD的中点M,△ABD和△CBD的外接圆半径为r1=r2=2,△ABD和△CBD的外心O1,O2到弦BD的距离(弦心距)为d1=d2=1,

图6-2
法一:四边形OO1MO2的外接圆直径OM=2,
法三:作出△CBD的外接圆直径CE,则AM=CM=3,CE=4,ME=1,AE=cos∠AEC=sin∠AEC=
类型七两直角三角形拼接在一起(斜边相同,也可看作矩形沿对角线折起所得三棱锥)模型
题型:如图7-1,∠APB=∠ACB=90°,求三棱锥PABC外接球半径(分析:取公共的斜边的中点O,连接OP,OC,则OA=OB=OC=OP=所以O为三棱锥P-ABC外接球球心,然后在OCP中求出半径),当看作矩形沿对角线折起所得三棱锥时与折起成的二面角大小无关,只要不是平角,球半径都为定值.

图7-1
例7在矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B-AC-D,求四面体ABCD的外接球的体积?
解2R=AC=5,R=
类型八锥体的内切球问题
1.题型:如图8-1,三棱锥P-ABC上正三棱锥,求其内切球的半径.
第一步:先现出内切球的截面图,E,H分别是两个三角形的外心;
第三步:由△POE相似于△PDH,建立等式:解出r.
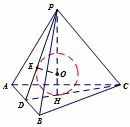
图8-1

图8-2
2.题型:如图8-2,四棱锥P-ABCD是正四棱锥,求其内切球的半径
第一步:先画出内切球的截面图,P,O,H三点共线;
第三步:由△POG相似于△PFH,建立等式:解出r.
3.题型:三棱锥P-ABC是任意三棱锥,求其的内切球半径
方法:等体积法,即三棱锥的体积可以表示成:内切球球心为顶点,分别以四个面为底面所构成的四个三棱锥的体积之和.
第一步:先画出四个表面的面积和整个锥体体积;
第二步:设内切球的半径为r,建立等式:
例8正四棱锥S-ABCD的底面边长为2,侧棱长为3,求其内切球的半径?
解如图8-3,正四棱锥S-ABCD的高正四棱锥S-ABCD的体积为侧面斜高正四棱锥S-ABCD的表面积为正四棱锥S-ABCD的体积为所以

图8-3
空间几何本外接球和内切球的问题,考查了根据图形想象出直观形象;能正确地分析出图形中的基本元素及其相互关系;能对图形进行分解、组合;会运用图形与图表等手段形象地揭示问题的本质,很符合数学学科六大核心素养的培养.数学的学习过程应立足于提高抽象概括能力、推理论证能力、空间想象能力、数学建模能力、运算求解能力、数据处理能力实践与探究,.更应该贯穿整个高三复习.本文通过以模型为载体解决空间几何体的外接球与内切球问题的归纳总结与反思,不仅帮助学生解决了球体的热点难点问题,更让在学生在学习过程中,进一步发展几何直观和空间想象能力,增强运用图形和空间想象思考问题的意识,提升数形结合的能力,感悟事物的本质,培养创新思维,直观想象核心素养的探究过程中得到培养.

