一道椭圆试题的解法挖掘与性质推广*—以2018年浙江高考填空压轴题为例

广东省广州市第十六中学(510080) 温伙其

直线与圆锥曲线的位置关系,是每年高考必考知识.既可从代数角度入手解题,也可研究几何特征入手解题;常常联立直线与圆锥曲线得到x(y)的一元二次方程,用韦达定理设而不求解题;而对于涉及长度或角度问题的处理,引入椭圆或直线的参数方程或极坐标方程,用极径极角的几何意义解题则可大大减小运算量;甚至还可适当借助圆锥曲线常用的二级结论,丰富解题策略;题目一般都可从一种曲线推广到另外两种曲线,从特殊情况延伸到一般情况,适合教学过程的深入探讨挖掘拓展.下面以2018年浙江高考数学试题第17题为例进行阐述：

题目已知点P(0,1),椭圆上两点A,B满足则当m=______时,点B横坐标的绝对值最大.

解法分析

思路一直线与圆锥曲线位置关系的处理,通性解法为：联立它们的方程,得到x或y的一元二次方程,则有“根与系数的关系”,再把条件-→AP=2--→PB相应转化为x(y)的关系式,和韦达定理共同构造三元方程组,即可构造m和x1、x2之间的关系式.

解法1由题意知直线过点P,当AB斜率存在时设为k,则直线AB的方程为y=kx+1.联立直线和椭圆方程得(1+4k2)x2+8kx+4-4m=0,设A(x1,y1),B(x2,y2),则有

∆=4k2m+m-1＞0.由得x1=-2x2,联立(1)解得所以当且仅当时取等号,即时|x2|max=2,x1=-2x2.联立(2)解得即-2x22·(1+4k2)=4-4m,又因为当取得最大值2,把代入上式,解得m=5,即m=5时,|x2|取得最大值2;当AB斜率不存在时,即AB为y轴,此时由得解得m=9,即m=9时x2=0;综上,可知当m=5时,|x2|取得最大值2.

思路二条件隐含A、B两点坐标之间的线性数量关系,可用其中一点的坐标表示另外一点的坐标,又知A、B两点在椭圆上,把它们代入椭圆方程即可再消元,进而得到与m与x或y之间的关系式.

解法2 设A(x1,y1),B(x2,y2),由有(-x1,1-y1)=2(x2,y2-1),即将点A代入椭圆方程有x21+4y21=4m,消元x1得x22+y21=m;将点B代入椭圆方程有x22+4y22=4m,两式相减得(y1+2y2)(y1-2y2)=-3m,整理得y1-2y2=-m,结合y1=3-2y2,解得因此x22=m-y21=所以当m=5时,x22取得最大值4,即当m=5时|x2|取得最大值为2.

思路三直线AB解析式,除了解析几何的方法,还可引入它的参数方程或极坐标方程,把问题转化为三角函数关系,借助均值定理或三角函数的有界性求解最值,开辟直线与圆锥曲线位置关系解题的另一蹊径.此思路对某些涉及参数的长度意义,如垂直、弦长问题时,能起到事半功倍的效果.

解法3设直线AB的倾斜角为α(α≠0),则直线AB的参数方程为(t为参数),A,B两点对应的参数分别为t1,t2,把直线AB参数方程代入椭圆,得(cos2α+4sin2α)t2+8sinα·t+4-4m=0,则

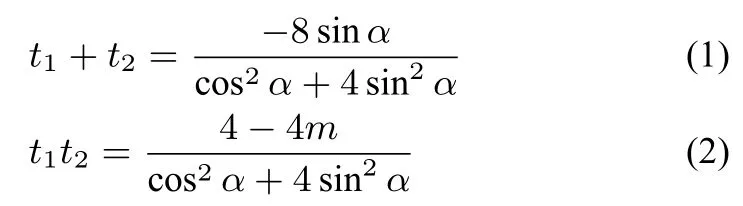
∆=4msin2α+(m-1)cos2α＞0.由得t1=-2t2,联立(1)解得即时,|xB|=|t2cosα|=当且仅当cos2α=4sin2α时取等号,即当cos2α=4sin2α时|xB|取得最大值2,此时所以不妨取B(2,2),代入椭圆解得m=5,即当m=5时|x2|取得最大值为2;当时,所以xB=tcosα=0,yB=1+t2sinα=1+2=3,代入椭圆方程,解得m=9,即m=9时xB=0;综上,可知当m=5时,|x2|取得最大值为2.

思路四涉及圆锥曲线的中点弦,自然会选择点差法解题,进而拓展延伸就可得到椭圆弦AB的中点结论(M为弦AB的中点),灵活运用此特殊结论,既可多角度解题,又可简化运算过程.

解法4由题意知直线过点P,当AB斜率存在时设为k,则直线AB的方程为y=kx+1,设A(x1,y1),B(x2,y2),AB的中点为M,由得x1=-2x2,所以xM=代入y=kx+1解得由点差法结论知即整理得当且仅当所以时|x2|max=2,根据椭圆的对称性,不妨取直线AB的方程为则点B(2,2),代入椭圆解得m=5,即当m=5时,|x2|取得最大值为2;当AB斜率不存在时,解答过程同方法一,得m=9时x2=0;综上,可知当m=5时,|x2|取得最大值为2.

把上述题目条件特殊点P(0,1)进一步推广为y轴上任一点P(0,b),甚至延伸到平面内的任一点P(x0,y0),且椭圆推广为时,则有以下结论：

结论1 已知点P(0,b),椭圆m＞1)上两点A,B满足则m的取值范围是且当时,点B横坐标的绝对值的最大值为

证明过程和本文四种解法相似,此处略.

结论2已知点P(x0,y0)在椭圆b＞0)内,其上两点A,B满足则m的取值范围是且当时,|xy0-x0y|取得的最大值为

证明设点B(x,y),则由得A((λ+1)x0-λx,(λ+1)y0-λy),把点A,B代入椭圆方程有

(1)两边乘以λ2减去(2)得即+(λ-1)m,两边平方得

由此可得

当然,我们若把试题从椭圆推广到双曲线,也会有浙江高考试题相似的特殊值,也可得到类似本文的特殊结论,限于篇幅限制,本文不做赘述,有兴趣读者,可自行探讨.