导数创新思维题——浅谈构造函数的解题策略

■河南省罗山高级中学 刘 刚

一、命题陷阱

(1)图形考虑不周；(2)思维定式(构造与等式有关的函数)；(3)已知条件中含有导函数值而无从下手；(4)错解恒成立中的最值；(5)含有导函数的式子中和差构造陷阱；(6)构造与三角函数有关的函数；(7)忽视分母造成解集不完备；(8)构造与指数函数、对数函数有关的函数。

二、典例分析

(一)图形考虑不周

例1已知，若关于x的方程f2(x)-t f(x)+t-1=0恰好有4个不相等的实数解，则实数t的取值范围为( )。

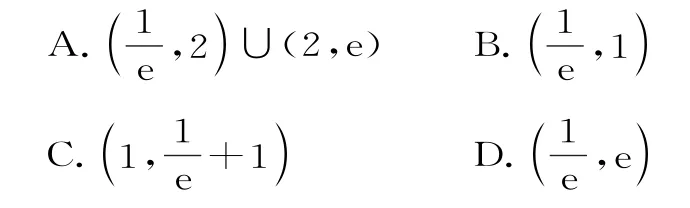
解析：

当x≥0时，

当0≤x＜1时，f'(x)＞0；当x≥1时，f'(x)≤0。

因此，f(x)在(0，1)上单调递增，在(1，+∞)上单调递减。

当x＜0时，f(x)为减函数。

作出函数f(x)的草图，如图1。

图1

设m=f(x)，当m时，方程m=f(x)有1个解。

当m=0时，方程m=f(x)有1个解；

当m＜0时，方程m=f(x)无解。

则方程f2(x)-t f(x)+t-1=0等价于m2-t m+t-1=0。

要使关于x的方程f2(x)-t f(x)+t-1=0恰好有4个不相等的实数根，等价于方程m2-t m+t-1=0有2个不同的根m1＞且

令g(m)=m2-t m+t-1=0。

陷阱预防：这类问题根据已知条件画出函数的图像，利用图像求解时注意切线的特殊位置。

方法规律：函数图像在研究零点个数、解的个数中的应用。

(1)研究两个函数图像的交点个数：在同一坐标系中分别作出两个函数的图像，利用数形结合求解。

(2)确定方程根的个数：当方程与基本函数有关时，可以通过函数图像来研究方程的根，方程f(x)=0的根就是函数f(x)的图像与x轴交点的横坐标，方程f(x)=g(x)的根就是函数f(x)与g(x)对应图像交点的横坐标。

(3)研究不等式的解：当不等式问题不能用代数法求解，但其对应函数的图像可作出时，常将不等式问题转化为两个函数图像的上、下位置关系问题，从而利用数形结合求解。

(二)思维定式陷阱

例2若函数f(x)满足x f'(x)-f(x)=x3ex，且f(1)=0，则当x＞0时，f(x)( )。

A.有极大值，无极小值

B.有极小值，无极大值

C.既有极大值又有极小值

D.既无极大值又无极小值

解析：由题设知，当x＞0时

由f(1)=0，得c=0。

所以f(x)=x(x-1)ex。

又f'(x)=(x2+x-1)ex，可令f'(x)=0，解得或(舍去)。

因此，当x＞0时，f(x)有极小值无极大值。

故选B。

陷阱预防：这类问题在构造函数时，注意逆向思维，构造出原函数的导函数与已知条件相同，或者能够利用已知条件求解。

(三)利用已知条件，先求导，再求解

例3已知函数f(x)在R上可导，且f(x)=2x+f'(0)·(x2-1)，则f(0)的值为( )。

A.l n2 B.0 C.1 D.1-l n2

解析：由f(x)=2x+f'(0)·(x2-1)，可得f'(x)=2xl n2+f'(0)·2x。

令x=0，得f'(0)=l n2。

令x=0，代入原式得f(0)=1-l n2，故选D。

陷阱预防：根据已知条件先求特殊值的导函数值，再求解否则无法解出正确答案。

(四)导函数式子中有和差，构造时需谨慎

例4函数f(x)在其定义域内满足x f'(x)+f(x)=ex，其中f'(x)为函数f(x)的导函数，且f(1)=e，则函数f(x)( )。

A.有极大值，无极小值

B.有极小值，无极大值

C.既有极大值又有极小值

D.既无极大值又无极小值

解析：由x f'(x)+f(x)=ex，可得

(x f(x))'=(ex)'。

令x f(x)=ex+c，又f(1)=e，故c=0。

故f(x)在(-∞，0)上单调递减，(0，1)上单调递减，(1，+∞)上单调递增，f(x)在x=1处取得极小值，无极大值。

故选B。

陷阱预防：导函数式子中有和差结构，一般情况下，和考虑构造函数的积，差考虑构造函数的商。

(五)构造与三角函数有关的函数

故

例5定义在上的可导函数f(x)的导数为f'(x)，且f'(x)c o sx+f(x)s i nx＜0，f(0)=0，则下列判断中，一定正确的是( )。

解析：设

因此，F(x)在上单调递减。

故选A。

陷阱预防：构造函数时注意正弦、余弦的导数公式，尤其注意余弦的导数公式的符号。

方法规律：根据含导函数的不等式构造原函数时，常见的类型有：

①原函数是函数和差的形式；

②原函数是函数乘除的形式；

③原函数是函数与x的乘除的形式；

④原函数是函数与ex的乘除的形式；

⑤原函数是函数与s i nx(c o sx)的乘除的形式；

⑥原函数是函数与l nx的乘除的形式。

(六)忽视分母造成解集不完备

例6已知函数f(x)是定义在(0，+∞)的可导函数，f'(x)为其导函数，当x＞0且x≠1时若曲线y=f(x)在x=1处的切线的斜率为则f(1)=( )。

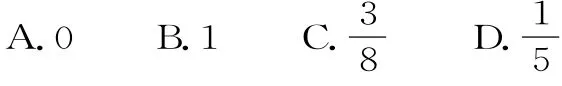
解析：当x＞0且x≠1时＞0，可得：

当x＞1时，2f(x)+x f'(x)＞0；

当0＜x＜1时，2f(x)+x f'(x)＜0。

令g(x)=x2f(x)，x∈(0，+∞)。

g'(x)=2x f(x)+x2f'(x)=x·(2f(x)+x f'(x))。

因此，当x＞1时，g'(x)＞0；当0＜x＜1时，g'(x)＜0。

函数g(x)在x=1处取得极值。

故g'(1)=2f(1)+f'(1)=0。又f'(1)=，故

故选C。

陷阱预防：解答时，要讨论分母的正负。

方法规律：求解这类问题一定要耐心审题、读懂题，通过对问题的条件和结论进行类比、联想、抽象、概括，准确构造出符合题意的函数。解这类不等式的关键点就是构造合适的函数，构造函数时往往从两方面着手：①根据导函数的“形状”变换不等式“形状”；②若是选择题，可根据选项的共性归纳构造恰当的函数。本题根据①，联想到函数g(x)=x2f(x)，再结合条件判断出其单调性，进而得出正确结论。

(七)构造与指数函数、对数函数有关的函数

例7定义在R上的函数f(x)与其导函数f'(x)满足：f(x)+f'(x)＞e1-x，则下列不等式一定成立的是( )。

A.f(0)+e＜ef(1)

B.f(0)+e＞ef(1)

C.f(0)+e＜f(1)

D.f(0)+e＞f(1)

解析：由f(x)+f'(x)＞e1-x，可得ex(f(x)+f'(x))-e＞0。

令g(x)=exf(x)-ex，则g'(x)=ex[f(x)+f'(x)]-e＞0。

故函数g(x)在R上为增函数。

则g(1)＞g(0)，即ef(1)-e＞f(0)。

整理得f(0)+e＜ef(1)，故选A。

陷阱预防：构造函数时注意两种情况：原函数是函数与ex的乘除的形式；原函数是函数与l n

x的乘除的形式。

方法规律：解答这类题的关键是构造函数，主要考查导数运算法则的逆用。

三、跟踪练习

1.函数f(x)的导函数为f'(x)，满足，且则f(x)的极值情况为( )。

A.有极大值，无极小值

B.有极小值，无极大值

C.既有极大值又有极小值

D.既无极大值也无极小值

解析：因为所以x2f'(x)+2x f(x)=l nx。

故[x2f(x)]'=l nx。

则x2f(x)=xl nx-x+c。

将x=e代入上式得e2f(e)=e l ne-e+c。

令g(x)=-xl nx+2x-e，则g'(x)=1-l nx。当x∈(0，e)时，g'(x)＞0；当x∈(e，+∞)时，g'(x)＜0。故当x=e时，g(x)取得最大值0，则g(x)≤0恒成立，f'(x)≤0恒成立。所以f(x)既无极大值也无极小值，选D。

2.已知定义在R上的奇函数f(x)的导函数为f'(x)，当x＜0时，f(x)满足：2f(x)+x f'(x)＜x f(x)，则f(x)在R上的零点个数为( )。

A.5 B.3 C.1或3 D.1

解析：根据题意可构造函数F(x)=

则F'(x)

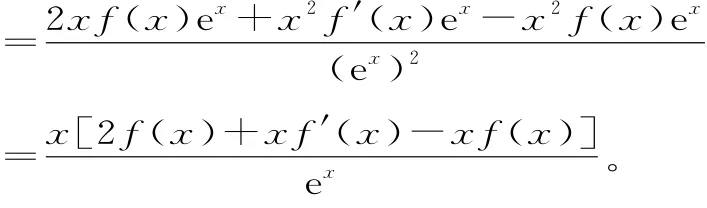
由题知当x＜0时，f(x)满足：2f(x)+x f'(x)＜x f(x)，故F'(x)＞0。

因此，当x＜0时，函数F(x)是增函数。

又因为F(0)=0，所以当x＜0时，F(x)＜F(0)=0成立。

因为f(x)是奇函数，所以x＞0时，f(x)＞0。

因此，f(x)=0只有一个根就是0。

故选D。

3.定义在上的函数y=f(x)满足：f(x)＞f'(x)t a nx恒成立，则下列不等式中成立的是( )。

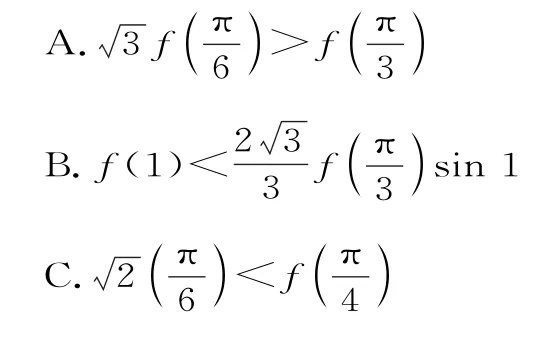
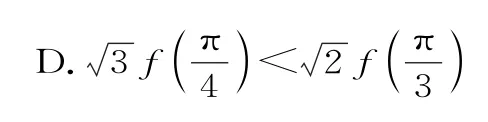
解析：因为所以s i nx＞0，c o sx＞0。

由f(x)-f'(x)t a nx＞0，得f(x)c o sx＞f'(x)s i nx。

g(1)＞，故B错误。

g，故C错误。

同理，D也错误。

故答案为A。

4.已知定义在(0，+∞)上的函数f(x)的导数为f'(x)，且满足f'(x)·(xl nx2)＞2f(x)，则( )。

A.6f(e)＞2f(e3)＞3f(e2)

B.6f(e)＜3f(e2)＜2f(e3)

C.6f(e)＞3f(e2)＞2f(e3)

D.6f(e)＜2f(e3)＜3f(e2)

解析：令则g'(x)=

故g(x)在(0，+∞)上递增，g(e)＜g(e2)＜g(e3)。

整理得6f(e)＜3f(e2)＜2f(e3)。

故选B。

5.设函数f(x)是定义在(-∞，0)上的可导函数，其导函数为f'(x)，且有x f'(x)＜3f(x)，则不等式8f(x+2019)+(x+2019)3·f(-2)＞0的解集为( )。

A.(-∞，-2021)

B.(-2021，0)

C.(-2021，-2019)

D.(-∞，-2022)

解析：函数f(x)是定义在(-∞，0)上的可导函数，其导函数为f'(x)，且有x f'(x)＜3f(x)。因为x＜0，所以x2f'(x)-3x f(x)＞0。设则当x＜0时，F'(x)＜0，即F(x)在(-∞，0)上是减函数。

不等式8f(x+2019)+(x+2019)3·f(-2)＞0等价于F(x+2019)-F(-2)＜0，也即F(x+2019)＜F(-2)。因为F(x)在(-∞，0)上是减函数，所以x+2019＞-2，即x＞-2021。又因为f(x)的定义域为(-∞，0)，所以x+2019＜0，x＜-2019。

不等式8f(x+2019)+(x+2019)3·f(-2)＞0的解集为(-2021，-2019)，故选C。

6.已 知 函 数f(x)=若不等式f(x)≤4-m x恒成立，则实数m的取值范围是( )。

A.[2，+∞) B.[-2，0)

解析：如图2，画出函数f(x)=的图像。

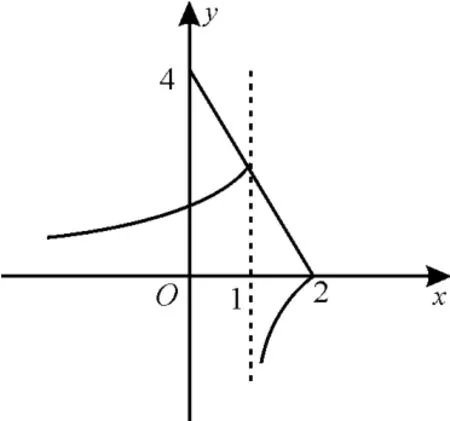
图2

由y=4-m x可知直线在y轴上的截距为4。

若f(x)≤4-m x恒成立，即y=4-m x的图像恒在分段函数f(x)的上方，故0≥-m≥-2⇒0≤m≤2。

故选D。