推理与证明问题突破方法

■河南省罗山高级中学 程传敏

一、推理有门路

与图形有关的推理是合情推理中非常重要的内容。对于这类题型，我们可以从多个角度进行分析。例如观察几组图形的变化规律、几组图形的数字规律、每个图形的结构等。

例1分形几何学是数学家伯努瓦·曼德尔布罗在20世纪70年代创立的一门新的数学学科，它的创立为解决传统科学众多领域的难题提供了全新的思路。按照如图1所示的分形规律可得如图2所示的一个树形图。若记图2中的第n行黑圈的个数为an，则a2019=_________。

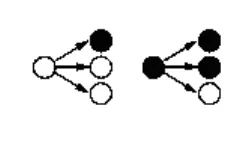
图1

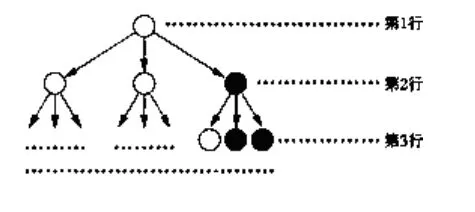
图2

【理解题意】由图1所示的分形规律，可知1个白圈分形为2个白圈1个黑圈，1个黑圈分形为1个白圈2个黑圈。

解法一：若某行白圈x个，黑圈y个，此行记为(x，y)。

则第1行记为(1，0)，第2行记为(2，1)，第3行记为(5，4)，第4行的白圈数为2×5+4=14，黑圈数为5+2×4=13，所以第4行的“坐标”为(14，13)，同理可得第5行的“坐标”为(41，40)，第6行的“坐标”为(122，121)，…。各行黑圈数乘2，分别是0，2，8，26，80，…即1-1，3-1，9-1，27-1，81-1，…，所以可以归纳出第n行黑圈数(n∈N*)，所以

解法二：根据分形规律可知，每行黑圈与白圈总数为1，3，9，27，…，即和为3n-1。另外每行白圈比黑圈多1个，故黑圈个数为故

点评：本题考查了归纳推理的应用，多观察几组数据是发现规律的有效方法。解法一从黑圈个数的数字规律入手归纳第n行黑圈数；解法二注意到每行黑圈和白圈的总个数，还注意到白圈比黑圈多1个。

变式1某种平面分形图如图3所示，一级分形图是由一点出发的三条线段，长度均为1，两两夹角为120°；二级分形图是在一级分形图的每条线段的末端出发再生成两条长度为原来的线段，且这两条线段与原线段两两夹角为120°，…，依此规律得到n级分形图。

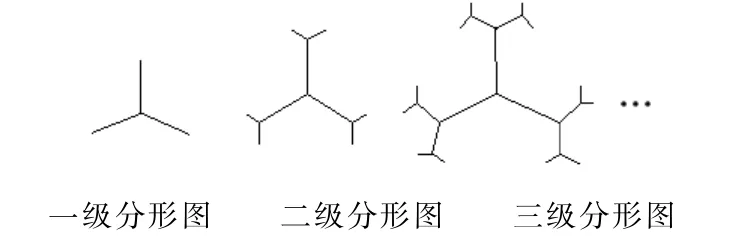
图3

则n级分形图中共有____条线段。

解法一：显然当n=1时有3条线段；

当n=2时，3条线段的另一端各增加2条线段，所以新增3×2条，故此时共有3+3×2条线段；

当n=3时，在n=2时新增的线段的另一端各增加2条线段，所以新增线段(3×2)×2条，故此时共有3+3×2+3×2×2=3(1+2+22)条线段；

……

以此类推，每次都是在上一次的新增线段的另一端各增加2条线段，所以推出n级分形图中有线段3×(1+2+22+…+2n-1)=3(2n-1)条。

解法二：直接看每个图形，每个节点出发有3条线段，数节点即可，但是注意不要数重复了。发现：

一级分形图有1×3=(21-1)×3条；

二级分形图有3×3=(22-1)×3条；

三级分形图有7×3=(23-1)×3条；

……

以此类推，n级分形图中有(2n-1)×3条线段。

二、证明有方法

1.“你中有我，我中有你”的综合法与分析法

实际证题过程中，综合法与分析法往往是结合起来运用的。只是在构建命题的证明路径时，有时分析法占主导地位，综合法伴随其中；有时刚好相反，综合法占主导地位，而分析法伴随其中。

例2若a，b，c是不全相等的正数，求证+l gc。

证明：要证l ga+l gb+l gc，只需证l g(a b c)，即证

点评：此题解题过程中前半部分用的是分析法，后半部分用的是综合法。当然这道题还可以完全按照综合法的形式来证明，只需要把上述证明过程倒过来加以整理即可，在此不再赘述。不管采用分析法还是综合法，单靠一种方法解题显得较为困难。为保证探索方向准确及过程快捷，我们常常要分析中有综合，综合中有分析。

2.“随时待命”的数学归纳法

数学归纳法是用来证明一个与正整数n有关的命题，包括归纳奠基和归纳递推两个步骤。可以用来证明等式、不等式，数列中求通项公式时也可先猜想再用数学归纳法证明。可以说在解这些题时会很明确想到用数学归纳法或者题中明确要求采用数学归纳法。而有些题本身并没有要求用数学归纳法，也不是非用数学归纳法不可的，但是采用了数学归纳法之后题很容易做出来。请看下面例子。

例3已知函数＞0)。

(1)若函数f(x)在[1，+∞)上为增函数，求实数a的取值范围；

(2)当a=1时，求证：对任意大于1的正整数恒成立。

分析：此题的大前提是一个函数，第(1)问根据导数判断单调性即可求解。第(2)问是与正整数n有关的证明题，有两种思路，可以从函数的角度去考虑，也可以用数学归纳法证明。

解：(1)由已知得0)。

a≥对任意x∈[1，+∞)恒成立，而所以a≥1。

(2)证法一：当a=1时，由(1)知f(x)=在[1，+∞)上为增函数，当n＞1，n∈N*时，令则x＞1，所以f(x)＞f(1)=0。

证法二(数学归纳法)：当n=2时，l n2＞，不等式成立。

假设当n=k(k≥2，k∈N*)时，不等式成立，即：

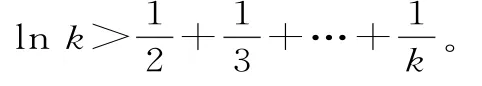
当n=k+1时，l n(k+1)=l nk+

由(1)得x＞1时，f(x)＞f(1)=0，即

综上可知不等式成立。

变式2已知函数(a∈R)。

(1)当a=1时，求f(x)在[1，+∞)上的最小值。

解：(1)当a=1时定义域为(0，+∞)。

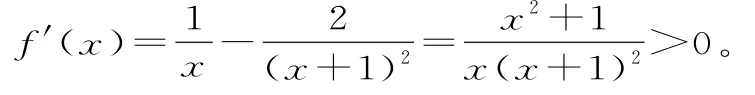
所以f(x)在(0，+∞)上是增函数。

所以f(x)在[1，+∞)内的最小值为f(1)=1。

(2)证法一：根据(1)的结论，当x＞1时，即

证法二(数学归纳法)：当n=1时，l n(n+1)=l n2，因为3 l n2=l n8＞1，所以l n2＞，即当n=1时不等式成立。

假设当n=k(k≥1，k∈N*)时，不等式成立，即：

那么，当n=k+1时，l n(k+2)=l n(k+

由(1)得，当x＞1时，即

故当n=k+1时，不等式也成立。

综上可知不等式成立。