导数压轴题中关于f(x1)-f(x2)取值范围的解决策略

■河南省罗山高级中学 高尤琼

通过研究近几年高考的导数压轴题发现，求f(x1)-f(x2)范围的问题多次出现。笔者通过对此类试题进行研究，发现了题目的共性，总结出解题经验，希望能帮同学们顺利解决此类问题。

例题：(郑州外国语学校月考)设x=m和x=n是函数(a+2)x的两个极值点，其中m＜n，a∈R。

(1)求f(m)+f(n)的取值范围；

解析：

因为x=m和x=n是函数f(x)的两个极值点，所以方程x2-(a+2)x+1=0有两个不等的正根m，n，其中m＜n。

故a＞0，m+n=a+2，m n=1。

因此，f(m)+f(n)=l nm n+1＜-3。

所以f(m)+f(n)的取值范围是(-∞，-3)。

因此，f(n)-f(m)

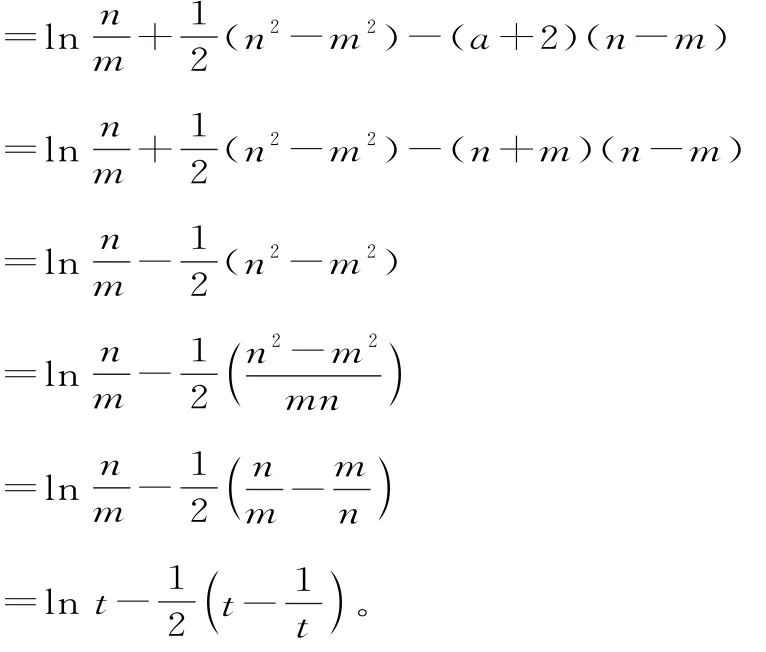
所以g(t)在[e，+∞)上单调递减，g(t)

故f(n)-f(m)的最大值是

因为n＞1，所以

因此，f(n)-f(m)

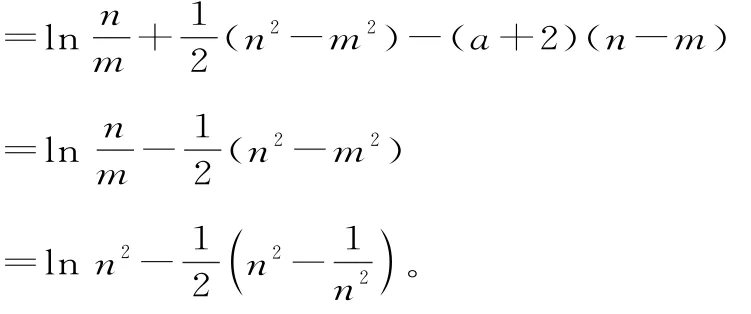
令n2=t，则t≥e，f(n)-f(m)=g(t)

g'(t)=，所以g(t)在[e，+∞)上单调递减

故f(n)-f(m)的最大值是

小结：

(1)函数的定义域为(0，+∞)。因为极值点在定义域内，所以m，n为正数。根据导数中极值点的含义将x=m和x=n代入导函数，再由根与系数的关系得到m，n与参数a的关系式，并得到a的取值范围，进而由参数a的取值范围得出f(m)+f(n)的取值范围。

跟踪练习1.(河北衡水中学2019年调研)已知函数f(x)=al nx-x+1。

(1)若f(x)＜0对任意x∈(1，+∞)恒成立，求实数a的取值范围；

(2)当0＜a≤e+时，若函数g(x)=有两个极值点x1，x2(x1＜x2)，求g(x2)-g(x1)的最大值。

解析：(1)对f(x)=al nx-x+1求导，

当a≤1时，f'(x)＜0，所以f(x)在区间(1，+∞)上单调递减，则有f(x)＜f(1)=0，从而f(x)＜0。

当a＞1时，令f'(x)=0，得x=a。当x∈(1，a)时，f'(x)＞0，则f(x)在区间(1，a)上单调递增，f(x)＞f(1)=0，与f(x)＜0恒成立矛盾，因此不符合题意。

综上，实数a的取值范围为(-∞，1]。

由已知可得g'(x)=0，即关于x的方程-x2+a x-1=0有两个不相等的实数根x1，x2(x1＜x2)，则

故g(x2)-g(x1)

由1＜x≤e，得，故t'(x)＞0。

所以t(x)在(1，e]上单调递增，当x=e时，t(x)取得最大值。

小结：本题用例题的解法2较为简单，利用x1，x2的关系，换掉其中一个变量。

跟踪练习2.(湖南长郡中学2019届高三月考)已知函数f(x)=l nx-a x2在x=1处的切线与直线x-y+1=0垂直。

(1)求函数t(x)=f(x)+x f'(x)(f'(x)为f(x)的导函数)的单调递增区间；

解析：(1)由题意可得并且f'(1)=1-2a=-1，解得a=1。

又因为t(x)=f(x)+x f'(x)=l nx-3x2+1，所以

故t(x)的单调增区间为

(2)g(x)=l n则

因为x1，x2是g(x)的两个极值点，所以x1，x2是方程x2-(1+b)x+1=0的两个根。

由根与系数的关系可知：

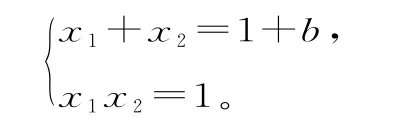
由x1＜x2，可知0＜x1＜1。

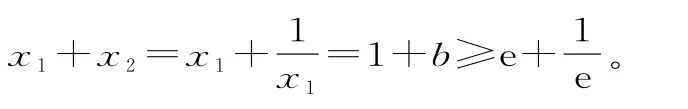
所以g(x1)-g(x2)

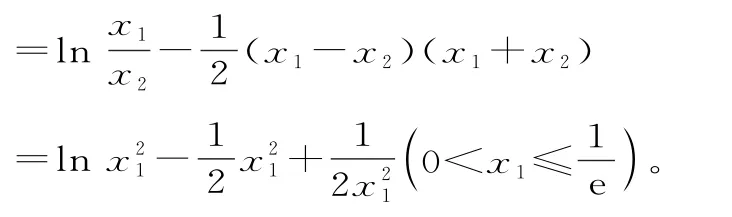
小结：本题用例题中的解法2较为简单，利用x1，x2的关系，换掉其中一个变量。

跟踪练习3.(2017年洛阳市尖子生联考)已知函数f(x)=l nx+m x(m为常数)。

(1)讨论函数f(x)的单调区间；

解析：(1)

①当m＜0时，由1+m x＞0，解得x＜即当时，f'(x)＞0，f(x)单调递增。

由1+m x＜0解得，即当x＞时，f'(x)＜0，f(x)单调递减。

②当m=0时，即f(x)在(0，+∞)上单调递增。

③当m＞0时，1+m x＞0，故f'(x)＞0，f(x)在(0，+∞)上单调递增。

所以，当m＜0时，f(x)的单调递增区间为单调递减区间为当m≥0时，f(x)的单调递增区间为(0，+∞)。

(2)由g(x)=l nx+m x得

已知x2+m x+1=0有两个互异实根x1，x2，故由根与系数的关系得x1+x2=-m，x1x2=1。

因为x1，x2(x1＜x2)是h(x)的两个零点，所以h(x1)=2 l nx1--a x1=0；①

h(x2)=2 l nx2--a x2=0。②

由②-①得：

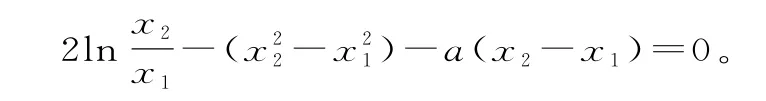
解得

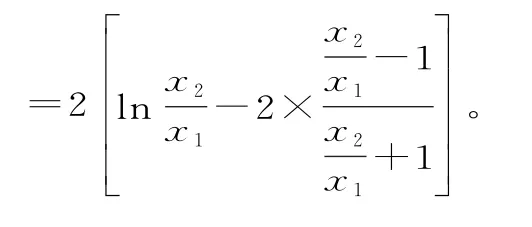
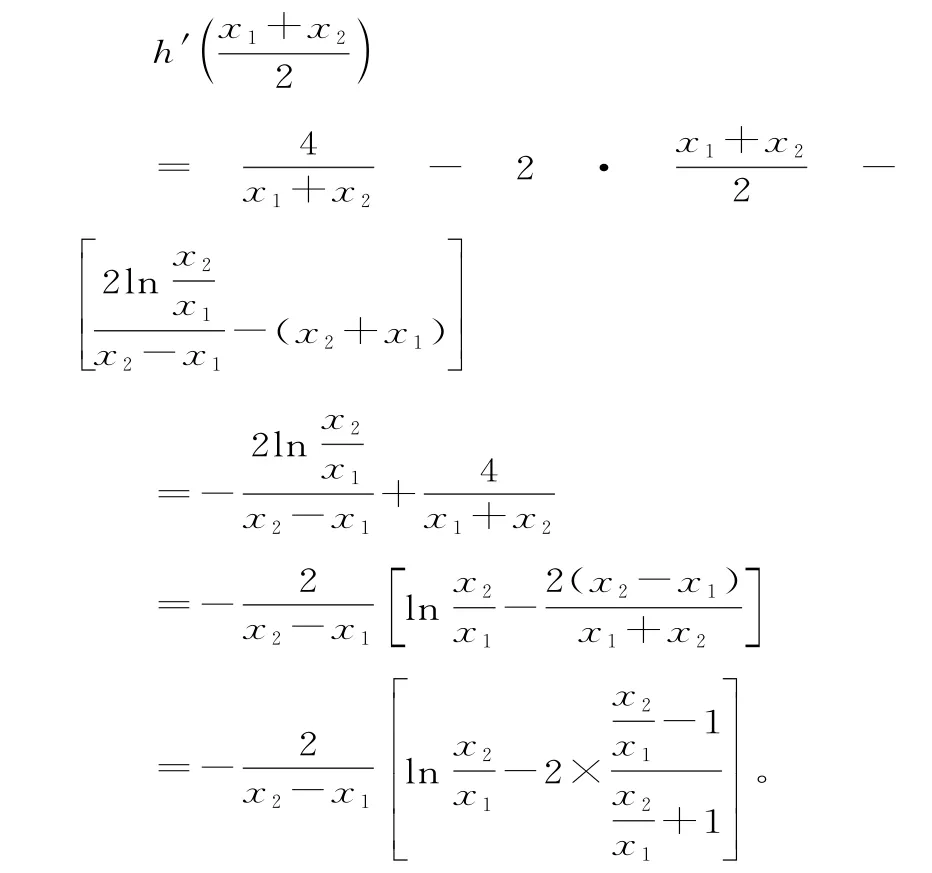
小结：(1)求出函数的导数，通过讨论m的范围，便可求出函数的单调区间。

(2)先求出函数的导数，得到x1+x2=-m，x1x2=1，再求出y=(x1-x2)·的解析式，根据例题的解法1，构造新函数，依据函数的单调性求出其最小值。

跟踪练习4.(2017年河南信阳联考)已知函数

(1)a≥-2时，求F(x)=f(x)-g(x)的单调区间；

(2)设h(x)=f(x)+g(x)，且h(x)有两个极值点为x1，x2，其中，求h(x1)-h(x2)的最小值。

解析：(1)由题意知F(x)=f(x)-，定义域为(0，+∞)。

令m(x)=x2-a x+1=0，有Δ=a2-4。

①当-2≤a≤2时，F'(x)≥0，F(x)的单调增区间为(0，+∞)。

②当a＞2时，F'(x)=0的两根为x1=此时F(x)的单 调 增 区 间 为和F(x)的单调减区间为

综上，当-2≤a≤2时，F(x)的单调增区间为(0，+∞)；当a＞2时，F(x)的单调增区间为F(x)的 单 调 减 区 间 为

(2)由题意知h(x)=f(x)+g(x)=

方程h'(x)=0的两根分别为x1，x2，则有x1·x2=1，x1+x2=-a。

小结：本题用例题中的解法2较为简单，利用x1，x2的关系，换掉其中一个变量。

跟踪练习5.(2017年芜湖模拟卷)已知函数

(1)若a=2，求曲线y=f(x)在点(1，f(1))处的切线l的方程；

(2)设函数g(x)=f'(x)有两个极值点x1，x2，其中x1∈(0，e]，求g(x1)-g(x2)的最小值。

解析：(1)当a=2时，f'(x)=2 l nx+x

f(1)=故切线l的方程为2(x-1)，即4x-2y-3=0。

(2)g(x)=al nx+x-，定义域为，定义域为(0，+∞)。(0，+∞)。

令g'(x)=0，则x2+a x+1=0。

其两根为x1，x2，且x1+x2=-a，x1x2=1，故

则(g(x1)-g(x2))min=h(x)min，h'(x)

当x∈(0，1]时，恒有h'(x)≤0；

当x∈(1，e]时，恒有h'(x)＜0。

总之，h(x)在x∈(0，e]上单调递减。

故(g(x1)-g(x2))min=

小结：(1)求出函数的导数，计算f(1)，f'(1)，便可求出切线方程；