推理与证明综合演练卷

■河南省罗山高级中学 李贵伟

一、选择题

1.下列推理过程是类比推理的是( )。

B.科学家通过研究老鹰的眼睛发明了电子鹰眼

C.通过检测溶液的p H得出溶液的酸碱性

D.由周期函数的定义判断某函数是否为周期函数

2.下列有关三段论推理“自然数都是整数，4是自然数，所以4是整数”的说法正确的是( )。

A.推理正确 B.推理形式不正确

C.大前提错误 D.小前提错误

3.勾股定理：在直角三角形中，直角边长为a，b，斜边长为c，那么a2+b2=c2。类比勾股定理可得：在长、宽、高分别为p、q、r，体对角线长为d的长方体中，有( )。

A.p+q+r=d

B.p2+q2+r2=d2

C.p3+q3+r3=d3

D.p2+q2+r2+p q+p r+q r=d2

4.若a，b，c均为实数，则①a b=b a；②(a b)c=a(b c)；③若a b=b c，b≠0，则a=c；④若a b=0，则a=0或b=0。四个结论均是正确的。

对向量a，b，c，用类比推理可得到以下四个结论：

①a·b=b·a；

②(a·b)c=a(b·c)；

③若a·b=b·c，b≠0，则a=c；

④若a·b=0，则a=0或b=0。

其中结论正确的有( )。

A.0个 B.1个

C.2个 D.3个

5.已 知 数 列｛an｝满 足a1=0，an+1=则a2019等于( )。

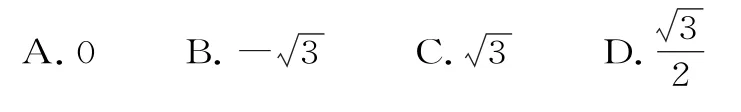
6.由“正三角形的内切圆切于三边的中点”，可类比猜想出正四面体的内切球切于四个侧面( )。

A.各正三角形内任一点

B.各正三角形的某高线上的点

C.各正三角形的中心

D.各正三角形外的某点

7.已知1+2×3+3×32+4×33+…+n×3(n-1)=3n(n a-b)+c对一切n(n为正整数)都成立，那么( )。

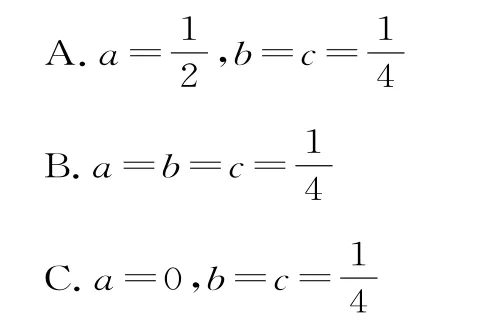
D.不存在这样的a，b，c

8.下列三句话按三段论的模式排列顺序正确的是( )。

①2006能被2整除；

②一切偶数都能被2整除；

③2006是偶数。

A.①②③ B.②①③

C.②③① D.③②①

9.有以下结论：

①已知p3+q3=2，求证：p+q≤2。用反证法证明时，可假设p+q≥2。

②已知|a|+|b|＜1，求证：方程x2+a x+b=0的两根的绝对值都小于1。用反证法证明时，可假设方程有一根x1的绝对值大于或等于1，即假设|x1|≥1。

下列说法中正确的是( )。

A.①与②的假设都错误

B.①与②的假设都正确

C.①的假设正确；②的假设错误

D.①的假设错误；②的假设正确

10.已知f(x)=x3+x，a，b，c∈R，且a+b＞0，a+c＞0，b+c＞0，则f(a)+f(b)+f(c)的值( )。

A.一定大于零 B.一定等于零

C.一定小于零 D.正负都有可能

11.观察1=12，2+3+4=32，3+4+5+6+7=52，…，得出的一般性结论是( )。

A.1+2+…+n=(2n-1)2

B.n+(n+1)+…+(3n-2)=(2n-1)2

C.n+(n+1)+…+(2n-1)=(2n-1)2

D.1+2+…+(3n-2)=(n-1)2

12.若x，y＞0且x+y＞2，则和的值满足( )。

D.不确定

13.已知，依照以上各式的规律，得到一般性的等式为( )。

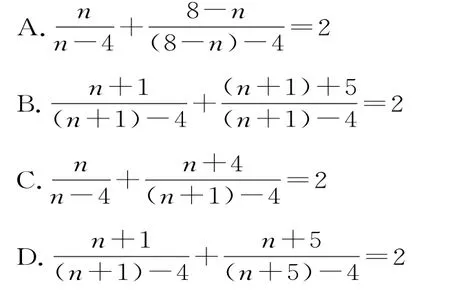
14.已知结论：在正三角形A B C中，若D是边B C的中点，G是三角形A B C的重心，则若把该结论推广到立体几何，则有结论：在棱长都相等的四面体A-B C D中，若△B C D的中心为M，四面体内部一点O到四面体各面的距离都相等，则等于( )。

A.1 B.2 C.3 D.4

15.已知n为正偶数，用数学归纳法证明时，若已假设n=k(k≥2，且k为偶数)时等式成立，则还需利用归纳假设再证( )。

A.n=k+1时等式成立

B.n=k+2时等式成立

C.n=2k+2时等式成立

D.n=2(k+2)时等式成立

16.若a＞b＞c，且为正整数)恒成立，则n的最大值为( )。

A.2 B.3 C.4 D.5

二、填空题

17.在△A B C中，D为边B C的中点，则将上述命题类比到四面体中去，得到一个类比命题：____。

18.对于“求证函数f(x)=-x3在R上是减函数”，用“三段论”可表示为：大前提是“对于定义域为D的函数f(x)，若对任意x1，x2∈D且x1＜x2，有f(x1)＞f(x2)，则函数f(x)在D上是减函数”，小前提是“___”，结论是“f(x)=-x3在R上是减函数”。

19.下面的四个不等式：

①a2+b2+c2≥a b+b c+a c；

②a(1-a)≤

④(a2+b2)·(c2+d2)≥(a c+b d)2。

其中不成立的有____个。

2

0.用数学归纳法证明且为正整数)，第一步要证明的不等式是____。

21.已知x＞0，由不等式，启发我们归纳得到推广结论≥n+1(n为正整数)，其中a的值为____。

三、解答题

22.设f(x)=x2+a x+b，求证：|f(1)|，|f(2)|，|f(3)|中至少有一个不小于

23.已知a＞0，b＞0，a+b=1，求证：

24.观察下表：

1，

2，3

4，5，6，7

8，9，10，11，12，13，14，15，

……

问：(1)此表第n行的最后一个数是多少?

(2)此表第n行的各个数之和是多少?

(3)2008是第几行的第几个数?

25.求 证：为正整数。

26.已知数列｛an｝和｛bn｝的通项公式分别为an=3n+6，bn=2n+7。将集合｛x|x=an｝∪｛x|x=bn｝中的元素从小到大依次排列，构成数列c1，c2，c3，…，cn，…。

(1)写出c1，c2，c3，c4；

(2)求证：在数列｛cn｝中，但不在数列｛bn｝中的项恰为a2，a4，…，a2n，…；

(3)求数列｛cn｝的通项公式。