函数与导数综合演练（A卷）

■河南省罗山高级中学 姜 波

一、选择题

1.设函数f(x)=x3+(a-1)x2+a x，若f(x)为奇函数，则曲线y=f(x)在点(0，0)处的切线方程为( )。

A.y=-2xB.y=-x

C.y=2xD.y=x

2.对于R上可导的任意函数f(x)，若满足则必有( )。

A.f(0)+f(2)＞2f(1)

B.f(0)+f(2)≤2f(1)

C.f(0)+f(2)＜2f(1)

D.f(0)+f(2)≥2f(1)

3.设a为实数，函数f(x)=x3+a x2+(a-3)x的导函数为f'(x)，且f'(x)是偶函数，则曲线y=f(x)在原点处的切线方程为( )。

A.y=3x+1 B.y=-3x

C.y=-3x+1 D.y=3x-3

4.由直线曲线及x轴所围成图形的面积为( )。

5.曲线在点(4，e2)处的切线与坐标轴所围三角形的面积为( )。

6.曲线y=l n(x+2)在点P(-1，0)处的切线方程是( )。

A.y=x+1 B.y=-x+1

C.y=2x+1 D.y=-2x+1

7.由直线y=0与y=s i nx所围成的封闭图形的面积为( )。

8.函数f(x)=x3+b x2+c x+d的大致图像如图1所示，则+等于( )。

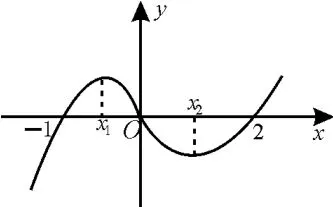
图1

9.曲线在x=0点处的切线方程是( )。

A.x+yl n2-l n2=0

B.xl n2+y-1=0

C.x-y+1=0

D.x+y-1=0

10.如图2，设D是图中边长分别为1和2的矩形区域，E是D内位于函数图像下方的阴影部分区域，则阴影部分E的面积为( )。

A.l n2 B.1-l n2

C.2-l n2 D.1+l n2

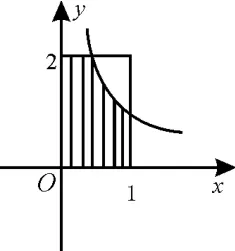
图2

11.已知t＞0，若，则t=( )。

A.1 B.-2 C.-2或4 D.4

12.已知二次函数f(x)=a x2+b x+c的导数为f'(x)，且f'(0)＞0，f(x)的值域为[0，+∞)，则的最小值为( )。

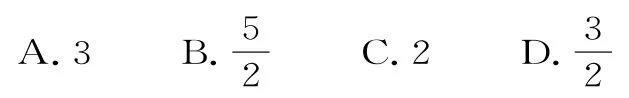
13.已知函数y=f(x)是定义在R上的奇函数，且当x＞0时，f(x)+x f'(x)＞0(其中f'(x)是f(x)的导函数)，设a=，则a，b，c的大小关系是( )。

A.c＞a＞bB.c＞b＞a

C.a＞b＞cD.a＞c＞b

14.我们常用以下方法求形如y=f(x)g(x)的函数的导数：先两边同取自然对数得，l ny=g(x)l nf(x)，再两边同时求导得到f'(x)，于是得到y'=f(x)g(x)[g'(x)·运用此法，可得函数的一个单调递增区间是( )。

A.(e，4) B.(3，6)

C.(0，e) D.(2，3)

15.若a＞0，b＞0，且函数f(x)=4x3-a x2-2b x-2在x=1处有极值，则a b的最大值是( )。

A.2 B.3 C.6 D.9

16.已知函数，则f(π)=( )。

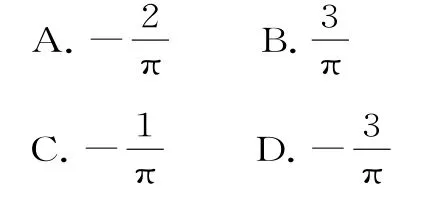
17.函数f(x)的定义域为R，f(-1)=2，对任意x∈R，f'(x)＞2，则f(x)＞2x+4的解集为( )。

A.(-1，1) B.(-1，+∞)

C.(-∞，-1) D.(-∞，+∞)

18.若函数y=e(a-1)x+4x(x∈R)有大于零的极值点，则实数a的取值范围是( )。

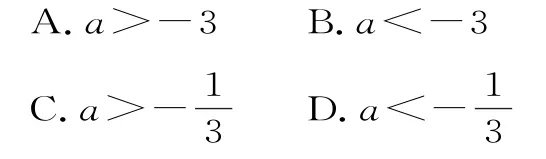
19.若曲线g(x)=xa在点P(1，1)处的切线分别为l1，l2，且l1⊥l2，则a的值为( )。

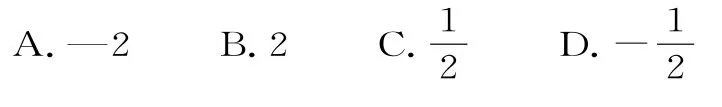
20.函数对任意x1，x2∈(0，+∞)，不等式(k+1)·g(x1)≤k f(x2)(k＞0)恒成立，则实数k的取值范围是( )。

A.[1，+∞) B.[2，+∞)

C.(0，2) D.(0，1]

21.设函数，则y=f(x)( )。

22.已知a＞0，函数f(x)=x3-a x在[1，+∞)上是单调增函数，则a的最大值是( )。

A.0 B.1 C.2 D.3

二、填空题

23.

24.抛物线y=x2在A(1，1)处的切线与y轴及该抛物线所围成的图形面积为____。

25.已知f(x)=xex，g(x)=-(x+1)2+a，若∃x1，x2∈R使得f(x2)≤g(x1)成立，则实数a的取值范围是____。

26.由曲线y=3-x2和直线y=2x所围成的封闭图形的面积为____。

27.已知函数f(x)的导函数为f'(x)，且满足f(x)=2x f'(1)+l nx，则f(x)在点M(1，f(1))处的切线方程为____。

28.已知则常数t=____。

29.设则m与n的大小关系为____。

30.

31.已知函数的图像在点A(x0，y0)处的切线斜率为1，则t a nx0=____。

32.若函数f(x)=x3-3x+a有三个不同的零点，则实数a的取值范围是____。

33.已知函数f(x)的定义域为[-1，5]，部分对应值如表1，f(x)的导函数y=f'(x)的图像如图3所示。

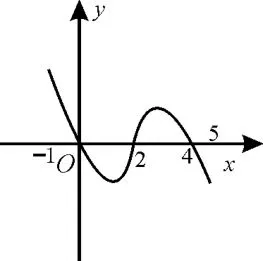
表1

下列关于函数f(x)的命题：

①函数f(x)的值域为[1，2]；

②函数f(x)在[0，2]上是减函数；

③如果当x∈[-1，t]时，f(x)的最大值是2，那么t的最大值为4；

④当1＜a＜2时，函数y=f(x)-a最多有4个零点。

其中正确命题的序号是____。

三、解答题

34.已知f(x)=xl nx-a x，g(x)=-x2-2，

(1)对一切x∈(0，+∞)，f(x)≥g(x)恒成立，求实数a的取值范围；

(2)当a=-1时，求函数f(x)在[m，m+3](m＞0)上的最值；

(3)证明：对一切x∈(0，+∞)，都有l nx成立。

35.已知函数

(1)若曲线y=f(x)在点P(1，f(1))处的切线与直线y=x+2垂直，求函数y=f(x)的单调区间；

(2)若对于∀x∈(0，+∞)都有f(x)＞2(a-1)成立，试求a的取值范围；

(3)记g(x)=f(x)+x-b(b∈R)，当a=1时，函数g(x)在区间[e-1，e]上有两个零点，求实数b的取值范围。

36.函数f(x)=l nx+(x-a)2，a∈R。

(1)若a=0，求函数f(x)在[1，e]上的最小值；

(2)若函数f(x)在上存在单调递增区间，试求实数a的取值范围；

(3)求函数f(x)的极值点。