复数中创新问题的探究

■河南省罗山高中老校区 潘载香

数学创新题是训练和考查同学们的数学思维能力、分析问题和解决问题的能力的好题型。现就复数中的创新问题加以盘点，以期能对大家的学习有所启发。

一、新定义型

新定义创新题是近几年出现的新题型，此类题背景新颖、构思巧妙，能有效地甄别同学们的思维品质和学习潜力。

例1定义一种运算如下x1y2-x2y1，复数是虚数单位)的共轭复数是( )。

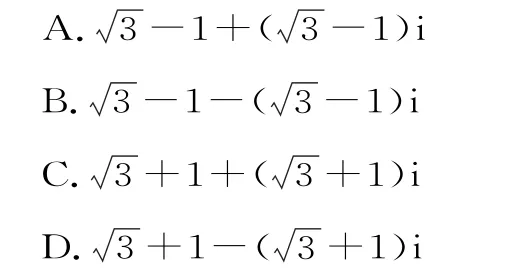
解析：故z的共轭复数为故选B。

点评：本题新定义了一种运算结构，根据新定义的运算结构求出z，从而将问题顺利解决。

例2对任意一个复数z定义集合Mz={ω|ω=z2n-1，n∈N*}，设z满足z4-1=0，则集合Mz的子集的个数可能为____。

分析：通过对相应方程的求解，求出相应的根后再根据对应的定义加以分析与判断。

解析：由z4-1=0得，z=±i或者z=±1，由于ω=z2n-1，n∈N*，对应代入可知集合Mz中元素有1个或2个，即Mz的子集的个数可能为2个或4个。

点评：解决此类问题，有时也可以通过特殊值，结合相关等式的幂指数的周期性加以分析求解。通过相应的关系式，根据集合中元素互异性，对相应的复数问题加以综合剖析。

二、结论开放型

例3复数z=a+bi，a，b∈R，且b≠0，若z2-4b z是实数，则有序实数对(a，b)可以是____。(写出一个有序实数对即可)

解析：因为z2-4b z=(a+bi)2-4b(a+bi)=(a2-4a b-b2)+(2a b-4b2)i∈R，所以2a b-4b2=0，a=2b，故可填(2，1)。

点评：结论开放型创新问题，结论是不确定或不唯一的，解题时要注意运用相应的解题策略。本题结论开放，可以写出无数个实数对，如(4，2)，(8，4)等，只要满足a=2b即可。解决此类问题的关键是熟练掌握复数及相关概念。

例4已知a，b，c，d∈R，对于复数z=a+bi，有z(4-i)是纯虚数，(z+2)(1-4 i)是实数，且函数f(x)=a x3+b x2+c x+d在x=0处有极值-2。

(1)求f(x)的单调区间。

(2)是否存在整数m，使得方程f(x)=0在区间(m，m+1)内有且仅有一个实数根?若存在，求出所有m的值；若不存在，请说明理由。

解析：(1)因为z(4-i)=(4a+b)+(-a+4b)i∈{纯虚数}，(z+2)(1-4 i)=(a+4b+2)-(4a-b+8)i∈R，且a，b∈R，所以有：

结论开放型创新题主要有两种类型：一类是给出多个问题确定出若干个正确(或错误)的结论；一类是结论有无数个只需确定出一个正确的结论。

又因为f(x)在x=0处有极值-2，故f'(0)=0，f(0)=-2，得c=0，d=-2。

故f(x)=-x3+4x2-2，则f'(x)=或故f(x)的单调递增区间是，单调递减区间是(-∞，0)和

(2)由(1)知，当x=0时，f(x)有极小值-2＜0。

故方程f(x)=0在f(x)的三个单调区间(-∞，0)上必各有且仅有一个根。

因为f(1)=1＞0，f(0)＜0，所以方程f(x)=0在(0，1)上有且仅有一个实数根。同理可得方程f(x)=0在(3，4)，(-1，0)上有且仅有一个实数根。则m的值为0，3或-1。

点评：本题是一道复数与导数的交汇问题，考查了复数的概念，导数的应用及函数零点的判断方法，综合性较强。解决此类问题常见的方法为：直接法、分析法、反证法，本题运用的是直接法，即直接根据题设条件及所学知识进行推理，以确定问题是否存在。

三、与其他知识交汇型

复数的考查往往与其他知识相结合，复数在其他的知识背景下，有确定的几何意义和现实背景，这类问题往往出题很灵活。

例5已知关于x的方程：x2-(6+i)·x+9+ai=0(a∈R)有实数根b。

(1)求实数a，b的值；

(2)若复数z满足0，求z为何值时，|z|有最小值，并求出此值。

分析：(1)根据b是方程的实根入手，结合两个复数相等的充要条件(特别是其中一个复数为零)，列方程求解出对应的参数；(2)通过设出所求的复数z=x+yi(x，y∈R)，根据复数模的定义得到复数z对应的点Z(x，y)满足的轨迹方程，再结合点Z(x，y)轨迹的图像求出相应的最值。

解析：(1)因为b是方程x2-(6+i)x+9+ai=0(a∈R)的实根，所以(b2-6b+9)+(a-b)i=0，故解得a=b=3。

(2)设z=x+yi(x，y∈R)，由|-abi|=2|z|，得(x-3)2+(y+3)2=4(x2+y2)，即(x+1)2+(y-1)2=8，Z点的轨迹是以O1(-1，1)为圆心为半径的圆。结合图像，当Z点在O O1的边线上时，|z|有最大值或最小值。因为半径r=所以当z=1-i时

点评：以复数为背景知识，结合轨迹问题来解决相关的解析几何问题，一般以圆的内容居多，同时考查数形结合能力、知识的综合运用与转化能力。

例6对于任意两个复数z1=x1+y1i，z2=x2+y2i(x1，y1，x2，y2∈R)，定义运算“☉”为：z1☉z2=x1x2+y1y2，设非零复数ω1，ω2在复平面内对应的点分别为P1，P2，点O为坐标原点，如果ω1☉ω2=0，那么在△P1O P2中，∠P1O P2的大小为____。

分析：结合新定义，设出对应的复数ω1，ω2，结合关系式与对应的边长来判断三角形三边关系，从而判定对应的角的大小。

解析：设ω1=a1+b1i，z2=a2+b2i(a1，b1，a2，b2∈R)，由ω1☉ω2=0，得a1a2+b1b2=0。

又|O P1|2=+，|O P2|2=+，|P1P2|2=(a1-a2)2+(b1-b2)2，所以|O P1|2+|O P2|2=|P1P2|2，根据勾股定理可知∠P1O P2=90°，故答案为90°。

点评：本题充分利用新定义，把复数与新定义的运算综合，考查复数、平面几何等相关的知识，以新定义创新，达到复数与相关知识综合的目的。

由于目前对复数考查多以中低档题目出现，难度不大，但涉及面较广，有的题目还具有一定的综合性和创新性，所以，同学们解决该部分问题的关键是正确把握复数的概念这个理论基础，准确进行复数的四则运算，巧妙应用复数的几何意义。