2018年全国卷Ⅰ理科解析几何第19题的解析和探究

广东 郑灿基

1.试题

2018年高考全国卷Ⅰ理科第19题试题如下：

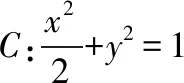
(1)当l与x轴垂直时，求直线AM的方程；

(2)设O为坐标原点，证明：∠OMA=∠OMB.

本题立意新颖，内涵丰富，考查了直线的方程、斜率、直线与椭圆的位置关系、韦达定理、两角相等的等价转化处理，是一道综合性较强的试题.试题分为两问，层次明显，第一问注重基础，难度较小；第二问有一定的难度，重点检测学生的运算求解能力、推理论证能力等，突出对数学核心素养的考查.以下着重讨论第二问的解法.

2.解法呈现

【思路1】证明两直线的斜率之和为零.

证法1：当l与x轴重合时，∠OMA=∠OMB=0°.

当l与x轴垂直时，OM为AB的垂直平分线，所以∠OMA=∠OMB.

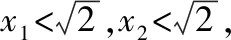
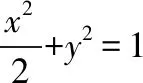
综上，∠OMA=∠OMB.

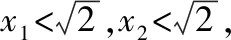
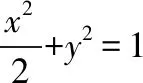
【思路2】利用对称性，证明三点共线.

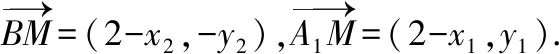
【思路3】到角两边距离相等的点在角平分线上.

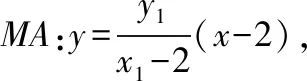
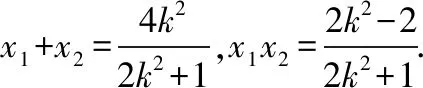
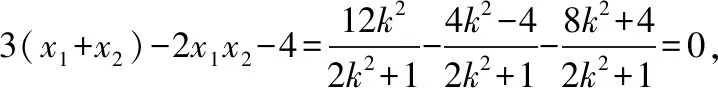
【思路4】利用角平分线定理和直线的参数方程

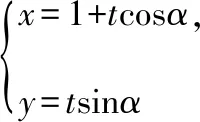
设A(1+t1cosα,t1sinα)，B(1+t2cosα,t2sinα),M(2,0)，

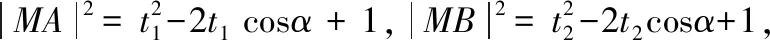
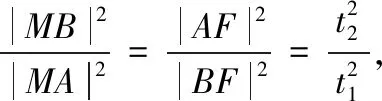
【思路5】利用相似三角形进行转化.

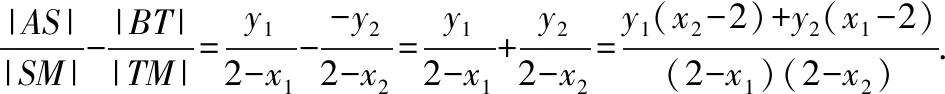
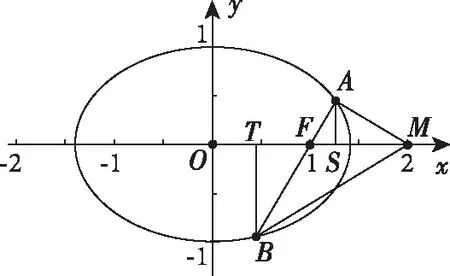
【思路6】利用椭圆的第二定义和平面几何知识解决

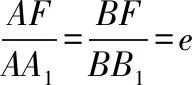
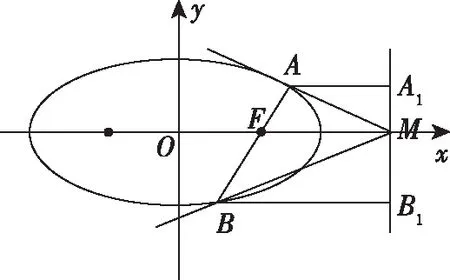
需要指出的是，思路1的两种证法都是将几何问题转化为代数运算，不同的是直线方程的假设形式.证法1是常规算法，即用点斜式法设直线方程为y=k(x-1)，带来的结果是在①中多处出现参数k和k2，运算较为繁琐，且不完备(不包含斜率不存在的情形).而证法2是把直线设为x=my+1，把x看作y的函数，求解过程较为简单，得到的②式中含m的频数少，而且完备性好，包括了满足所有条件的直线方程.同时，在接下来的运算中较为简洁.因此，根据题设条件特点，选用恰当的直线和圆锥曲线方程是强化求简、降低计算的重要手段.一般而言，若直线过的点是(0,t),我们常把直线假设为y=kx+t(假设斜率存在)，而若直线过的点是(t,0),我们常假设直线的方程为x=my+t，这样可以高效解题.

3.引申探究

3.1显性结论

本题中第二问实质上揭示了椭圆的一个性质：椭圆C的准线与长轴的交点M和过相应的焦点F的弦的两端点A,B连线所成角∠AMB被长轴平分.在双曲线、抛物线中也有类似的性质：

①双曲线C的准线与实轴的交点M和过相应的焦点F的弦的两端点A,B连线所成角∠AMB被实轴平分.

②抛物线C的准线与对称轴的交点M和过相应的焦点F的弦的两端点A,B连线所成角∠AMB被对称轴平分.

其证明仿照上面高考题的证法，过程略.以上结论可以统一为：

定理1：圆锥曲线准线与长轴(或实轴、或对称轴)的交点M和相应的焦点弦端点A,B连线所成的角∠AMB被长轴(或实轴、或对称轴)平分.

3.2隐性结论

上面结论中AB是圆锥曲线过焦点的弦,M点是圆锥曲线准线与对称轴的交点，如果AB是圆锥曲线中任意一条弦，点M是与对称轴垂直的直线与该对称轴的交点，那么圆锥曲线是否也有类似的性质呢？

利用《几何画板》实验，笔者发现如下性质：

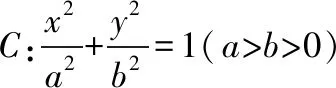
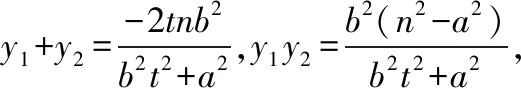
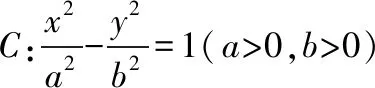
③已知抛物线C:y2=2px(p>0)和x轴上的两点M,N(xN>0)，过点N引直线交抛物线C于A,B两点，则∠AMN=∠BMN⟺xM=-xN.

性质②和③的证明类似性质①，故省略.

以上性质可统一为：

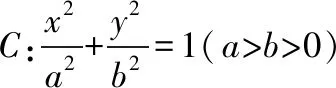
3.3进一步研究

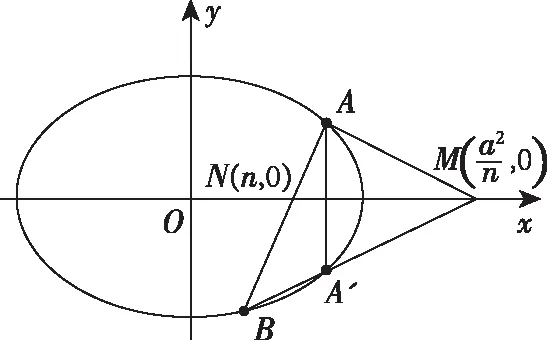
以此类推，不难得到如下结论：

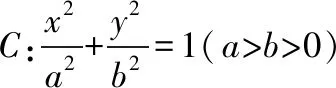
过抛物线C:y2=2px(p>0)的对称轴上的一点N(n,0)(n>0)作弦AB，点A(或点B)关于x轴的对称点为A′(或B′)，则点A′,B,M(-n,0)(或A,B′,M(-n,0))三点共线.

3.4条件与结论互换

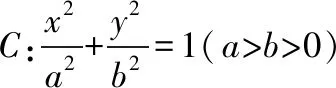
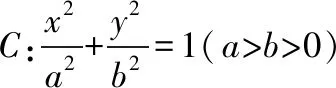
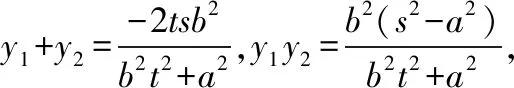
4.结束语