高考导数压轴题中“怪数”的前生——函数零点所在区间端点值选取的定量探究

辽宁 张 军

从近几年高考试题来看，函数零点个数问题一直是高考压轴题的热门考点.不论是讨论零点的个数，还是给定零点的个数求参量的取值范围，解题时利用函数的单调性和极限知识，结合函数图象进行判断并不是很难，但如果要从代数角度进行论证，就需要利用函数的单调性和零点存在性定理来解决.单调性往往容易判断、证明，但想找到一个满足条件的函数值或正负交替的区间端点值特别困难.仔细观察高考试题的答案，感觉答案中给出的数像是横空出世，不知从何而来，那么高考题答案中的“怪数”是怎么来的呢？下面对近四年高考试题的答案加以分析，探索寻找零点所在区间端点的一般规律和方法.

【必备知识】

1.函数的零点存在性定理：如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线，并且有f(a)·f(b)<0，那么函数y=f(x)在区间(a,b)内有零点，即存在c∈(a,b)，使得f(c)=0，这个c也就是方程f(x)=0的根.

2.推论：如果函数y=f(x)在区间[a,b]上的图象是一条连续不断且单调递增(或单调递减)的曲线，并且有f(a)·f(b)<0，那么函数y=f(x)在区间(a,b)内有且只有一个零点.

【例题选讲】

方法一：逐一放缩，取交集.

例1.(2015·全国卷Ⅰ文·21)设函数f(x)=e2x-alnx.

(Ⅰ)讨论f(x)的导函数f′(x)的零点的个数；

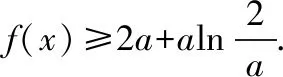
高考答案：(Ⅰ)f(x)的定义域为(0,+∞),

当a≤0时，f′(x)>0，f′(x)没有零点；

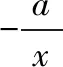
所以f′(x)在(0,+∞)上单调递增，又f′(a)=2e2a-1>0，

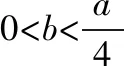
(Ⅱ)证明：由(Ⅰ)知，可设f′(x)在(0,+∞)上的唯一零点为x0，当x∈(0，x0)时，f′(x)<0；

当x∈(x0，+∞)时，f′(x)>0.

故f(x)在(0，x0)上单调递减，在(x0，+∞)上单调递增，所以x=x0时，f(x)取得最小值，最小值为f(x0).

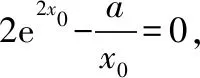
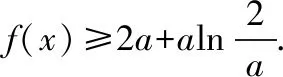
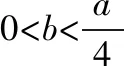
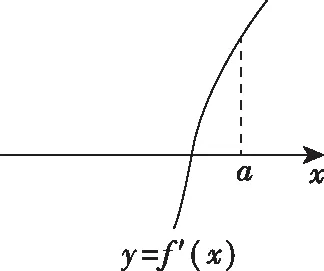
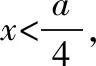
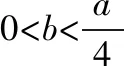
例2.(2018·全国卷Ⅲ理·21)已知函数f(x)=(2+x+ax2)ln(1+x)-2x．

(Ⅰ)若a=0，证明：当-10时，f(x)>0；

(Ⅱ)若x=0是f(x)的极大值点，求a．

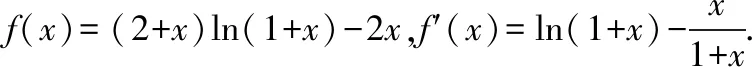
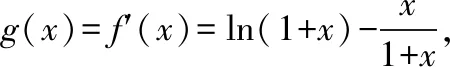
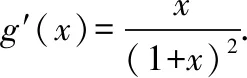
当-10时，g′(x)>0．故当x>-1时，g(x)≥g(0)=0，且仅当x=0时，g(x)=0，从而f′(x)≥0，且仅当x=0时，f′(x)=0．

所以f(x)在(-1，+∞)上单调递增．

又f(0)=0，故当-10时，f(x)>0．

(Ⅱ)(i)若a≥0，由(Ⅰ)知，当x>0时，f(x)≥(2+x)·ln(1+x)-2x>0=f(0)，这与x=0是f(x)的极大值点矛盾．

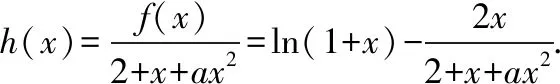
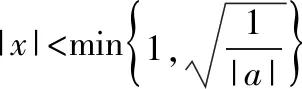
又h(0)=f(0)=0，故x=0是f(x)的极大值点当且仅当x=0是h(x)的极大值点．

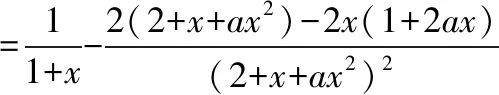
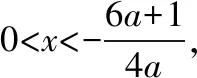
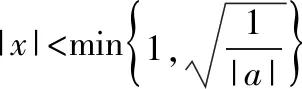
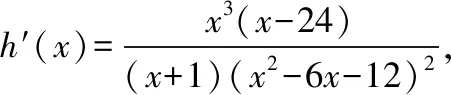
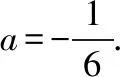
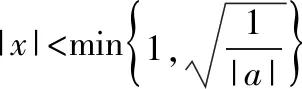
思路分析：需要说明f(x)与h(x)在“0”附近小区间内的函数值符号相同，在这个小区间内既要满足函数f(x)的定义域x∈(-1,+∞)，又要满足2+x+ax2>0恒成立，故可在x>-1的基础上，先对“2+x+ax2”中的一次项“x”进行放缩，再解含参不等式1+ax2>0，二者取交集就可以了.

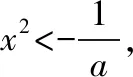
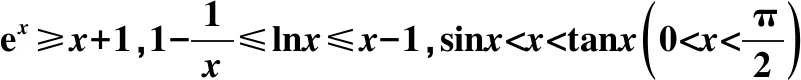
例3.(2017·全国卷Ⅰ理·21)已知函数f(x)=ae2x+(a-2)ex-x.

(Ⅰ)讨论f(x)的单调性；

(Ⅱ)若f(x)有两个零点，求a的取值范围.

高考答案：(Ⅰ)f(x)的定义域为(-∞,+∞)，f′(x)=2ae2x+(a-2)ex-1=(aex-1)(2ex+1).

(i)若a≤0，则f′(x)<0，所以f(x)在(-∞,+∞)上单调递减.

(ii)若a>0，则由f′(x)=0，得x=-lna.

当x∈(-∞,-lna)时，f′(x)<0；当x∈(-lna,+∞)时，f′(x)>0.

所以f(x)在(-∞,-lna)上单调递减，在(-lna,+∞)上单调递增.

(Ⅱ)(i)若a≤0,由(Ⅰ)知f(x)至多有一个零点.

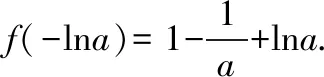
①当a=1时，由于f(-lna)=0，故f(x)只有一个零点；

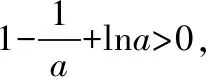
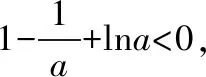
又f(-2)=ae-4+(a-2)e-2+2>-2e-2+2>0，故f(x)在(-∞,-lna)上有一个零点.

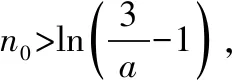
则f(n0)=en0(aen0+a-2)-n0>en0-n0>2n0-n0>0.

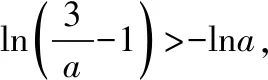
综上，a的取值范围为(0,1).

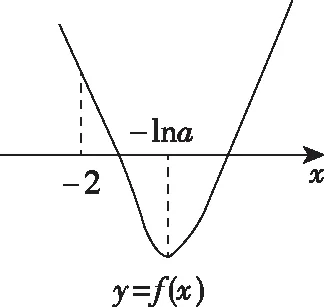
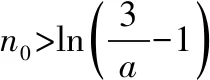
思路分析：想要求解不等式ae2x+(a-2)ex-x>0非常困难，故可考虑利用学过的不等式“ex≥x+1>x”将“x”放缩为“ex”，进而解指数不等式就可以了.

难点突破：ae2x+(a-2)ex-x>0，因为ex≥x+1>x，所以a·e2x+(a-2)·ex-x>a·e2x+(a-2)·ex-ex.

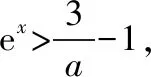
方法三：利用局部函数的最值进行放缩

例4.(2016·全国卷Ⅰ理·21)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.

(Ⅰ)求a的取值范围；

(Ⅱ)设x1，x2是f(x)的两个零点，证明：x1+x2<2.

高考答案：(Ⅰ)f′(x)=(x-1)ex+2a(x-1)=(x-1)·(ex+2a)．

(i)设a=0，则f(x)=(x-2)ex，f(x)只有一个零点．

(ii)设a>0，则当x∈(-∞,1)时，f′(x)<0；当x∈(1,+∞)时，f′(x)>0．所以f(x)在(-∞,1)上单调递减，在(1,+∞)上单调递增．

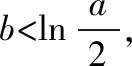
(iii)设a<0，由f′(x)=0得x=1或x=ln(-2a)．

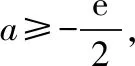
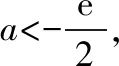
又当x≤1时，f(x)<0，所以f(x)不存在两个零点．综上，a的取值范围为(0,+∞)．

(Ⅱ)证明：不妨设x1f(2-x2)，即f(2-x2)<0．

由于f(2-x2)=-x2e2-x2+a(x2-1)2，而f(x2)=(x2-2)ex2+a(x2-1)2=0，所以f(2-x2)=-x2e2-x2-(x2-2)ex2．

设g(x)=-xe2-x-(x-2)ex，则g′(x)=(x-1)(e2-x-ex)．

所以当x>1时，g′(x)<0，而g(1)=0，故当x>1时，g(x)<0．

从而g(x2)=f(2-x2)<0，故x1+x2<2．

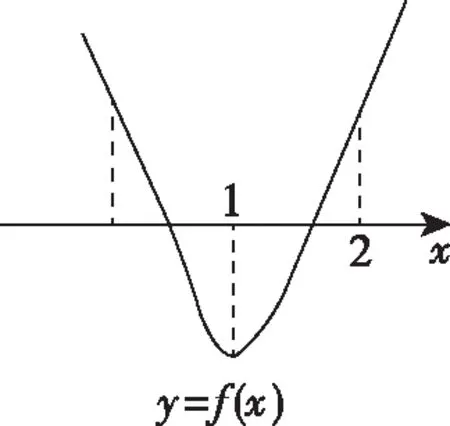
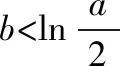
思路分析：因为函数f(x)的解析式涉及了基本初等函数的乘除运算，所以想要求解不等式(x-2)·ex+a(x-1)2>0非常困难.故可以考虑先将函数f(x)的形式转化为两个基本初等函数的加减运算，然后求解一个基本初等函数的值域，根据最值进行放缩之后，再解和另一个函数相关的不等式就可以了.