巧处理，活变形，突破高考统计大题的运算瓶颈

广东 林国红

近年来，高考对数学能力的考查强调“以能力立意”，强调综合性、应用性，并要求切合考生的实际.在高考试卷中，能综合考查学生的运算求解能力和数据处理能力的，无疑是统计大题了.统计大题一般有文字阅读量较大、数据的信息点多、计算量偏大的特点.而近几年统计解答题的得分都不尽如人意，其原因之一是学生在解题时停留在直接套用公式计算上，不会对计算公式进行变形与数据的处理，又多因运算能力不足，导致计算困难，信心受挫，解题过程一旦受阻，无法找到解题方向及时调整思路，则会在“思路单一，运算难行”的兴叹中无奈放弃.

下面笔者以几道统计题为例，对解题中的数据处理技巧、公式变形应用等方面加以分析说明，希望能抛砖引玉，以此增强高三复习的针对性，突破高考统计大题的运算瓶颈.

一、数据的巧处理

例1(2011·安徽卷文·20)某地最近十年粮食需求量逐年上升，下表是部分统计数据：

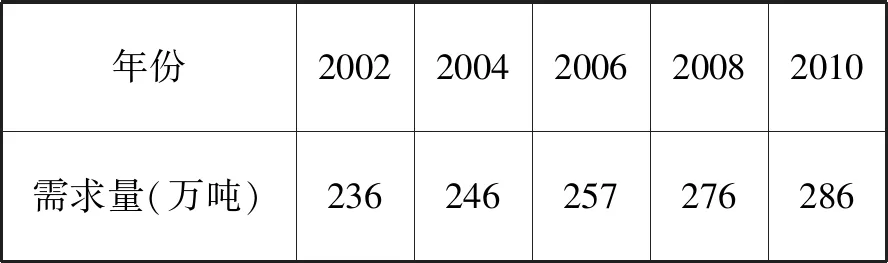
年份20022004200620082010需求量(万吨)236246257276286

(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该地2012年的粮食需求量.

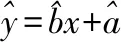
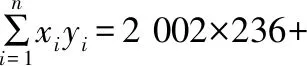
解答：(Ⅰ)由所给数据得出，年需求量与年份之间是近似直线上升的关系，下面来配回归直线方程，为此对数据处理如下：

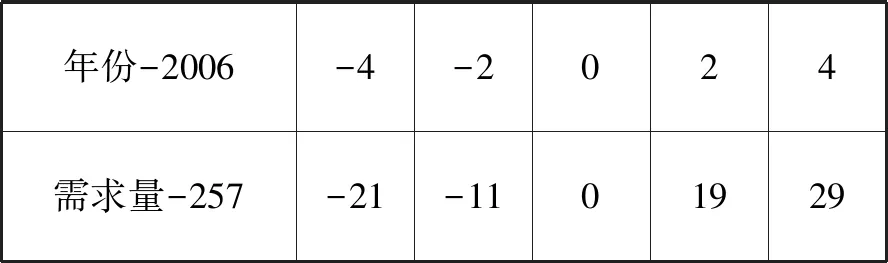
年份-2006-4-2024需求量-257-21-1101929

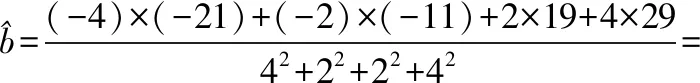
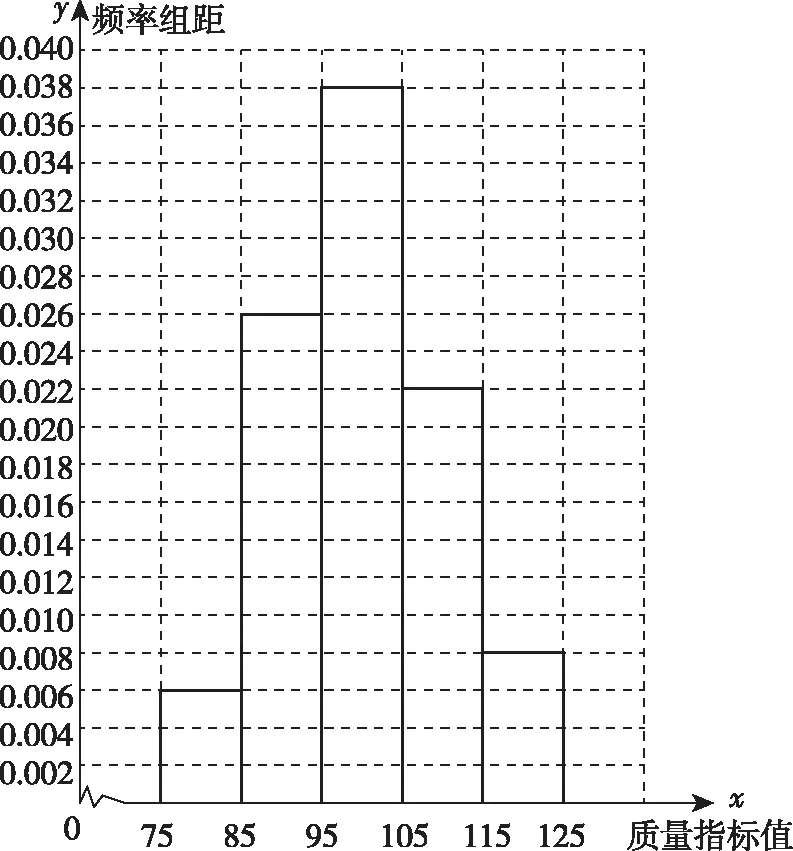
例2从某企业生产的产品的生产线上随机抽取200件产品，测量这批产品的一项质量指标值，由测量结果得如图所示的频率分布直方图：

(Ⅱ)若该种产品的等级及相应等级产品的利润(每件)参照以下规则(其中Z为产品质量指标值)：

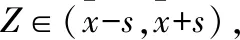
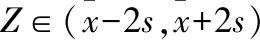
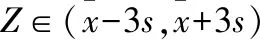
否则该产品定为不合格品，企业将损失1 000元.

(i)若测得一箱产品(5件)的质量指标数据分别为：76，85，93，105，112，求该箱产品的利润；

分析：①本题的“题源”是2014年全国乙卷文科第18题，高考题的数据及问题与本题的第一个问题完全一样(值得注意的是：2014年高考题也是“2018年考试大纲文科说明”的示例)；

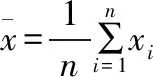
③其实题目已给出相应的说明：“同一组中的数据用该组区间的中点值代表”，这表明同一组中的所有数据都是同一个值 ，如第一组[75,85)中的所有产品质量指标值均是80，而且由题目可以得到每组的频率与频数，这样样本的平均数与方差就可以求了.

解答思路：由题意，可得第一组[75,85)的产品频数为200×0.006×10=12，设这12件产品的产品质量指标值为x1,x2,…,x12，则有x1=x2=…=x12=80.其他组同理可得，数据分组如下表：

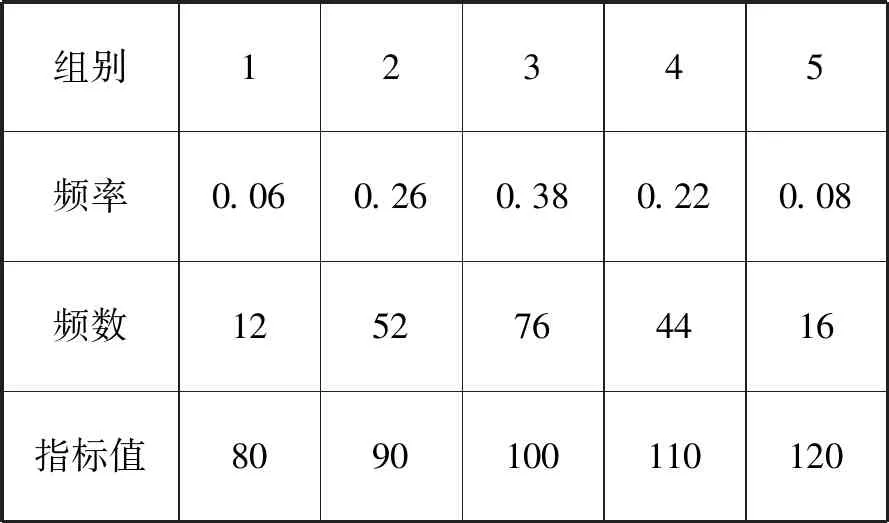
组别12345频率0.060.260.380.220.08频数1252764416指标值8090100110120

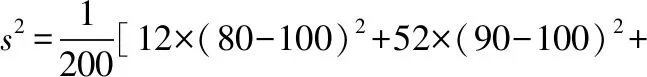
可以看出，实质上由指标值与相应的频率就可算得平均值与方差.

解答：(Ⅰ)产品质量指标值的样本平均数为：

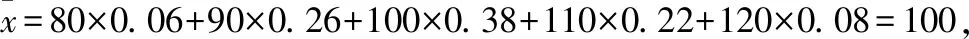
产品质量指标值的样本方差为：

s2=0.06×(-20)2+0.26×(-10)2+0.38×02+0.22×102+0.08×202=104.

(Ⅱ)略.

二、公式的灵活变形

例3(2016·全国卷Ⅲ文·18)下图是我国2008年至2014年生活垃圾无害化处理量(单位：亿吨)的折线图.

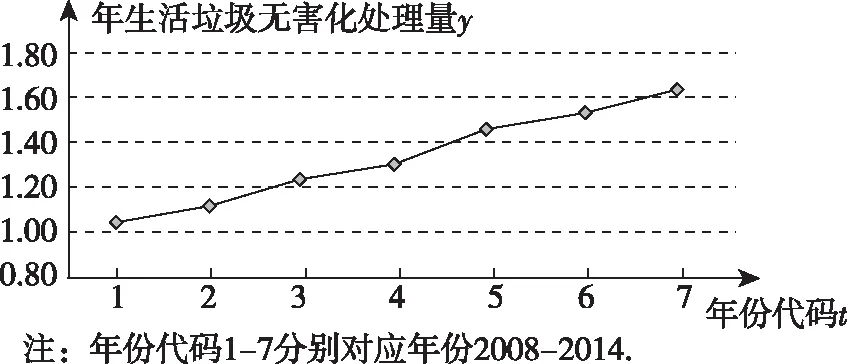
(Ⅰ)由折线图看出，可用线性回归模型拟合y与t的关系，请用相关系数加以说明；

(Ⅱ)建立y关于t的回归方程(系数精确到0.01)，预测2016年我国生活垃圾无害化处理量.

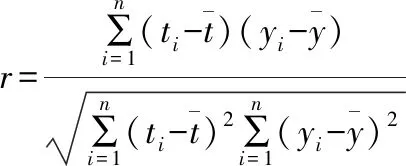
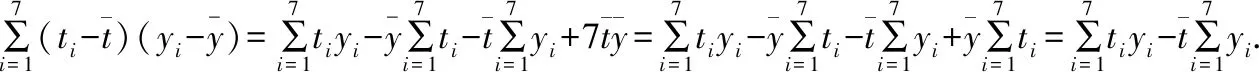
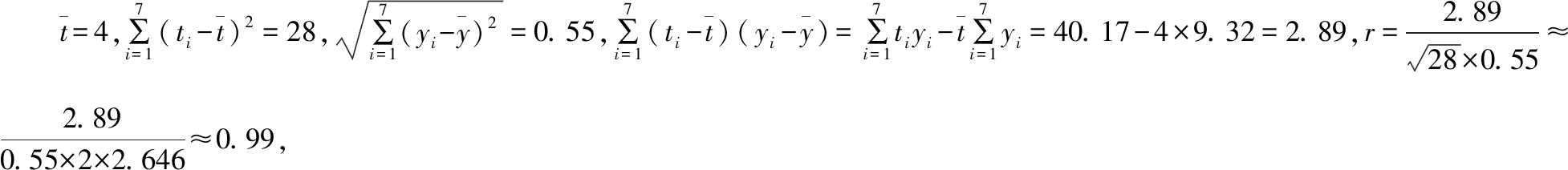
因为y与t的相关系数近似为0.99，说明y与t的线性相关程度相当高，从而可以用线性回归模型拟合y与t的关系.

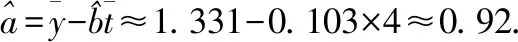
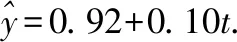
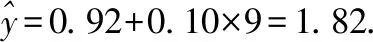
所以预测2016年我国生活垃圾无害化处理量将约为1.82亿吨.

例4(2017·全国卷Ⅰ文·19)为了监控某种零件的一条生产线的生产过程，检验员每隔30 min从该生产线上随机抽取一个零件，并测量其尺寸(单位：cm).下面是检验员在一天内依次抽取的16个零件的尺寸：

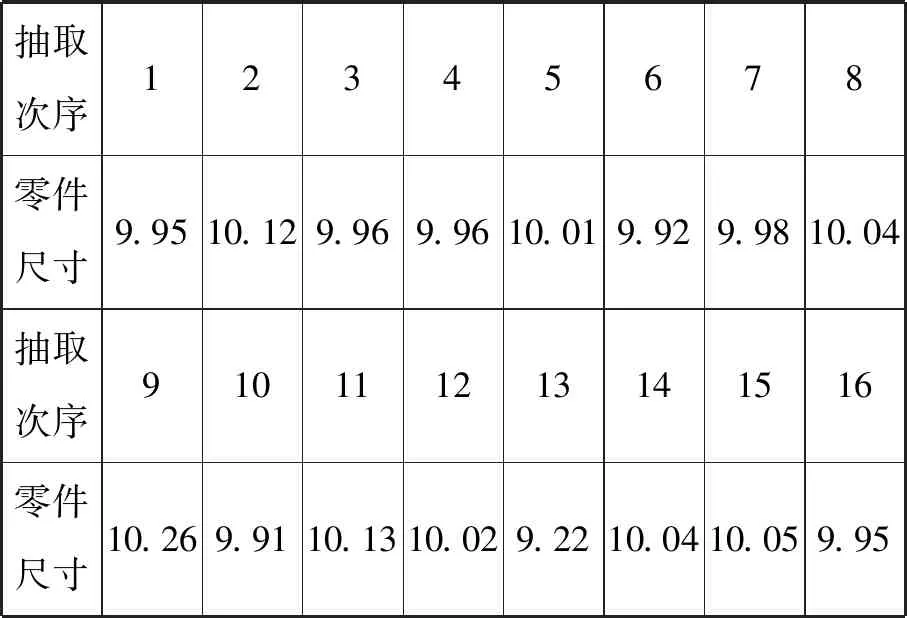
抽取次序12345678零件尺寸9.9510.129.969.9610.019.929.9810.04抽取次序910111213141516零件尺寸10.269.9110.1310.029.2210.0410.059.95

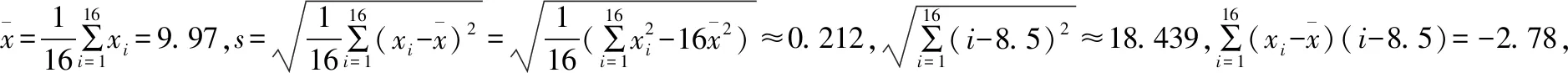
(Ⅰ)求(xi,i)(i=1,2,…,16)的相关系数r，并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小(若|r|<0.25，则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小).

(ⅰ)从这一天抽检的结果看，是否需对当天的生产过程进行检查？

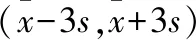
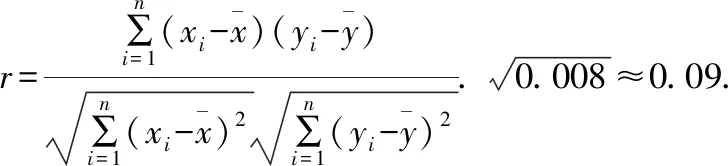
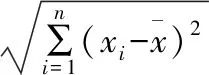
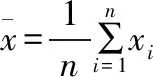
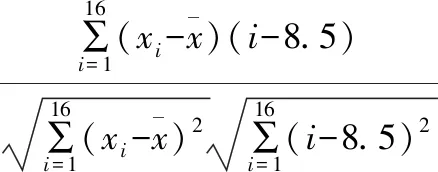
≈-0.18，

由于|r|<0.25，则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小.

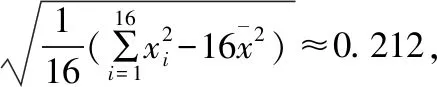
剔除第13个数据，剩下数据的样本方差为

三、小结反思

1.教师要清楚考纲的要求

2018年版《普通高等学校招生全国统一考试大纲》的“考核目标与要求”中对能力的要求有七点，包括空间想象能力、抽象概括能力、推理论证能力、运算求解能力、数据处理能力以及应用意识和创新意识.其中“数据处理能力”是指：会收集、整理、分析数据，能从大量数据中抽取对研究问题有用的信息，并做出判断.选择合适的统计方法整理数据，并构建模型对数据进行分析、推断，获得结论.“运算求解能力”是指：会根据法则、公式进行正确运算、变形、和数据处理，能根据问题的条件寻找合理、简捷的运算途径，能根据要求对数据进行估计和近似计算.运算能力包括分析运算条件、探究运算方向、选择运算公式、确定运算程序等一系列过程中的思维能力，也包括在实施运算过程中遇到障碍而调整运算的能力.

教师只有在吃透考纲的前提下，才能做到有的放矢，高三的复习才有针对性，要结合考纲的要求，进行相应的训练，才可能提高复习的有效性.

2.教学建议