创设恰当问题情境，引领课堂高效生成

甘肃 张建文

问题是驱动课堂前进的催化剂，合理而巧妙的设置问题对教学效果的提高起着至关重要的作用.本文针对习题讲解过程中不同的习题类型创设不同的问题作一简要说明.

1.创设问题的含义：学生与老师提出的问题之间形成一种这样的情境——具有一定概括性或点拨性的问题与学生已有的认知结构之间产生矛盾冲突,虽然凭现有的知识和技能解决起来比较困难,但学生思考的空间比较大，这样学生的求知欲望被激发起来.在教师的帮助点拨下，经过分析问题、探索并提出解决问题的方法、检验这种方法是否有效等思维活动达到掌握知识解决问题的目的.

常见的课堂提问有以下三种类型：

1.1检测性提问：设置问题主要检测学生对知识的理解和掌握程度，检测学生对于学习过的知识能否顺利提取或对刚学过的知识能否准确表述.这种提问类型常见于新授课或复习课.

1.2引导性提问：在学生进行探索分析问题时遇到困难，教师针对学生遇到的困难进行方向性引导性的提问，目的在于指明方向点拨思路.要注意的是这种提问点而不破，问而不答.这种提问类型经常见于习题讲解课中.

1.3过渡性提问：教师在教学中为使一个教学环节向另一个教学环节过渡自然流畅而设置的转折性问题，通常是问而有答直击主题或者是问而不答设置悬念引起学生注意.这种类型的问题一般数量少，应用有限.

1.4系统连贯：问题要按照数学知识的发生发展过程，以相应的数学思想方法为主线，组成一个循序渐进的、具有内部联系的问题体系，系列问题应由易到难层层递进.

2.以例点题，就题论道：以下主要结合实例说明引导性提问的原则与方法.

2.1依图形提问引思路

【例1】设O为坐标原点,过抛物线y2=2px(p>0)焦点F的直线l交抛物线于A,B两点,且|AF|=3|BF|=3,则△OAB的面积为

( )

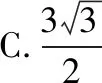
问题1.要求△OAB的面积，该如何选择面积公式？

问题2.如何利用现有的条件求面积？

问题3.能否分割合并求面积？

问题4.图中有弦有焦半径,能否恰当利用此条件(抛物线的定义)？

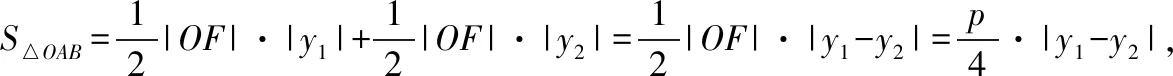
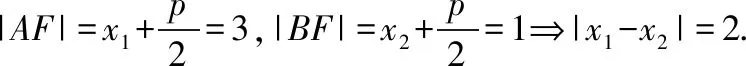
过点B作y轴的平行线，交x轴于点N，过点A作AM⊥BN于点M，抛物线的准线交x轴于点Q.

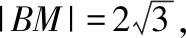
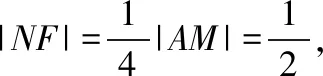
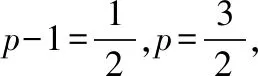
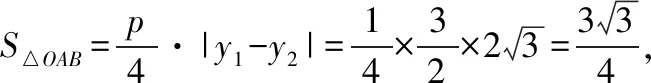
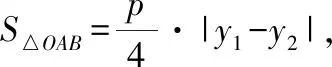
2.2依题型提问点方法

( )

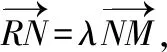
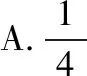
C.1 D.2

问题1.此选择题从正面直接求解思路通畅吗？

问题2.作图分析有哪些量的不确定(任意的)导致其他量的不确定？

问题3.观察选项，选项当中是确定值还是不确定的值？

问题4.选择题的常用解答方法有哪些？

问题5.能否选用特殊化方法？

问题6.该对哪些量或元素特殊化？

问题7.该如何特殊化？

解析：用特殊化方法解答.

令p=2,则抛物线x2=4y,其焦点为F(0,1)，令过焦点F的直线l的方程为y=1，

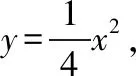
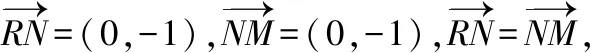
反思：此题从正面直接解答十分繁琐，计算量比较大，而用特殊化方法解答则比较容易.提问的关键在于：首先正确引导学生分析题目中条件，再结合选项的特点想到用特殊化方法；

其次要将抛物线方程具体化，将直线l的位置特殊化；最后还要注意特殊化的目的是为了尽可能的简化计算过程.

2.3依条件提问知深浅

【例3】已知函数f(x)=e2x-a2x-aex,其中e为自然对数的底数,设函数f(x)的导函数为f′(x).

(Ⅰ)试讨论函数f′(x)的单调性;

(Ⅱ)当a>0时，若2e2x-aex≥a2-2a恒成立,求实数a的取值范围.

引导解答(Ⅰ):

问题1.题目求解的是哪个函数的单调性？

问题2.要求其单调性，只需要判定哪个函数的正负？

问题3.判定正负是否涉及参数讨论？

问题4.参数讨论的标准是什么？

解析：因为f(x)=e2x-a2x-aex,x∈R,故f′(x)=2e2x-aex-a2,x∈R.

下面判定f′(x)的单调性,令f′(x)=g(x)，则g′(x)=4e2x-aex=ex(4ex-a),x∈R.

(1)当a≤0时，g′(x)>0恒成立,故f′(x)在R上单调递增;

(2)当a>0时，令g′(x)>0,可得x>lna-2ln2；令g′(x)<0 ,可得x

所以函数f′(x)在(lna-2ln2,+∞)上单调递增,在(-∞,lna-2ln2)上单调递减.

反思：此题是一道高三模拟题，虽然难度不大，但是答题的效果确实不太好，主要原因是绝大多数学生想当然的去求解函数f(x)的单调性，而题目要求解的是函数f′(x)的单调性.教师引导学生解答此题首先要明确题目要求，其次要对参数准确讨论，最后要注意模块化思想及转化化归思想.

2.4依结构提问减运算

下面对例3中(Ⅱ)进行引导解答：

问题1.解答恒成立问题的常用方法有哪几种？

问题2.此题用整体法解答能否进行？

问题3.能否应用(Ⅰ)的结论？

问题4.如何将式子结构转化成(Ⅰ)中的f′(x)？

解析：当a>0时，2e2x-aex≥a2-2a恒成立, 则2e2x-aex-a2≥-2a恒成立.

由(Ⅰ)可知, 当a>0时,f′(x)=2e2x-aex-a2,函数f′(x)在(lna-2ln2,+∞)上单调递增,在(-∞,lna-2ln2)上单调递减.

所以f′(x)≥-2a在x∈R上恒成立，只需满足f′(x)min≥-2a即可.

反思：简化计算过程，提高运算速度与质量，关键在于巧妙利用现有的结论与条件，纵观全局，抓主抓重才可以因势利导，借力打力，达到四两拨千斤的效果.就本题而言,要明确(Ⅰ)的解答是对原题目条件的进一步深度加工，在之后的计算求解中是可以继续应用的；另外还得将(Ⅱ)中的式子结构向(Ⅰ)靠拢.

2.5依要求提问明是非

【例4】《九章算术》是我国的古代数学名著,它在几何学中的研究比西方早一千多年,其中有很多对几何体体积的研究.已知A,B,C均在球O的表面上,且∠AOB=90°,若三棱锥O-ABC的体积V的最大值为36,则当V最大时三棱锥O-ABC的外接球体积为

( )

C.144π D.108π

问题1.作图画球O,三棱锥O-ABC的体积V何时最大？

问题2.三棱锥O-ABC的体积V最大时，三条棱OA,OB,OC之间有什么关系？

问题3.三棱锥O-ABC的外接球是不是球O？

问题4.求解三棱锥的外接球半径的常用方法是什么？

解析：通过作图可知：

三棱锥O-ABC的体积V最大时,OA,OB,OC两两垂直，设球O的半径为R,

则有OA=OB=OC=R,且OA⊥OB,OA⊥OC,OC⊥OB,

设三棱锥O-ABC的外接球半径为r,体积为V′,

反思：在本题的解答过程中,学生很容易错误的将三棱锥O-ABC的外接球理解为球O,因此要顺利引导学生理解球O并不是三棱锥O-ABC的外接球.

2.6依临界提问现思想

【例5】已知圆C:(x-1)2+(y-4)2=10和点M(5,t),若圆C上存在两点A,B使得MA⊥MB,则实数t的取值范围是

( )

A.[-2,6] B.[-3,5]

C.[2,6] D.[3,5]

问题1.点M与圆C的位置关系是什么？点M是否在圆外？

问题2.已知A,B为圆C上两点,当AM,BM为圆C切线时,∠AMB有何特点(最大还是最小)？

问题3.当AM,BM为圆C切线时,点M与圆越近时,∠AMB变大还是变小？

问题4.当AM,BM为圆C切线时,|CM|为何值(临界值)时∠AMB=90°？

问题5.当AM,BM为圆C切线,|CM|减小时,∠AMB是变大还是变小？

问题6.要存在A,B使得∠AMB=90°,|CM|要大于临界值还是小于临界值？

已知A,B为圆C上两点,当AM,BM为圆C切线时,∠AMB最大,

解得t∈[2,6]，故选C.

反思：本题的解答关键在于引导学生体会数形结合思想和运动变化思想.入手点在于临界条件的分析,重点在于理解透彻三条：第一,当AM,BM为圆C切线时,∠AMB最大;第二, |CM|减小时,∠AMB增大;第三,要满足存在性条件,|CM|就要小于等于临界值.

3.总结与展望