核心素养视角下全国卷解析几何命题特点分析

广东 于 涛

自提出核心素养的总体框架和基本内涵以来，高考评价体系就开始经历从能力立意到素养导向的历史性转变，解析几何作为高考重点考查的内容也被赋予了新的含义.结合数学核心素养与2018年《考试说明》来看，2018年全国卷对解析几何的考查，注重基础知识的巩固与理解，主要考查直线与圆锥曲线的基本概念和简单性质，重点考查直线与圆锥曲线的位置关系；注重学科思维的考查，如运动与变化的基本观点和用代数研究几何的基本方法等；强调思想方法的考查，如数形结合、转化与化归、特殊与一般等思想方法；突出两种能力的考查，即逻辑推理能力和运算求解能力；融入了直观想象、数学抽象、数学运算、逻辑推理等数学核心素养.

下面，笔者将结合数学核心素养的命题导向对2018年全国卷解析几何的命题特点进行分析.

1 解析几何命题特点分析

纵观2018年全国卷解析几何的试题编排，试题数量稳定，均为2-3道选填，1道解答，其中选填分布位置稳定，1题属于基础题，1-2题属于中高档题，文理同题比例较往年有所提升.从考查曲线类型来看，4种曲线分布均匀，解答题集中在椭圆或抛物线.

1.1 注重学科基础，凸显直观想象素养

直观想象素养包括借助图形感知认识事物，分析理解问题，通过建立形与数的联系，探索问题的求解思路，也包括数学直觉思维，进行“以图代证”的“正确”猜想.解析几何高考命题注重对基本概念和几何性质等基础知识的考查，如2018年Ⅰ卷文4，Ⅱ卷文6、理5都以基础知识为考查核心.高考命题还强调对基本技能、基本思想和基本活动经验的考查，如2018年Ⅰ卷文15，Ⅲ卷文10在注重“四基”的同时，凸显了直观想象素养.

例1.(2018·全国卷Ⅰ文·15)直线y=x+1与圆x2+y2+2y-3=0交于A，B两点，则|AB|=________．

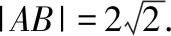
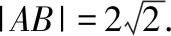
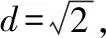
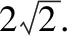
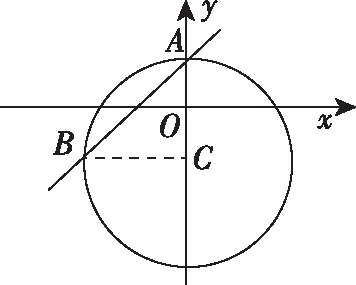
【点评】 试题精心设计了“特殊位置”的直线与圆，使得题目在解答过程中，既可以按照圆锥曲线弦长问题的基本方法求解，又可以结合圆的几何性质求解，还可以借助图形“以图代算”，直接求解，体现了“先画图，再分析、求解”的基本活动经验的重要性，有效地考查了学生的直观想象素养.

1.2 注重学科思维，凸显数学抽象素养

数学抽象素养包括对数量关系与空间形式的抽象概括能力，也包括舍弃事物非本质的属性，揭示其本质属性的思维能力等.解析几何用代数的方法研究图形的几何性质，“代数”是研究工具，“几何”是研究对象，问题的解决始于“几何”，终于“几何”.事实上，“几何”也可以作为研究工具，全面地体现了解析几何的学科思维.如2018年Ⅰ卷理11，Ⅱ卷文11、理12，Ⅲ卷理11都可以从代数、几何两个角度进行问题的求解.几何解法需要经历数学抽象的过程，将题目曲线的基本概念、几何性质等条件信息进行图形化翻译后，抽象出题意蕴含的几何图形，凸显了数学抽象素养.

( )

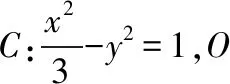
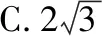
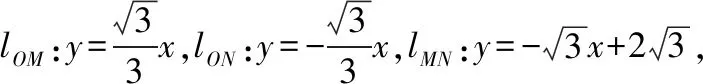
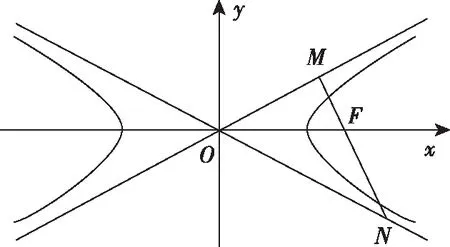
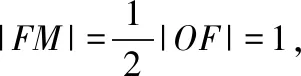
【点评】 试题把直角三角形与双曲线的中心、渐近线有机整合，构建了数形结合的环境，为不同能力的学生提供了方法选择的空间，充分体现了解析几何的学科思维：代数、几何两条路.试题解法的多样性体现了思维的灵活性，代数解法思维量小，运算量大，起点低，落点高；几何解法思维量大，运算量小，起点高，落点低.其中，几何解法从大量信息中抽象出Rt△OMN,Rt△OMF,△OFN三个三角形，极大地简化了运算量.要在“繁杂”的情境中抽象出“简单”的数学对象，需要很好的数学抽象素养.

1.3 强调多想少算，凸显数学运算素养

数学运算素养包括理解运算对象，探究运算思路，选择运算方法，设计运算程序等一系列过程中的思维能力，也包括掌握运算法则，求得运算结果等过程中遇到障碍调整运算的能力，以及敢算的勇气和能算的信心.解析几何试题考查以含字母的式子的运算为主，题目设置平稳，容易上手，注重几何问题解析化，力求人人可算，却不一定能算、巧算.解题时必须进行认真的辨别、探索和选择，做到多想少算，凸显数学运算素养.

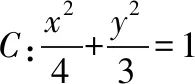
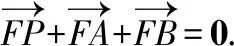
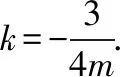
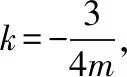
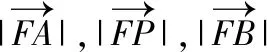
【点评】 试题给定椭圆的方程，创设了椭圆动弦AB的中点在椭圆半通径(x轴上方)上运动的情境.题目第(Ⅰ)问的两个解题思路运算量差别巨大，解答时需要弄清命题背景，选择恰当的运算方法.题目第(Ⅱ)问增加了条件，信息较多，解题时可按照题目条件出现的顺序进行“直译”，以此来理清运算思路.三个环节的运算对象，对运算能力的要求逐步提高，每个环节的计算错误，都会导致后续解答的错误，强调了运算的准确性.试题的两问从不同侧面全面地考查了数学运算素养.

1.4 注重合理转化，凸显逻辑推理素养

逻辑推理素养包括从一些事实和命题出发，推理论证其他命题的思维能力，也包括掌握推理的基本形式和规则，探索和表述论证过程，学会有逻辑地思考问题等.全国卷解析几何试题设问简明扼要，强调对几何条件的等价转化，解题时需根据具体情境广泛地联系相关知识，进行合理转化，探索最佳论证过程.如2018年Ⅰ卷文20、理19，Ⅲ卷文8、理6都需进行合理转化，凸显了逻辑推理素养.

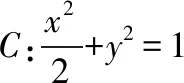
(Ⅰ)当l与x轴垂直时，求直线AM的方程；

(Ⅱ)设O为坐标原点，证明：∠OMA=∠OMB.

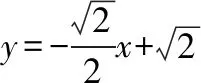
(Ⅱ)要证明∠OMA=∠OMB，需要将其转化为等价的代数关系，设A(xA,yA),B(xB,yB)，如图，联系不同的知识，有如下转化方式.

方式1：由直线MA和直线MB关于x轴对称，得kMA+kMB=0；

方式2：过O作直线MA,MB的垂线，垂足分别为D,E.由OM是∠AMB的角平分线，得dO-lMA=dO-lMB,即|OD|=|OE|；

方式3：记直线MA,MB与y轴的交点分别为G,H.优化方式2，由△OMG≌△OMH，得|OG|=|OH|；

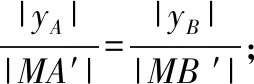
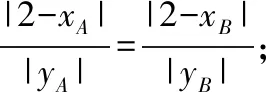
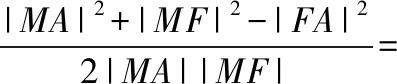
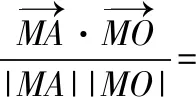
【点评】 试题以动弦(焦点弦)和定点(点M)构造出运动与变化的情景，以图形变化中的几何不变性为命题背景，突出考查了几何问题“解析化”的基本方法.设问的等价转化过程体现了分析法的应用，有效地考查了逻辑推理的基本形式，由形到数的转化体现了数形结合的思想方法，8种转化方式以方式1最佳，方式3，5次之，其余转化方式或运算量巨大，或思路狭窄，多种转化方式的探索与选择，凸显了逻辑推理的思维能力，试题多角度、多层次地考查了逻辑推理素养.

1.5 注重学科规律，凸显探究创新素养

探究创新素养包括发现、提出问题的意识和眼光，综合与灵活运用所学知识、方法的能力，也包括能创造性地解决问题等.解析几何有许多优美的几何性质，高考命题也常以某个性质为背景，或直接应用，或探究证明，注重学科规律，如下表.

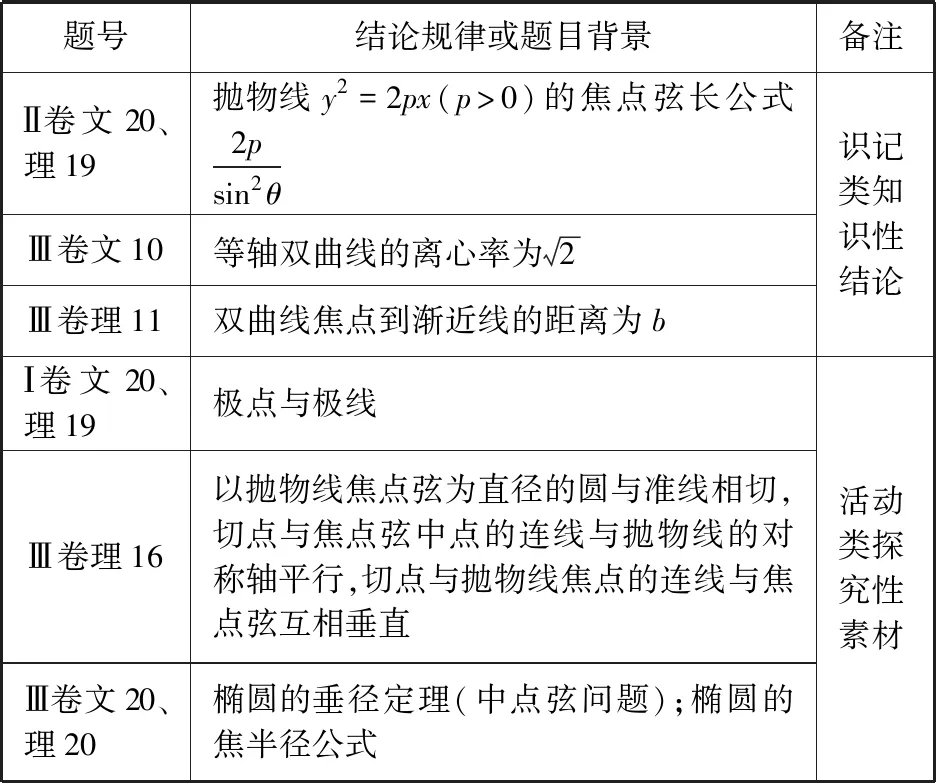
2018年全国卷解析几何试题的结论规律或题目背景

知识性结论的积累和应用，有助于减少解题的运算量.由探究性素材得到或体现的结论，要知其然，知其所以然.教学中可围绕这些问题展开自主探究、合作研究，培养学生发现和提出有意义的数学问题的意识，提升学生猜想合理数学结论的能力，发展学生的探究创新素养.

例5.(2018·全国卷Ⅲ理·16)已知点M(-1,1)和抛物线C:y2=4x，过C的焦点且斜率为k的直线与C交于A,B两点.若∠AMB=90°，则k=________．

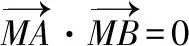
思路2如图，若发现或知道DM∥x轴(D是AB的中点)，则由yA+yB=2yD=2得到关于k的方程.

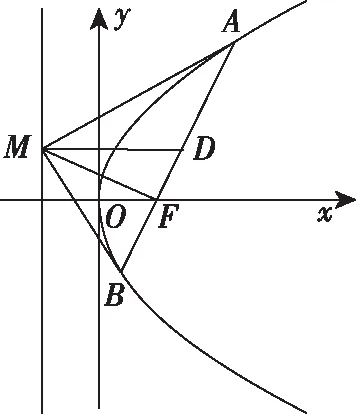
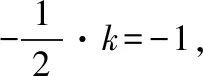
【点评】 试题以抛物线焦点弦的几何性质为命题背景，思路1是常见的解析化思维，运算量很大，间接的从代数角度证明了思路2，3中的结论；思路2，3体现了“几何多一点，代数少一点”的学科思维，根据几何猜想或证明相应结论，凸显了直观想象素养.试题可向教学延伸，进行抛物线平面几何性质的探究，其性质多达十余条(限于篇幅，不一一罗列)，凸显了注重探究创新的命题导向.

2 解析几何复习备考建议

2.1 牢固基础知识

复习备考要用好《考试说明》和教材.《考试说明》能给复习备考以方向性的指导，例如《考试说明》中与圆有关的要求，使用的都是“掌握”“能”这样要求较高的行为动词，因此，要重视对圆的复习，也要重视与圆有关的综合问题的复习，如2018年Ⅱ卷文20、理19就涉及对抛物线与圆的综合考查.关于圆锥曲线的知识要求，则强调概念、性质两手抓，教学时可以帮助学生构建知识体系，积累易错点，力求夯实基础，突出重点.教材是高考命题的素材源泉，复习时可以对教材中的经典例题、习题进行变式、拓展和深化，强化知识的同时，突出对基本技能、基本思想、基本活动经验的复习，扎实学科基础，为素养的养成和发展做好条件准备.

2.2 重视思想方法

数学思想方法引领着数学知识与数学方法的应用，能帮助学生提升思维能力.《考试说明》中与解析几何有关的要求，明确提出：“理解数形结合的思想”，“数”与“形”是解析几何的本质体现，代数好想不好算，几何好算不好想，几何条件挖掘越充分，代数表征就越简洁，运算量就越小，文中例题均有所体现.因此，数形结合不仅要以形助数，更要重视代数、几何两条路，培养学生先几何后代数的思维习惯，力求每个题目都从代数、几何两种角度进行解法研究.全国卷解析几何试题涉及的“几何”多与特殊三角形、相似三角形、解三角形等几何知识有关，教学时可以注重经验的积累.对于其它思想方法，要特别重视转化与化归的思想，教学中对每个几何关系的转化，都要让学生联系所学，尽量多的等价转化，然后再比较不同转化方式的优劣，如文中例4，以此来培养学生形成思维中的惯性观念，以及根据题目条件进行合理转化的能力.除此以外，在有关定值、定点等存在性和探究性问题时，要特别重视特殊与一般的思想，解题从特殊情形入手，先通过“特殊”找到可能存在的结果，再对结果进行一般情形的验证，做到先特殊后一般，四两拨千斤.其中，有关斜率存在与不存在的分类讨论，也可归入特殊与一般的教学.应用思想方法能力的提升，也标志着数学核心素养的发展.

2.3 强化两种能力

逻辑推理能力与运算求解能力是解析几何挣不脱躲不过的能力要求，两种能力并不孤立，逻辑推理能力能帮助学生通过对可行解题思路的预估，评价运算量的大小，引导学生选择运算量较小的解题方式，因此，教学中要注重以逻辑推理助力运算求解.反过来，过硬的运算求解能力，能让学生大胆设取字母，积极运算，能促进学生逻辑推理的畅顺.二者相辅相成，缺一不可，促进逻辑推理素养和数学运算素养的共同提升.

2.4 关注探究创新

素养导向的高考命题以新背景、新情境、新信息等方式，考查学生的科学探究能力和创新能力.教学中要将符合命题导向的高考试题向教学延伸，如文中的例4、例5，不论是对试题多种解法展开探究，还是对试题高等几何背景、抛物线平面几何性质的挖掘与学习，都是激发学生学习兴趣，培养主观能动性，发展创新能力的过程.需要指出，对探究得到的结论或性质，需要让学生明确其证明方法，经历其推导过程，以此来促进学生科学态度的形成，以及科学素养的提升.