立足问题探究 提升思维能力——以一道教材练习题为例谈解题教学

安徽 陈晓明

哈尔莫斯说：“数学的真正组成部分应该是问题和解，解题才是数学的心脏．”波利亚说：“掌握数学就意味着善于解题．”罗增儒教授说：“数学学习中发生数学的地方都无一例外地充满着数学解题活动．”……由此可见，解题教学在数学学习中及其重要．然而，不同教师对解题教学的理解和操作存在很大差别，解题教学现状不容乐观．笔者在此以一道教材练习题为例谈解题教学，解题教学的关键是立足问题探究，提升思维能力．

1.解题教学现状分析

无论是教师还是学生，都感觉高中数学的学习内容深，时间紧，任务重，考试多．学生总感觉数学题目做不完，教师总感觉数学题目讲不完．于是在解题教学的课堂上出现常见的现象是：教师教学方法模式化：“例题+练习”；教学目标单一化：“归题型+列解法”；学生解题范式化：“对题型+套解法”．课堂上教师就题讲题，不停灌输题目的解法，不停按知识点和考点进行“题型”归类，很难涉及解法的发现过程，更谈不上探究题目的数学本质，学生对教师讲解的题目经常是只知其然，而不知其所以然．教师解学生看，学生再模仿训练，在低水平重复操作中达到熟练．

这种灌输讲授加“题海战术”可能短期效益明显，但我们必须承认：这样的解题教学长此以往必将“奴化”学生的思维，学生对解题缺乏自己的思考和认识，甚至没有独立解题的体验，也就不可能真正意义上学会解题．考试时对熟悉的题型可产生本能的反应，但对不熟悉的题型，“无型可套”时很难做到具体问题具体分析，最终把鲜活的、富于挑战性的数学解题智慧沦为以牢固记忆、熟练模仿为主要特征的解题技能．

如此的解题教学，严重违背了我国课程改革的初衷，为了让那些把大量的时间花在无休止的“题海战”上，企图用操练代替创新，以经验积累代替理性思考的考生没有大的作为，高考命题者必然采用反题海战术，多设计一些规避模式化的试题，特别是把关题更是如此．因此，高考加大了探究能力及学习潜能的考查，考查的不是学生会不会套用常见的题型，而是重在考查学生会不会思维，有没有良好的思维习惯，考查的是学生是否有那种探索、求真、质疑的科学精神！这样，没有了教师的“搀扶”，靠“题海战”的学生也就不知所措，无能为力了．

下面笔者以人教A版普通高中课程标准实验教科书数学选修2-1第37页练习第3题为例，研究如何做到立足问题探究，提升思维能力，让我们的解题教学落到实处．

2.教学案例

教师：在前面的学习和作业中同学们出现了这样那样的错误，感觉在求曲线方程时困难较大．今天我们来探究教材第37页练习第3题，以此来研究求轨迹方程的一般方法，看看此类问题难点在哪儿，以及我们如何突破．

问题如图，已知点C的坐标是(2,2)，过点C的直线CA与x轴交于点A，过点C且与直线CA垂直的直线CB与y轴交于点B．设点M是线段AB的中点，求点M的轨迹方程．

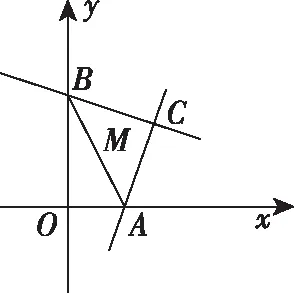
这个问题起点低，所有学生都可参与探究．学生可以从问题的多元表征去探究，形成问题解决的不同思路，培养思维的分散性、灵活性、广阔性与深刻性，从而提升思维能力．

让学生充分思考并理清自己的思路后开始交流、展示．由学生分析思路并给出解法，教师引导反思．

学生1：要求M点坐标，需要知道A，B两点坐标，而这两点坐标都不知道，于是我想到设出A点坐标(含参)，然后求出B点坐标(含同样的参数)，再利用中点坐标公式消去参数．这样问题的关键转化为求B点坐标，而只要求出直线CB的方程即可(令x=0)，又直线CB过定点C(2,2)，因此只需求直线CB的斜率，因为CA⊥CB，所以只需求直线CA的斜率，而A点坐标已设出，问题就迎刃而解了．

解法1(参数法)：设点A,M的坐标分别为(t,0)，(x,y)．

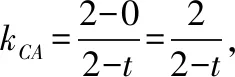
(2)当t=2时，可得点A，B的坐标分别为(2,0)，(0,2)，此时点M的坐标为(1,1)，它仍然适合方程③．

由(1)(2)可知，方程③是点M的轨迹方程，它表示一条直线．

教师：分析地很有道理，一步步顺藤摸瓜，我们解题需要这样的良好思维习惯．而且注意到了分类讨论，很好．

学生2：我没有引进参数，直接设出M点坐标，利用中点坐标公式求出A，B两点坐标(用M点坐标表示)，然后求出直线CA和CB的斜率，利用CA⊥CB得到它们斜率的等量关系，从而得到方程．

解法2(直接法)：设点M的坐标为(x,y)．

(1)当直线CA的斜率存在时,

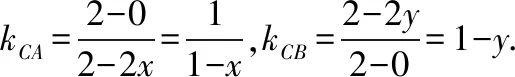
(2)当直线CA的斜率不存在时，

易求点A，B的坐标分别为(2,0)，(0,2)，此时点M的坐标为(1,1)，它仍然适合方程③．

由(1)(2)可知，方程③是点M的轨迹方程，它表示一条直线．

教师：不引进参数也能解决问题，真聪明！大家比较一下这两种方法，看看有什么异同点？

学生3：两种方法本质相同，都用到了中点坐标公式；都利用题中关键条件CA⊥CB，将几何条件代数化；都考虑到了斜率的存在性，进行分类讨论．只不过前者含参，后者不含；前者用A，B两点坐标表示M点坐标，后者用M点坐标表示A，B两点坐标；前者由垂直关系得斜率关系，得直线方程求坐标；后者由垂直关系得斜率关系，由等量关系直接得轨迹方程．从计算量等方面来说直接法更简洁些．

教师：比较得很彻底．我们解题要抓住题目的本质．

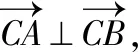
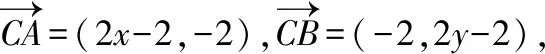
教师：很好，把垂直关系用向量形式表示，进一步用坐标表示，几何条件代数化，解答变得简洁，而且避免了分类讨论．

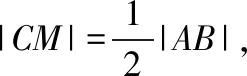
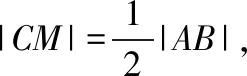
教师：厉害！没想到几何法也能解决轨迹问题，数形结合思想真是重要，而且也不需分类讨论．

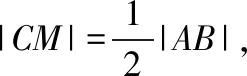
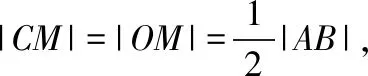
教师：真是“条条大道通罗马”！这种解法利用等量代换，还避免了求点A，B的坐标．

学生8：我由前面两位同学的解法受到启发，发现O,A,C,B四点共圆，于是我想到先设出圆的方程，利用半径为|OM|，点C(2,2)在圆上解决问题．

解法6(解析法)：设点M的坐标为(a,b)，因为CA⊥CB，OA⊥OB，所以O,A,C,B四点共圆，圆心为点M，半径为|OM|，因此令圆M的方程为(x-a)2+(y-b)2=a2+b2，又点C(2,2)在圆上，把点C坐标代入圆的方程可得(2-a)2+(2-b)2=a2+b2，化简得a+b-2=0，即点M的轨迹方程为x+y-2=0．

教师：不难看出，解法6与解法5本质相同，但视角不同，数学之间的联系真是奥妙无穷．另外，O,A,C,B四点共圆对于图中点A，B分别在x轴，y轴正半轴成立，其他情况就不成立了，这一点应引起注意．

在不知不觉中课堂学习氛围变得十分热烈，这时一位一向比较内敛的同学举手了，可能是被课堂气氛感染了，笔者立即给他说话的机会．

学生9：我也是用M点坐标表示A，B两点坐标，但我没有利用直角三角形的中线性质，而是直接在Rt△ABC中利用勾股定理．

解法7(几何法)：设点M的坐标为(x,y)，由中点坐标公式易得A(2x,0)，B(0,2y)，又C(2,2)，所以|CA|2=(2x-2)2+4，|CB|2=4+(2y-2)2，|AB|2=4x2+4y2．因为CA⊥CB，所以△ABC为直角三角形，由勾股定理得|CA|2+|CB|2=|AB|2，所以(2x-2)2+4+4+(2y-2)2=4x2+4y2，进一步可化为x+y-2=0 ③．

教师：很好，原来几何法有这么多表现形式．集体的智慧真是不可限量！想出了这么多方法，接下来大家比较一下这些方法，总结一下求轨迹方程的方法．

学生10：参数法是观察轨迹的形成过程，选择恰当的参数描述动点坐标所适合的等量关系，消参化为普通方程．所以说参数法是一种通法，参数由问题背景确定．

学生11：向量法在本质上属于直接法，都是将几何条件代数化，只是转化的途径不同，有时用向量法要简洁些，可能避免了分类讨论．

学生12：几何法在本质上也属于直接法，只不过对几何条件采取了不同的表现形式，能让我们看到问题的本质而已．

教师：大家总结地很好，尽管求轨迹的方法很多，但有些方法在本质上是相同的．虽然思考问题的视角不同，就像本题对关键条件CA⊥CB的处理方式不同，但最终目标是一致的，即求动点坐标之间的关系(方程)．请同学们接下来思考教材中本页习题第4题，看看该如何解决？

变式(人教A版普通高中课程标准实验教科书数学选修2-1第37页习题第4题)：

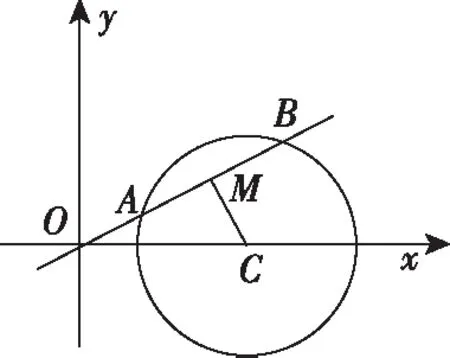
过原点的直线与圆x2+y2-6x+5=0相交于A，B两点，求弦AB的中点M的轨迹方程．

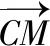
3.教学反思

本课例以自主探究活动为载体，以贴近学生“最近发展区”的轨迹问题为支点，在探究、变式中，使学生的解题能力与思维能力同步提升．解题教学要选择适宜的问题，学生“跳一跳，够得着”的问题，而且问题具有分散性，即解决问题方法的多样性和条件或结论的可变性．有了问题学生就有了思考与讨论的方向，从而能持续地驱动学生进行探究，激发思维．另外，解题教学中，解题后教师要引导学生对解题方法进行分析、评价，从而培养学生的思维能力．

在解题教学中,有些教师一堂课能讲很多题目，有些题目点到为止，其“含金量”会有多少？因为学生缺少了各种体验的机会，没有了比较分析，一旦遇到了不同的问题，当然不会随机应变，因此考场上经常出现教师讲过的题学生仍然不会做的现象就不足为奇了．课堂上教师、学生都花了时间，却没得到相应的效果，得不偿失．所以，草草讲10道题，不如讲透1道题，解题教学要讲究质量．