解析几何重难点题型解析

福建 陈荣桂

解析几何是高中数学的重要内容，在历年的高考中占据了重要的位置.几年来，无论是选择题、填空题还是解答题的考查，都有一定的难度，综合考查了学生的抽象概括能力、运算求解能力、数据处理能力等数学能力，体现了数学抽象、逻辑推理、数学运算、数据处理等数学核心素养，具有较好的区分度．

一、圆锥曲线定义的考查

( )

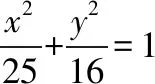
A.0个 B.1个

C.2个 D.4个

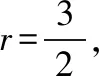
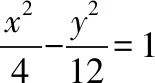
【解析】设双曲线的右焦点为F1，|PF|+|PA|=2a+|PF1|+|PA|≥2a+|AF|=4+5=9．

【例3】(2009·四川卷理·9)已知直线l1:4x-3y+6=0和直线l2:x=-1，抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是

( )

A.2 B.3

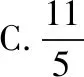
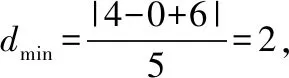
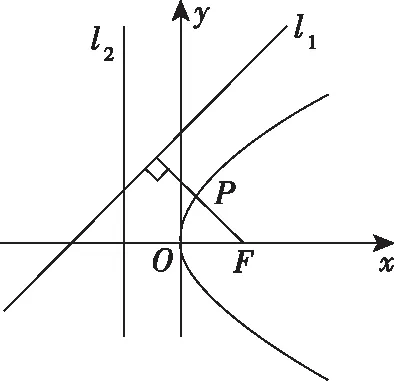
【评注】在解析几何问题中，利用定义解题可以简化运算，通过化归与转化、数形结合等思想方法的运用，简单快速地解决问题.

二、圆锥曲线的几何性质

( )

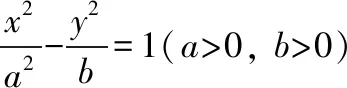
A.(0,2) B.(1,3]

C.[2,3) D.[3,+∞)

【解析】由定义知|PF1|-|PF2|=2a,所以|PF1|=2a+|PF2|，

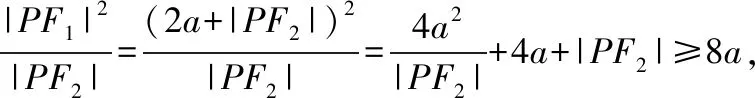
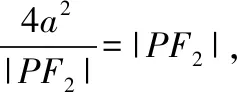
因为|PF2|≥c-a，所以c-a≤2a，即c≤3a，e≤3．

又双曲线的离心率e>1,所以e∈(1,3]，故选B．

( )

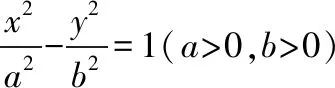
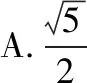
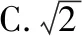
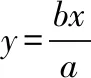
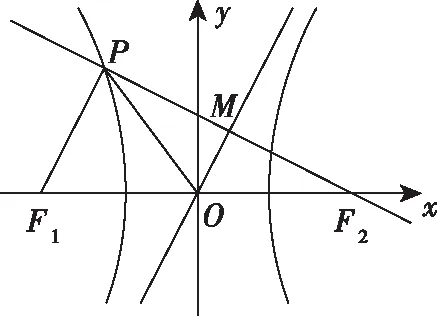
【评注】在解析几何问题中，椭圆、双曲线、抛物线的几何性质的合理运用，可将问题转化为几何问题，常可直接利用几何意义求解.

三、直线与圆锥曲线的位置关系

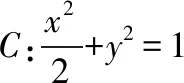
(Ⅰ)当l与x轴垂直时，求直线AM的方程；

(Ⅱ)设O为坐标原点，证明：∠OMA=∠OMB.

【解析】(Ⅰ)由已知得F(1,0)，当l与x轴垂直时l的方程为x=1.

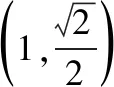
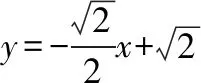
(Ⅱ)当l与x轴重合时，∠OMA=∠OMB=0°；

当l与x轴垂直时，OM为AB的垂直平分线，所以∠OMA=∠OMB；

当l与x轴不重合也不垂直时，设l的方程为y=k(x-1)(k≠0)，A(x1,y1),B(x2,y2)，

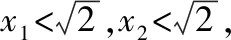
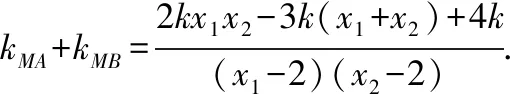
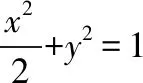
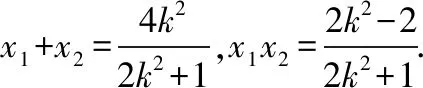
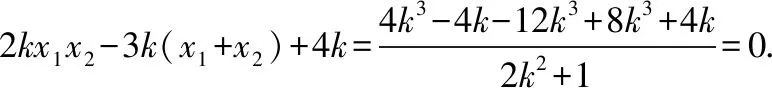
从而kMA+kMB=0，故直线MA，MB的倾斜角互补，所以∠OMA=∠OMB.

综上，∠OMA=∠OMB.

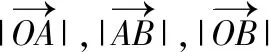
(Ⅰ)求双曲线的离心率；

(Ⅱ)设AB被双曲线所截得的线段长为4，求双曲线的方程．

【解析】(Ⅰ)设|OA|=m-d,|AB|=m,|OB|=m+d,

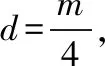
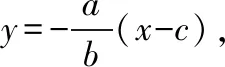
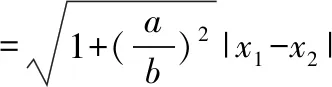
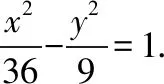
【评注】直线与圆锥曲线的位置关系是高考解析几何考查的永恒的主题，学习中必须掌握位置关系的判断及相关问题(如弦长、中点弦等)的常见题型的解法，切实提高运算的准确性．

四、平面向量在圆锥曲线问题中的应用

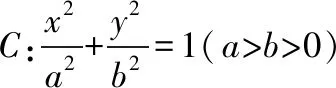
(Ⅰ)证明：线段AB的中点为定点，并求出该定点坐标；

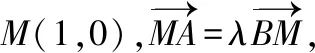
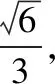
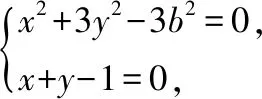
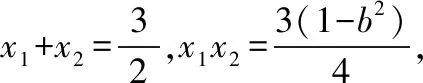
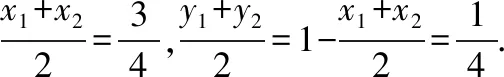
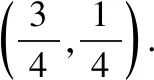
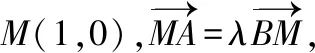
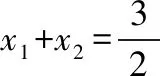
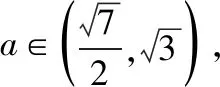
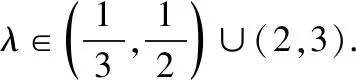
【评注】利用平面向量知识解决圆锥曲线问题，可以减少部分运算量，使问题更容易解决．常见的题型有利用向量求角度问题、定比分点问题、证明垂直平行问题等．

五、圆锥曲线的最值(取值范围)问题

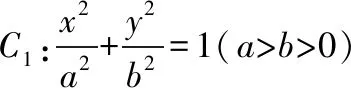
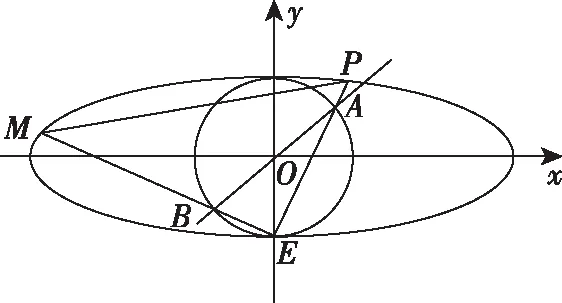
(Ⅰ)求椭圆C1的方程；

(Ⅱ)求△EPM面积的最大值．

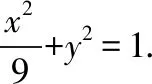
(Ⅱ)由题意得直线PE,ME的斜率存在且不为0，PE⊥EM，不妨设直线PE的斜率为k(k>0)，则直线PE的方程为y=kx-1，

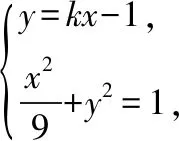
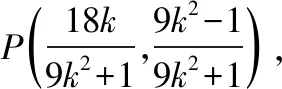
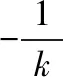
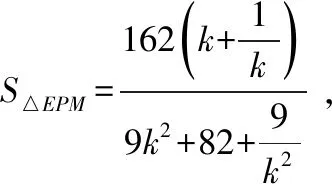
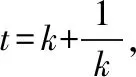
【评注】求最值或求范围问题，常见的解法有三种：

(1)几何法：若题目的条件和结论能明显体现几何特征及意义，则考虑利用图形性质来解决；

(2)函数法：若题目的条件和结论能体现一种明确的函数关系，则可首先建立目标函数，再求这个函数的最值．

(3)不等式法：若题目的条件有不等关系，可构造不等式(组)求解．

六、圆锥曲线的定值问题

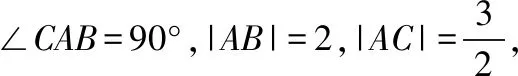
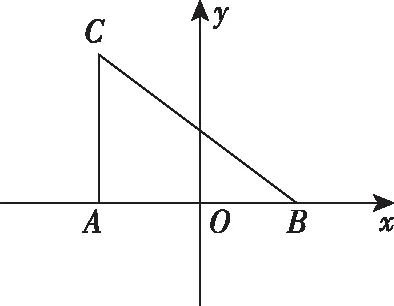
(Ⅰ)求曲线E的方程；

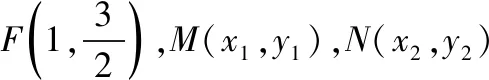
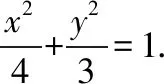
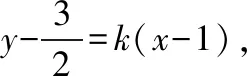
消元得(3+4k2)x2-4k(2k-3)x+(4k2-12k-3)=0，

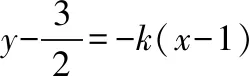
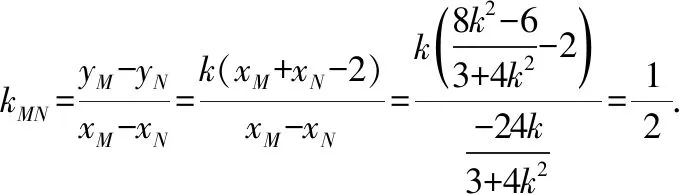
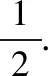
【评注】求定值问题常见的方法有两种：

(1)从特殊情况入手，求出定值，再证明这个值与变量无关．

(2)直接推理、计算，并在计算推理的过程中消去变量，从而得到定值．

七、定点的探索问题

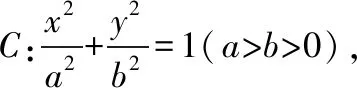
(Ⅰ)求C的方程；

(Ⅱ)设直线l不经过P2点且与C相交于A，B两点，若直线P2A与直线P2B的斜率的和为-1，证明：l过定点．

【解析】(Ⅰ)根据椭圆对称性知椭圆C必过P3，P4，又P4横坐标为1，椭圆C必不过P1，所以椭圆C过P2，P3，P4三点．

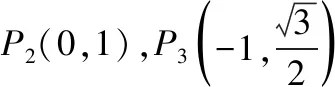
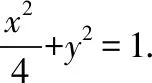
(Ⅱ)证明：①当直线l斜率不存在时，设l:x=m，A(m，yA)，B(m，-yA)，

得m=2，此时l过椭圆右顶点，不存在两个交点，故不满足．

②当直线l斜率存在时，设l∶y=kx+m(m≠1)，

A(x1，y1)，B(x2，y2)，

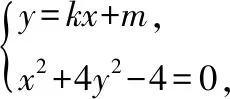
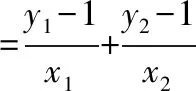
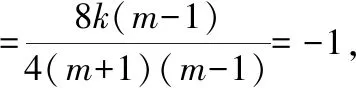
则m=-2k-1，此时Δ=-64k，存在k使得Δ>0成立．

所以直线l的方程为y=kx-2k-1，

当x=2时，y=-1，所以l过定点(2，-1)．

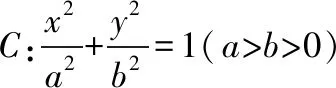
(Ⅰ)求椭圆C的标准方程；

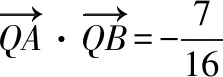
【解析】(Ⅰ)由题意知c=1.

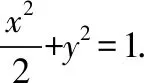
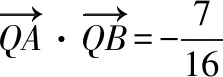
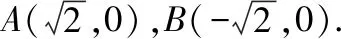
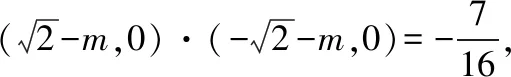
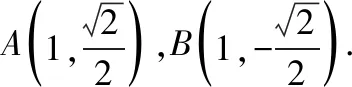
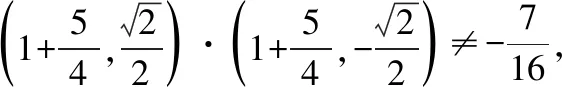
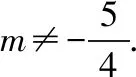
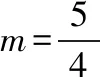
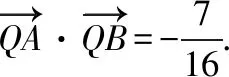
当直线l的斜率不为0时，设直线l的方程为x=ty+1，A(x1,y1),B(x2,y2).

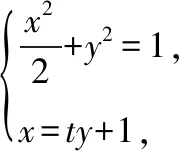
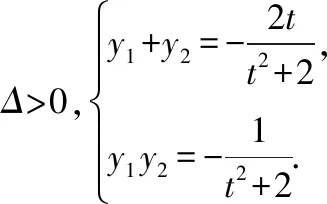
因为x1=ty1+1，x2=ty2+1，

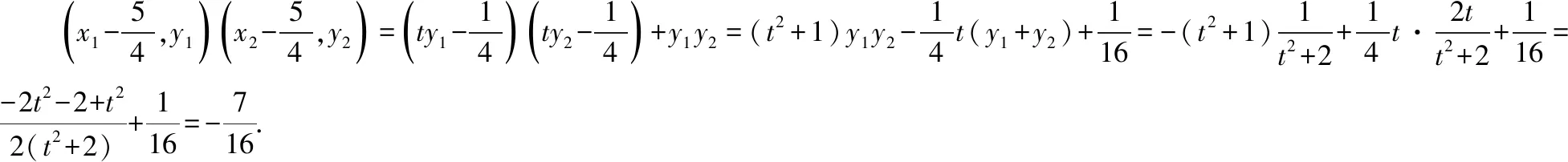
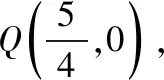
【评注】解决定点的探索与证明问题，一般有以下两种方法：

(1)探索直线过定点时，可设出直线方程为y=kx+m，然后利用条件建立k,m的等量关系进行消元，借助于直线系的思想找出定点．