全国卷Ⅰ三角函数相关考点探究

湖北 廖庆伟

三角函数是高中数学中非常重要的组成部分，此部分知识是对前面函数知识的延伸，也是对三角形知识的拓展，属于高考中的热点.因此在学习及备考中，要抓住三角函数的本质，把握好三角恒等变换的方向，进而提高三角函数复习的备考质量.

近三年全国卷Ⅰ中三角函数及解三角形回顾：

从知识点上看：三角函数的定义、诱导公式、同角三角函数间的关系、三角恒等变换、三角函数的性质(单调性、奇偶性、周期性、最值等)、三角函数的图象变换、正弦定理、余弦定理、三角形的面积公式均有考查.

从题型上看：文科一般考查三个小题，分值15分；理科一般考查一大一小，分值17分，题目形式灵活多样.

从难度上看：三角函数与解三角形是高考考查的重点，高考题中逐渐抛弃了对复杂的三角恒变换和特殊技巧的考查，重点转移到利用三角函数公式进行恒等变换、三角函数的性质与图象变换等方面.重视对基础知识、基本技能的考查，属中等题或容易题.

【考点焦聚一】三角函数定义

知识点：直线的斜率、三角函数的概念与性质、二倍角的余弦公式.

解题路径：首先根据两点都在角的终边上，得到a，b的关系式，利用倍角公式以及余弦函数的定义式，求得a2，从而得到|a|，再结合a，b的关系，从而得到a-b的值，进而确定选项.

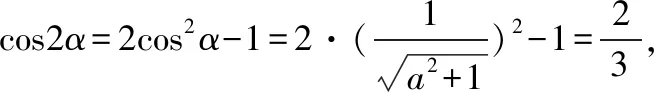
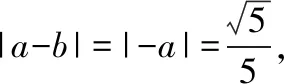
易错点：记错二倍角的余弦公式、三角函数的定义公式.

【考点焦聚二】三角函数的最值

例2.(2018·全国卷Ⅰ文·8)已知函数fx=2cos2x-sin2x+2，则( )

A.f(x)的最小正周期为π，最大值为3

B.f(x)的最小正周期为π，最大值为4

C.f(x)的最小正周期为2π，最大值为3

D.f(x)的最小正周期为2π，最大值为4

知识点：三角函数的性质

解题路径：首先利用二倍角公式，对函数解析式进行化简，应用余弦函数的性质得到相关的量，从而得到正确选项.

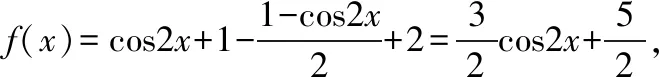
易错点：该题考查的是用二倍角的余弦公式化简三角函数解析式，并且通过余弦函数的相关性质得到函数的性质，在解题的过程中，要注意应用倍角公式将式子降次升角，得到最简结果.

【考点焦聚三】三角函数的图象与性质

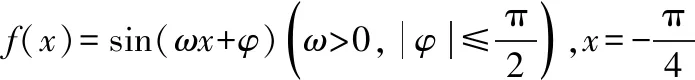
A.11 B.9 C.7 D.5

知识点：正弦函数的图象与性质、函数的零点.

解题路径：根据已知条件求ω的范围，讨论当ω=11、ω=9时是否满足条件，确定正确选项.

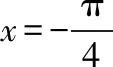
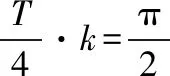
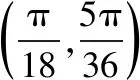
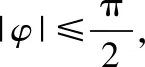
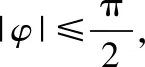
所以ω的最大值为9，故选B.

易错点：判断函数f(x)的周期出错，注意fx=Asinωx+φA≠0,ω≠0的单调区间长度是半个周期；若fx=Asinωx+φA≠0,ω≠0的图象关于直线x=x0对称,则fx0=A或fx0=-A.

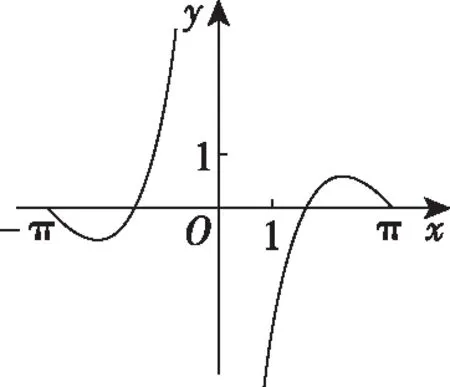
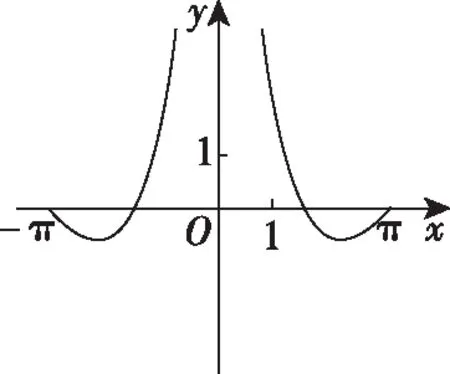
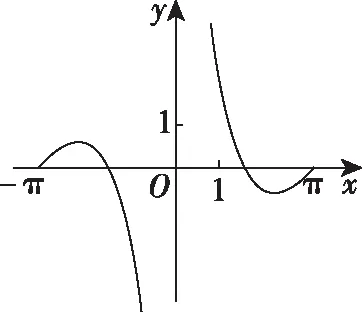
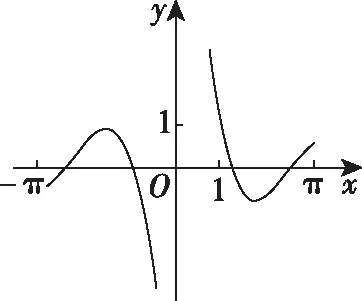
知识点：三角函数的图象与性质.

解题路径：先判断函数的奇偶性，再取x=π，x=1代入解析式验证，从而确定正确的选项.

当x=π时，y=0，故排除D；

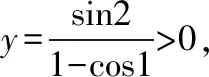
故选C.

易错点：看图不仔细、不能灵活利用估算法求解数学问题.

【考点焦聚四】三角恒等变换

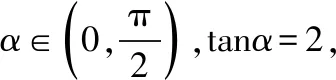
知识点：同角三角函数关系、两角差的余弦公式.

解题路径：由同角三角函数间的关系求出cosα，sinα，再根据两角差的余弦公式及特殊角的三角函数值求结论.

解析：由tanα=2得sinα=2cosα，

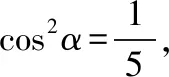
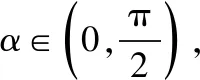
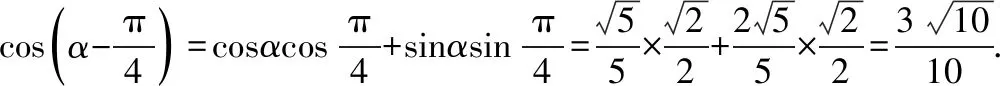
易错点：记错两角差的余弦公式和特殊角的三角函数值的符号.

【考点焦聚五】正弦定理

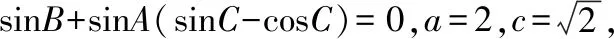
知识点：三角形内角和定理、两角和的正弦公式、正弦定理.

解题路径：由三角形内角和定理、两角和的正弦公式求角A，再由正弦定理求sinC，根据三角形的性质确定角C的大小.

解析：由题知sin(A+C)+sinA(sinC-cosC)=0，

所以sinAcosC+cosAsinC+sinAsinC-sinAcosC=0，

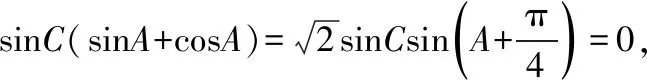
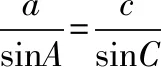
因为c

易错点：记错三角函数公式、忽视三角形中大边对大角.

【考点焦聚六】余弦定理

知识点：余弦定理.

解题路径：由余弦定理求结论.

易错点：根据余弦定理整理出关于b的一元二次方程,再通过解方程求b.运算失误是基础题失分的主要原因.

【考点焦聚七】解三角形

例8.(2018年·全国卷Ⅰ文·16)△ABC的内角A，B，C的对边分别为a，b，c.已知bsinC+csinB=4asinBsinC，b2+c2-a2=8，则△ABC的面积为________.

知识点：解三角形、三角形的面积.

解题路径：首先利用正弦定理及题中的式子化简求得sinA，利用余弦定理，结合题中的条件，可以得到A为锐角，从而求得cosA，进一步求得bc，利用三角形面积公式求得结果.

解析：根据题意，结合正弦定理可得sinBsinC+sinCsinB=4sinAsinBsinC，因为sinB≠0，sinC≠0，

因为b2+c2-a2=8，所以2bccosA=8，

易错点：忽视隐含条件判断角A为锐角.

例9.(2018·全国卷Ⅰ理·17)在平面四边形ABCD中，∠ADC=90°，∠A=45°，AB=2，BD=5.

(Ⅰ)求cos∠ADB；

知识点：正弦定理、余弦定理、同角三角函数关系.

解题路径：(Ⅰ)根据正弦定理、题设条件，求得sin∠ADB，结合角的范围，利用同角三角函数关系式，求得cos∠ADB；(Ⅱ)根据题设条件以及第一问的结论可以求得cos∠BDC，sin∠ADB，之后在△BCD中，用余弦定理得到BC所满足的关系，从而求得结果.

由题设知，∠ADB<90°，

所以BC=5.

易错点：不能根据题目条件灵活运用正弦定理、余弦定理，对角∠ADB的范围判断出错.