一道解三角形实际应用题的原创之旅
贵州 袁小勇
笔者有幸参加由《教学考试》杂志社主办的方向五二轮复习测评项目,从2018年8月1日开始组建团队,到2018年8月30日结束,历经1个月时间,收获颇丰,首先是收获了团队“原创·研发”的开拓精神,即原创理念引领,团队通力合作,把脉高考.其次是老师们在参与“原创·研发”活动的过程中相互学习、借鉴,不仅收获了友谊,也使自身的能力得到大幅度地提高.
本阶段“原创·研发”的任务是根据杂志社提供的双向细目表命制一套二轮复习试卷.在本套试卷中16题的考点为解三角形,一级考向为解三角形实际应用举例,二级考向为中间有障碍或不可达到的两点距离、不可直接测量的三角形角度问题.笔者在准备阶段找不到较好的背景,并且思维量和难度达不到压轴题的要求.通过团队协作讨论,可以先不考虑试题背景以及局限于在三角形内解决问题.可以先确定要考查的数学思想和数学核心素养,找出与其他知识的联系,再回到三角形中解决问题,我们以一个定点到圆(或圆弧)上一动点距离的最值为基本考点,再转化到三角形中利用正、余弦定理求线段长度,最后再寻找符合题意的实际背景,即得到一稿试题如下:
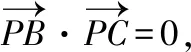
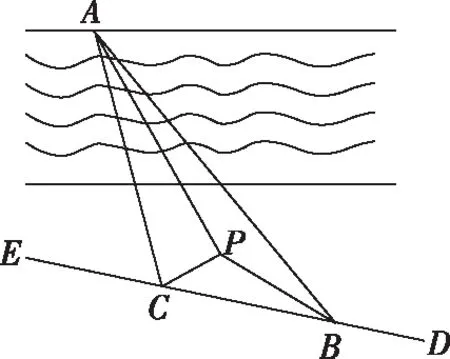
【命题意图】本题考查正弦定理、余弦定理的实际应用;考查运算求解、转化与化归能力;考查数学建模、数学运算核心素养.
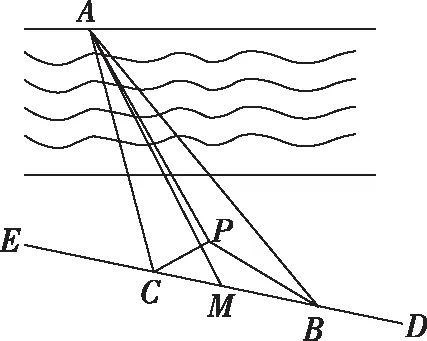
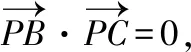
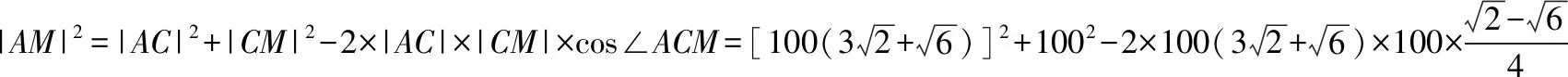
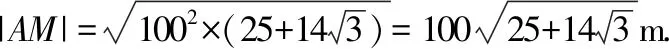
在一稿试题中,为了使题干中的角度特殊化,得到的结果比较繁琐,为让计算结果不含二层根式,尝试改变题干中的角度.但若随意更改,计算会更加复杂,所以我们得抓住问题的本质,再尝试更改.而本题的核心是在△ABC中,M为CB的中点,已知△ABC中的一些角度,求AM的长.
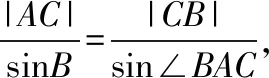
【尝试二】固定角A,改变角B,结合一稿试题,不妨设∠BAC=45°,|BC|=x,

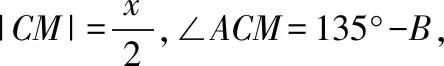
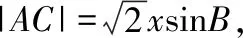
在△ACM中,由余弦定理可知,
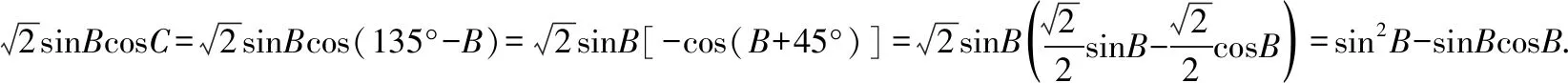
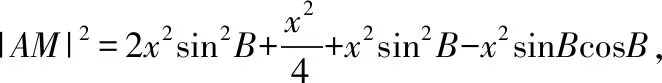
所以,要使得|AM|的长不含二层根号,只需保证sin2B,sinBcosB均为有理式即可.所取角度尽量让学生熟悉,所以取B=37°(sin37°可近似取为0.6),即得到定稿试题如下:
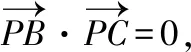

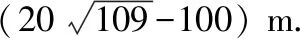
【命题意图】本题考查正弦定理、余弦定理的实际应用;考查运算求解、转化与化归能力;考查数学建模、数学运算核心素养.
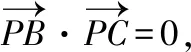
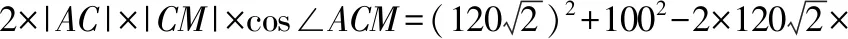
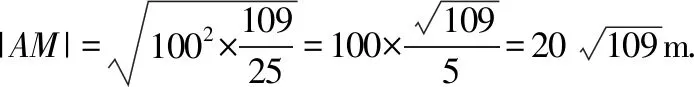

——记我的原创感悟

